一些问答

1.Convolution: Translationally Invariant Quasilocal Unitaries 理解？

• Convolution（卷积）：
  在量子信息或量子多体系统中，"卷积"通常指一种分层、局部操作的结构，类似于经典卷积神经网络中的局部滤波器。其特点是通过重复的局部操作组合成全局变换，同时保持某种对称性（如平移不变性）。

• Translationally Invariant（平移不变性）：
  系统在空间平移后性质保持不变。例如，在一维链状量子系统中，每个位置的局部门完全相同，且排列周期性重复。

• Quasilocal（准局域）：
  操作的影响范围有限但非严格局域。例如，一个门的作用可能涉及相邻的多个粒子（如最近邻或次近邻），但随距离衰减迅速，不涉及整个系统。

• Unitary（酉操作）：
  量子力学中的幺正变换，保证演化过程的内积守恒（即概率守恒），对应可逆的量子逻辑门。

• 特性	严格局域操作	准局域操作
  作用范围	严格限制在有限区域（如最近邻）	影响范围有限但可延伸（如次近邻）
  衰减速度	突跃式截断（零作用超出范围）	随距离指数衰减（非零但快速减小）
  应用场景	精确控制的小系统	大系统近似模拟或容错计算

2. 无限系统尺寸密度矩阵重整化群（DMRG）与量子卷积神经网络（QCNN）的相图？

• Phase diagram（相图）：描述物质或量子系统在不同参数（如温度、磁场）下的相态分布。

• DMRG（密度矩阵重整化群）：一种用于研究一维量子多体系统的数值方法，擅长处理强关联效应。

• QCNN（量子卷积神经网络）：结合量子计算与深度学习的模型，常用于量子态分类或特征提取。

3.String Order Parameter（弦序参量）?

        String Order Parameter（弦序参量） 是一种用于表征拓扑有序系统或对称性保护拓扑相（SPT）的非局域序参量。与传统局域序参量（如磁化强度）不同，弦序参量通过测量系统中沿一维路径的算符关联性，反映系统的长程量子纠缠或拓扑性质。

• 非局域性：依赖路径上所有自旋的关联，而非局部对称性破缺。

• 对称性保护：弦序参量的非零值依赖于系统对称性（如时间反演对称性、晶格平移对称性）。

• 拓扑区分：能够区分拓扑平凡相（如Neel相）与非平凡相（如Haldane相）。

• 

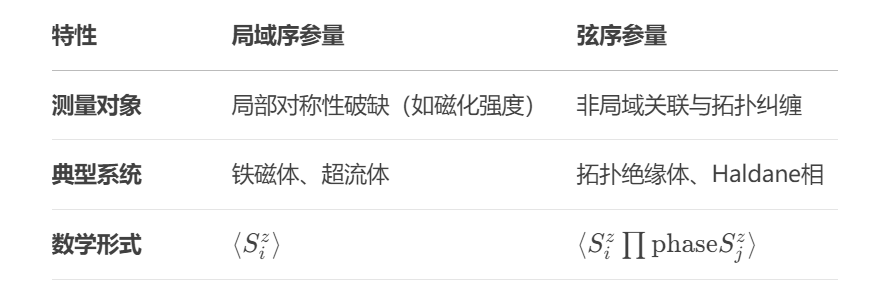
4.解释图片？

答：

5.解释QCNN = MERA + QEC

1. 多尺度纠缠（Multiscale Entanglement）：
   描述量子系统中不同空间或能量尺度上的纠缠结构，常见于量子多体态（如拓扑态）的分析。

2. QCNN（Quantum Convolutional Neural Network）：
   量子卷积神经网络，通过局部滤波和分层结构提取量子态的多尺度特征。

3. MERA（Multiscale Entanglement Renormalization Ansatz）：
   一种张量网络表示方法，用于高效描述具有层级纠缠结构的量子态（如临界系统）。

4. QEC（Quantum Error Correction）：
   量子纠错技术，通过冗余编码保护量子信息免受噪声干扰，依赖纠缠资源（如表面码）。

6.经典纠错和量子纠错？

经典与量子纠错的对比

特性	经典纠错	量子纠错
信息冗余	重复物理比特（如000）	逻辑态分布于多个纠缠物理比特
错误类型	比特翻转（0↔1）	比特翻转（�X）、相位翻转（�Z）
核心限制	无物理限制	不可克隆定理、退相干效应
典型编码	重复码、海明码	表面码（Surface Code）、肖尔码

---

总结

量子纠错通过稳定子测量和逻辑态编码，在遵守量子力学基本限制的前提下实现容错计算，是构建大规模量子计算机的核心技术。其复杂性远超经典纠错，但为量子计算的可靠性和可扩展性奠定了基础。