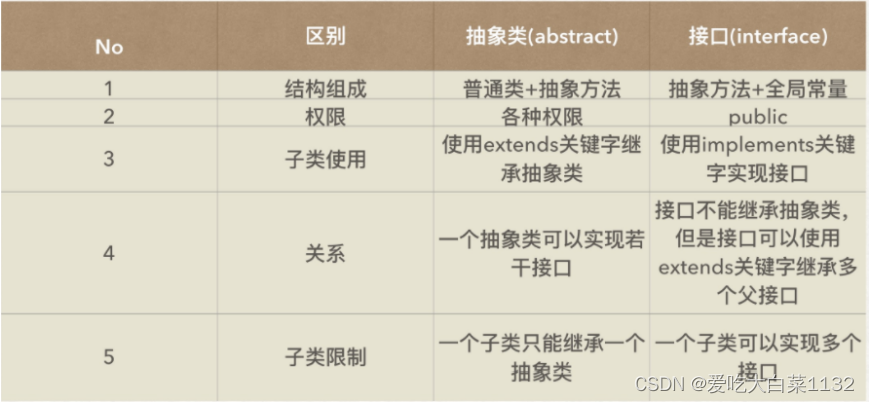
排序算法总结
- 插入排序
- 直接插入排序(稳定)
- 希尔排序
- 交换排序
- 冒泡排序(稳定)
- 快速排序
- 选择排序
- 简单选择排序
- 堆排序
- 归并排序(稳定)
- 基数排序(稳定)
- 多路归并排序(外排序)
- 总结
- 知识点总结
- 题目总结
复习自用
插入排序
直接插入排序(稳定)
将待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,就得到一个新的序列。(抓扑克牌思想)
特点:元素越接近有序,直接插入排序算法的时间效率越高,算法的本质是减治算法;因此当数组接近有序或大概率有序的情况下,或是数组的数量比较小的时候采用插入排序。
时间复杂度:
最好情况:(有序且为正序)O(n)
最坏情况:(逆序)O(n^2)
平均情况:O(n2)
空间复杂度:O(1)
具有稳定性
希尔排序
先将数据进行分组,通过插入排序的方式让数据基本有序,然乎再进行插入排序,能够让插入排序最坏情况的概率降低;
分组的方法:固定步长取值分为一组的方法。分组越多(步长越小)大的数往后走的越快,分组越少排完后越接近有序
希尔排序是对直接插入排序的优化
时间复杂度:
最好情况(正序):O(n)
平均情况:O(n1.3–n2)
最坏情况(逆序):O(n2)
空间复杂度:O(1)
不具有稳定性的排序
交换排序
冒泡排序(稳定)
根据序列中两个记录的值的比较结构来交换两个记录在序列中的位置,将值较小的向前移动
特点:算法的本质是减治排序
时间复杂度:
最好情况(正序):O(n)
最坏情况(逆序):O(n2)
平均情况:O(n2)
空间复杂度:O(1)
稳定性:稳定
快速排序
一共包含三大步:
1.确定待排序元素序列中的某元素作为基准值(选区间最右边的元素/选中间元素 与最右边的元素交换)
2.以基准值为界,大于基准值的放在基准值的右边,小于基准值的放在基准值左边(hover 挖坑 前后下标)
3.然后对左右序列重复该过程,直到小区间中只有一个元素或没有元素为止(size==0||size ==1)
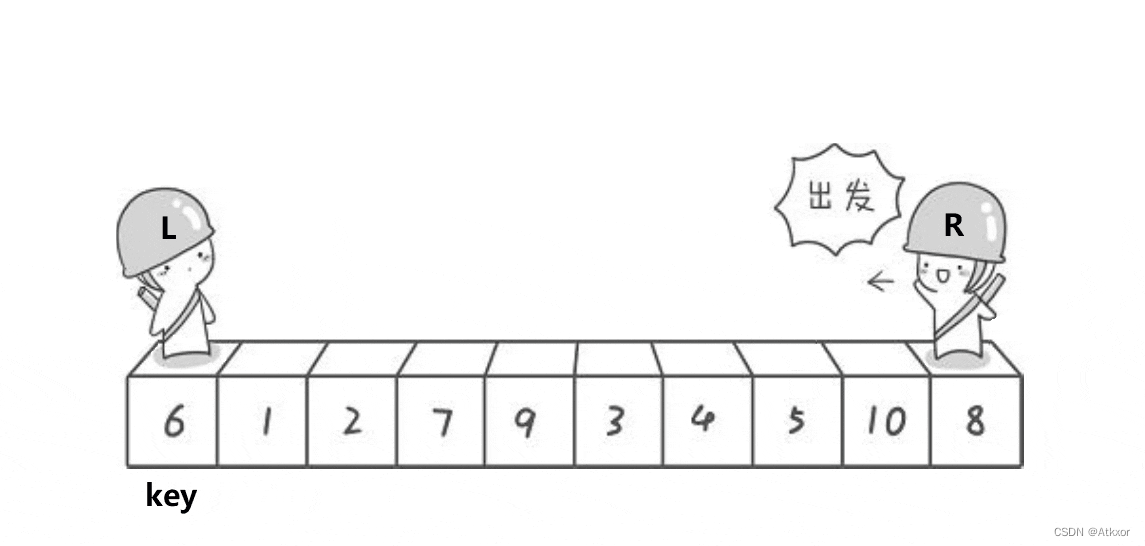
特点:采用分治算法
时间复杂度:
最好情况:O(nlong(n)) (区间分割,组成形式可以考虑为二叉树形式,最好情况就成了单支树,分治算法变成了减治算法)
平均情况:O(nlong(n))
最差情况:O(n2)
空间复杂度:O(log(n))—O(n)
稳定性:不稳定
选择排序
简单选择排序
每一次从待排序的元素中选出最小的一个元素,若它不是这组元无序素中的最后一个元素,则将它与存放这组有序元素的起始位置交换,直到全部待排序元素全部排完。
或是从无序元素中选出一个最大的,若其不是无序区间的最后一个元素,则将其与存放有序区间的最后一个元素交换,直到无序元素全部排完
特点:效率不高,算法的本质是减治算法
时间复杂度:
最好情况:O(n2)
平均情况:O(n2)
最坏情况:O(n2)
空间复杂度:O(1)
稳定性:不稳定
堆排序
利用堆的特点设计的一种排序算法,排升序要建大堆,排降序要建小堆,建堆是从第一个非叶子节点开始建,利用向下调整的思想逐步建立出整个堆
每次将未排序序列的第一个与最后一个元素进行交换,然后利用向下调整,将最大的元素调整到最后一个。
特点:算法的本质是减治算法
时间复杂度:
最好情况:O(nlongn)
平均情况:O(nlongn)
最坏情况:O(n*longn)
空间复杂度:O(1)
稳定性:不稳定
归并排序(稳定)
算法思想:把数组平均分成两部分,分别对左右两部分做均分,直到区间的size<=1,然后利用一个额外的数组空间,逐步将两个数组按序排列,再将排好的数据拷贝回原始数组,这样使子序列的段间有序,将子序列归并为完整的序列
特点:分治算法,是外部排序最好的算法
时间复杂度:
最好情况:O(n*log(n))
空间复杂度:O(n)
稳定性:稳定
基数排序(稳定)
算法思想:若分配的是数字,数字范围是0~9,所以需假设有10个桶来放关键字,每个桶分别代表0,1,2,3 、、、9,然后所有数字要位数相同,不够用0来补(如12,补为012),以三位数为例(原始序列中,位数最长的关键字是三位数),需要进行三次分配,第一次按个位分配,个位是几就放入几号桶,全部放完之后,从0号桶开始按顺序取出桶内的数,注意如果一个桶内放了多个关键字,则要按先进先出的原则取出桶内的关键字。第二次按十位分配,原理同上,第三次按百位分配,最后按原则取出关键字后即可得到一个有序序列。
(1)通过键值得各个位的值,将要排序的元素分配至一些桶中,达到排序的作用
(2)基数排序法是属于稳定性的排序,基数排序法是效率高的稳定排序法
(3)基数排序是桶排序的扩展
特
点:算法的本质是减治算法
时间复杂度:(r个队列,d趟分配)
最好情况:O(d(n+r))
平均情况:O(d(n+r))
最坏情况:O(d(n+r))
空间复杂度:O®
稳定性:稳定
多路归并排序(外排序)
二路归并排序是每次将数组分割为两个子数组,多路归并排序是将数组分割为多个子数组进行归并,其他方面和二路归并相同。可以将二路归并看作二叉树,多路为多叉树。
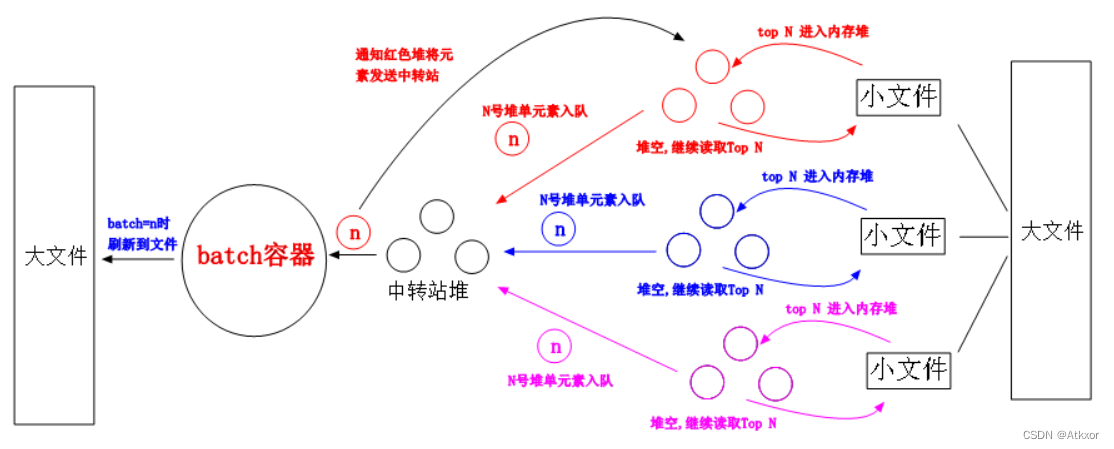
总结
知识点总结
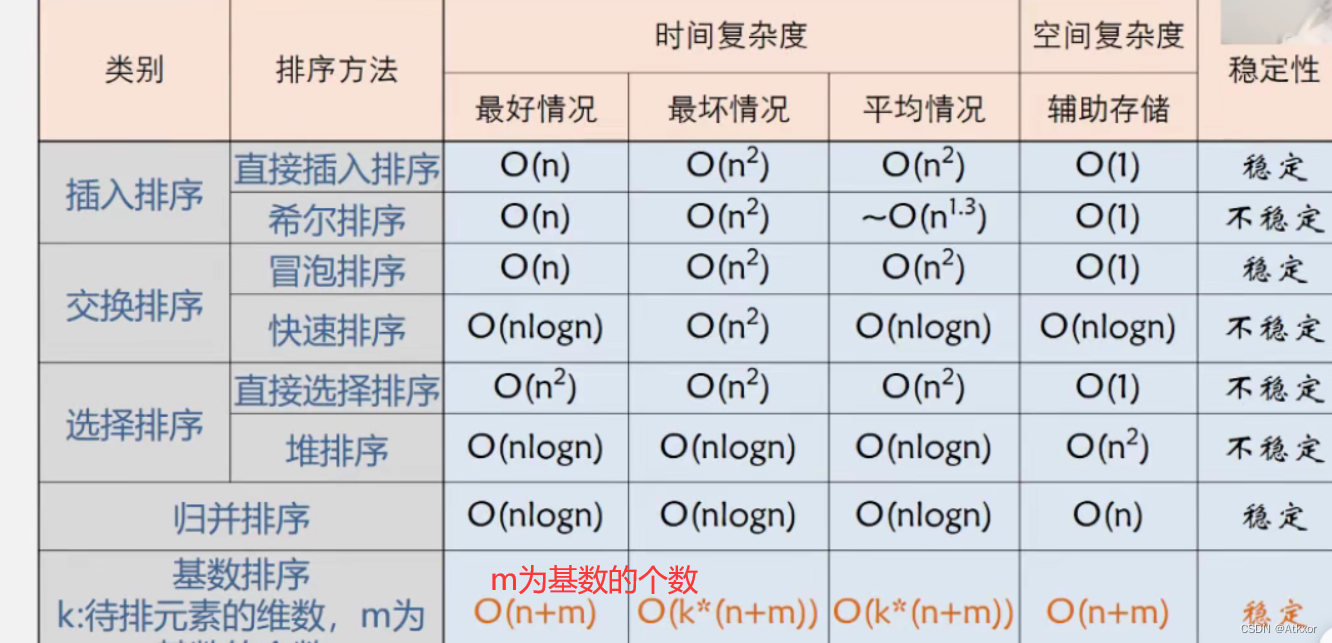
算法的稳定性
排序前后,相同关键字的次序(相对位置)若一致则稳定,不一致则不稳定。
稳定:冒泡排序、直接插入排序、归并排序、基数排序
不稳定:快速排序、希尔排序、堆排序、简单选择排序
比较次数 与 序列初态
无关:二路归并排序、简单选择排序、基数排序
有关:快速排序、直接插入排序、冒泡排序、堆排序、希尔排序
排序趟数 与 序列初态
无关:直接插入排序、折半插入排序、希尔排序、简单选择排序、归并排序、基数排序
有关 :冒泡排序、快速排序
比较次数 与 初始状态
无关:简单选择排序
有关 :插入排序、冒泡排序、快速排序
时间复杂度为O(nlog2n): 快排、归并、堆排
最好情况达到线性:冒泡(正向判断)、插入(逆向判断)
题目总结
1.判断稳定性

2.排序趟数与初始状态无关

3.移动次数与初始状态无关

4.比较次数与初始状态无关

5.每一趟排序结束都至少能够确定一个元素最终位置的方法

6.待排元素基本有序,效率最高的排序算法
7.就平均性能而言,目前最好.的内排序算法

快速排序 > 归并排序 > 希尔排序 > 堆排序
动态排序过程
六大排序算法





![[附源码]java毕业设计全国人口普查管理系统论文](https://img-blog.csdnimg.cn/8f9fa5ecde164b7d9af2fd0eeb7b801b.png)

![[附源码]java毕业设计汽车租赁系统](https://img-blog.csdnimg.cn/39f586b0e2f545dd881690c6cdbb847c.png)