今日主要总结一下动态规划的一道题目，746. 使用最小花费爬楼梯

题目：746. 使用最小花费爬楼梯

题目描述：
给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。

• 支付 15 ，向上爬两个台阶，到达楼梯顶部。
  总花费为 15 。
  示例 2：

输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。

• 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
• 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
• 支付 1 ，向上爬一个台阶，到达楼梯顶部。
  总花费为 6 。

提示：

2 <= cost.length <= 1000
0 <= cost[i] <= 999

本题重难点

大家在做这道题之前最好做一下70. 爬楼梯
这道题，本题是70. 爬楼梯的进阶版
或者看一下一文搞懂动态规划系列（第一篇）509. 斐波那契数70. 爬楼梯我对爬楼梯这道题有详细的讲解

对于动态规划问题，可以拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

后面的讲解中我都是围绕着这五点来进行讲解。

可能刷过动态规划题目的同学可能都知道递推公式的重要性，感觉确定了递推公式这道题目就解出来了。
其实 确定递推公式 仅仅是解题里的一步而已！
一些同学知道递推公式，但搞不清楚dp数组应该如何初始化，或者正确的遍历顺序，以至于记下来公式，但写的程序怎么改都通过不了。
后序的讲解的大家就会慢慢感受到这五步的重要性了。

1. 首先确定dp数组以及下标的含义
   使用动态规划，就要有一个数组来记录状态，本题只需要一个一维数组dp[i]就可以了。
   dp[i]的定义(往往就是题目要最终求得的结果)：本题即到达第i台阶所花费的最少体力为dp[i]。
   对于dp数组的定义，大家一定要清晰！

2. 第二步是确定递推公式
   一些同学可能想为什么要先确定递推公式，然后在考虑初始化呢？——因为一些情况是递推公式决定了dp数组要如何初始化！
   确定递推公式
   可以有两个途径得到dp[i]，一个是dp[i-1] 一个是dp[i-2]。
   dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
   dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
   那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢？
   一定是选最小的，所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);

3. dp数组如何初始化
   看一下递归公式，dp[i]由dp[i - 1]，dp[i - 2]推出，既然初始化所有的dp[i]是不可能的，那么只初始化dp[0]和dp[1]就够了，其他的最终都是dp[0]dp[1]推出。
   那么 dp[0] 应该是多少呢？ 根据dp数组的定义，到达第0台阶所花费的最小体力为dp[0]，那么有同学可能想，那dp[0] 应该是 cost[0]，例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话，dp[0] 就是 cost[0] 应该是1。
   题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 从 到达 第 0 个台阶是不花费的，但从 第0 个台阶 往上跳的话，需要花费 cost[0]。
   所以初始化 dp[0] = 0，dp[1] = 0;

4. 确定遍历顺序
   最后一步，递归公式有了，初始化有了，如何遍历呢？
   本题的遍历顺序其实比较简单，简单到很多同学都忽略了思考这一步直接就把代码写出来了。
   因为是模拟台阶，而且dp[i]由dp[i-1]dp[i-2]推出，所以是从前到后遍历cost数组就可以了。
   但是稍稍有点难度的动态规划，其遍历顺序并不容易确定下来。 例如：01背包，都知道两个for循环，一个for遍历物品嵌套一个for遍历背包容量，那么为什么不是一个for遍历背包容量嵌套一个for遍历物品呢？ 以及在使用一维dp数组的时候遍历背包容量为什么要倒序呢？这个系列会持续更新，后面会讲到！

5. 举例推导dp数组
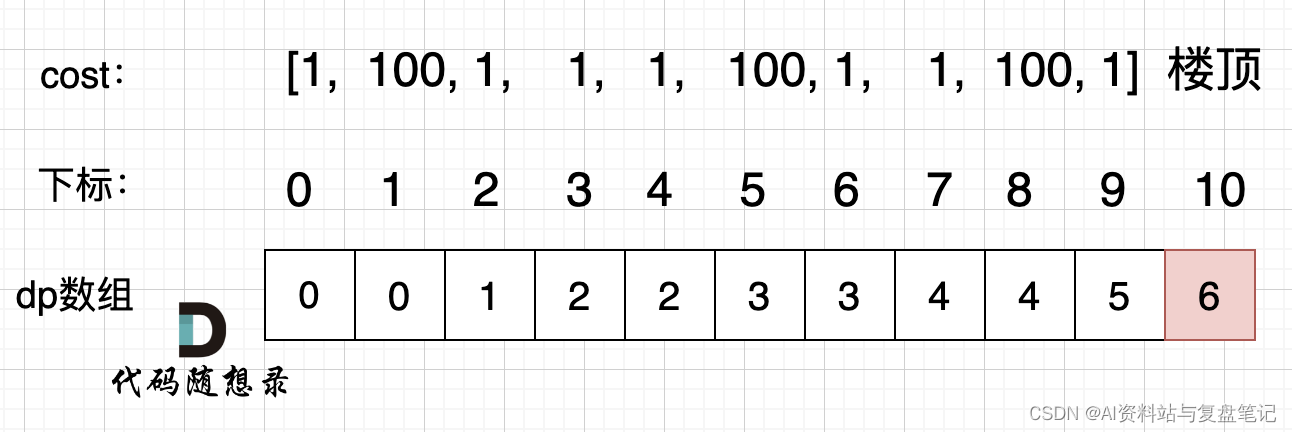
   拿示例2：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ，来模拟一下dp数组的状态变化，如下：

如果大家代码写出来有问题，就把dp数组打印出来，看看和如上推导的是不是一样的。

C++代码

方法一、常规动态规划

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        vector<int> dp(cost.size() + 1);
        dp[0] = 0; // 默认第一步都是不花费体力的
        dp[1] = 0;
        for (int i = 2; i <= cost.size(); i++) {
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.size()];
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

方法二、动归空间复杂度优化

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int dp0 = 0;
        int dp1 = 0;
        int res;
        for(int i = 2; i <= cost.size(); i++){
            res = min((dp0 + cost[i - 2]), (dp1 + cost[i - 1]));
            dp0 = dp1;
            dp1 = res;
        }
        return res;
    }
};

时间复杂度：O(n)
空间复杂度：O(1)

这一题比较简单主要是题目描述就已经把动规五部曲里的递归公式和如何初始化都给出来了，剩下几部曲也自然而然的推出来了，但是还是要清楚地理解每一步，因为一般题目都是要寄几分析推导递推公式和如何初始化！

---

总结

动态规划
英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。
动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的

对于动态规划问题，可以拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

后面的讲解中我都是围绕着这五点来进行讲解。

可能刷过动态规划题目的同学可能都知道递推公式的重要性，感觉确定了递推公式这道题目就解出来了。
其实 确定递推公式 仅仅是解题里的一步而已！
一些同学知道递推公式，但搞不清楚dp数组应该如何初始化，或者正确的遍历顺序，以至于记下来公式，但写的程序怎么改都通过不了。
后序的讲解的大家就会慢慢感受到这五步的重要性了。

---

欢迎大家关注本人公众号：编程复盘与思考随笔

(关注后可以免费获得本人在csdn发布的资源源码)