一、前言

又是一个复习的算法题目，下面直接看题吧。

二、题一：二叉树的最近公共祖先

1、上链接

236. 二叉树的最近公共祖先 - 力扣（Leetcode）

2、基本思路

有两种方法可解。

（1）朴素法

假设给定两个节点p，q，那么我们应该找出两条路径并存起来，路径是从根节点到给定节点，怎么找呢？利用栈进行递归查找即可。

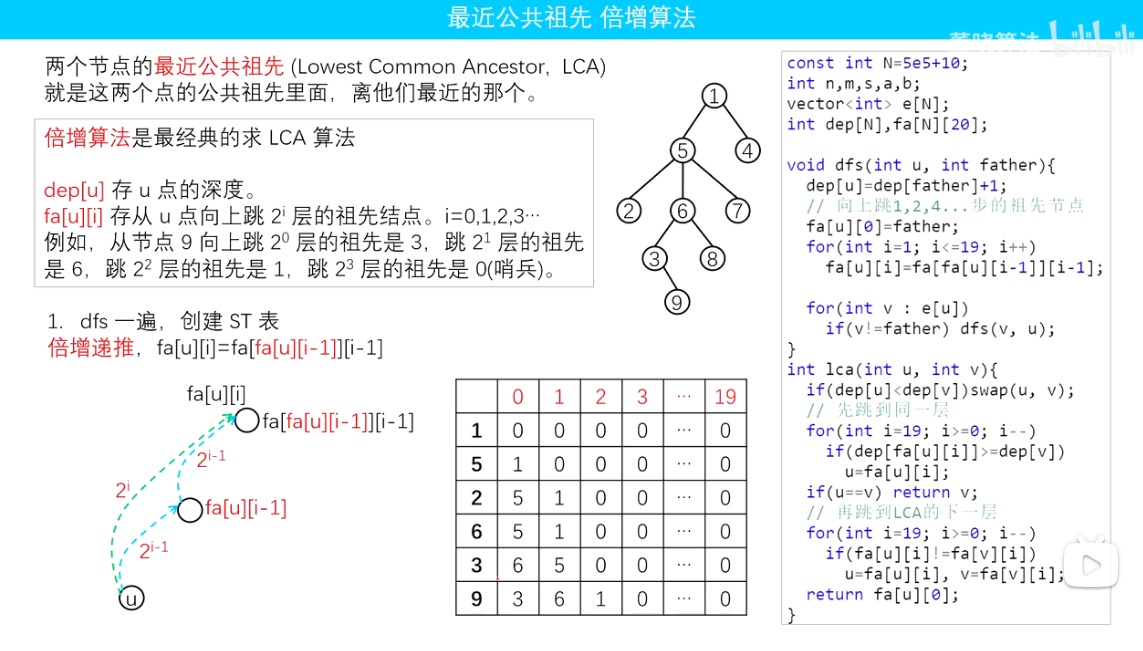
（2）LCA倍增法。

为什么倍增法可行，因为一个整型数永远可以化成一个二进制数（二进制转十进制）。

3、朴素法代码

（1）C++（AC）

顺便也复习了一下怎么建树。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;

///**
// * Definition for a binary tree node.
// */
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
	int* nums;
public:
	Solution(){
		nums=new int[11];
		int n[]={3,5,1,6,2,0,8,-1,-1,7,4};
		for(int i=0;i<11;++i)
			nums[i]=n[i];

//		for(int i=0;i<11;++i)
//			cout<<nums[i]<<" ";
//		cout<<endl;
	}

	void display(TreeNode* node){
		if(node){
			display(node->left);
			cout<<node->val<<endl;
			display(node->right);
		}
	}

	TreeNode* createTree(int idx){
		if(idx>10)
			return NULL;
		//cout<<idx<<endl;
		int num=nums[idx];
		TreeNode* t;
		if(num==-1){
			t = NULL;
		}else{
			t=new TreeNode(num);
			t->left=createTree(2*idx+1);
			t->right=createTree(2*idx+2);
		}
		return t;
	}

	void dfs_search(TreeNode* node,TreeNode* target,vector<TreeNode *> &stack,vector<TreeNode*> &path){
		if(node==NULL)
			return;
		stack.push_back(node);
//        cout<<node->val<<endl;
		if(node->val==target->val){
//			path=stack;
			path.assign(stack.begin(),stack.end());
			return;
		}
//        cout<<"2"<<endl;
		dfs_search(node->left,target,stack,path);
		dfs_search(node->right,target,stack,path);
		stack.pop_back();
	}

	//朴素法  用时击败16.68%，内存击败7.59%
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode *> p_path;
        vector<TreeNode *> q_path;
        vector<TreeNode *> stack;

        dfs_search(root,p,stack,p_path);
        stack.clear();
        dfs_search(root,q,stack,q_path);
//
//        for(int i=0;i<p_path.size();++i)
//            cout<<p_path[i]->val<<" ";
//        cout<<endl;
//        for(int i=0;i<q_path.size();++i)
//            cout<<q_path[i]->val<<" ";
//        cout<<endl;

        TreeNode* common;
        int i=0;
        while(i<p_path.size() && i<q_path.size()){
        	if(p_path[i]==q_path[i]){
        		common=p_path[i];
			}
			i++;
		}
		return common;
    }
};

int main(){
	Solution Tree;
	TreeNode* root=Tree.createTree(0);
//	Tree.display(root);
	int p,q;
	cin>>p>>q;
	TreeNode* pp=new TreeNode(p);
	TreeNode* qq=new TreeNode(q);

	TreeNode* ans=Tree.lowestCommonAncestor(root,pp,qq);
	cout<<ans->val<<endl;

	return 0;
}

（2）python（29/31，时间超限了但算法正确性是可以保证的）

import copy

class TreeNode():   # python 没有结构体，但可以用类实现相同效果
    def __init__(self,val:int,left=None,right=None):
        self.val=val
        self.left=left
        self.right=right

def Create_Tree(node,vals,idx):
    if idx>10:
        return node
    if vals[idx]=='#':
        node=None
    else:
        node=TreeNode(int(vals[idx]))
        node.left=Create_Tree(node.left,vals,2*idx+1)  
        node.right=Create_Tree(node.right,vals,2*idx+2)
    return node

def display(root):
    if root:
        display(root.left)
        print(root.val)
        display(root.right)

class Solution:
    def __init__(self):
        self.p_path=[]
        self.q_path=[]
        self.stack=[]

    def dfs_search(self,node:'TreeNode',target:'TreeNode',flg):
        if node==None:
            return
        self.stack.append(node)
        if node.val == target.val:
            if flg==0:
                self.p_path=copy.deepcopy(self.stack)
            else:
                self.q_path=copy.deepcopy(self.stack)
            return
        self.dfs_search(node.left,target,flg)
        self.dfs_search(node.right,target,flg)
        self.stack.pop()
    
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        self.dfs_search(root,p,0)
        self.stack.clear()
        self.dfs_search(root,q,1)

        common=TreeNode(None);
        i=0
        while i<len(self.p_path) and i<len(self.q_path):
            if self.p_path[i].val==self.q_path[i].val:
                common=copy.deepcopy(self.p_path[i])
            i+=1
        return common

   
if __name__=='__main__':
    node=None
    vals=list("3516208##74")
    root=Create_Tree(node,vals,0)
##    display(root)
    n1,n2=map(int,input().split())
    p=TreeNode(n1)
    q=TreeNode(n2)

    sol=Solution()
    ans=sol.lowestCommonAncestor(root,p,q)
    print(ans.val)

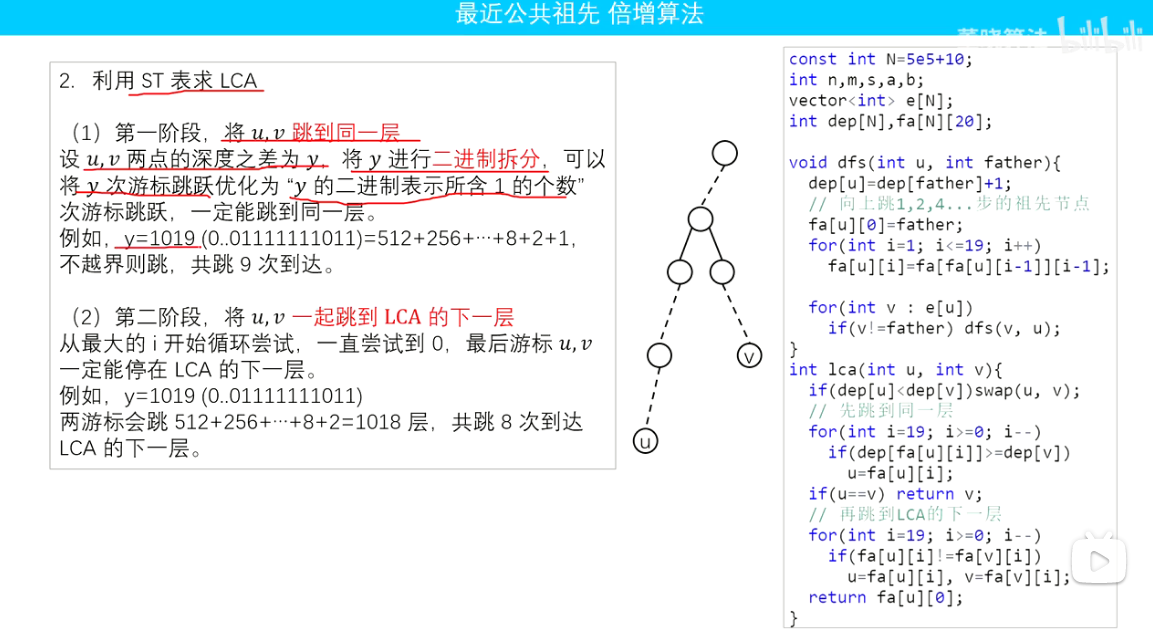
4、LCA倍增法

（1）C++（不提交，因为不想补全力扣给的入口函数，但是能保证算法正确性）

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;

const int N=10010;
int n,m,cnt=1;
struct Edge{
	int to,w,next;
}edge[N];
int head[N],dep[N],fa[N][N];

void Add(int u,int v){
	edge[cnt].to=v;
	edge[cnt].next=head[u];
//	edge[cnt].w=w;
	head[u]=cnt;
//	cout<<"对于"<<u<<" "<<v<<"这条边"<<cnt<<" "<<edge[cnt].next<<" "<<edge[cnt].to<<" "<<head[u]<<endl;
	cnt++;
}

//int k=0; 
void dfs(int v,int father){  //填深度表和跳步表 
	dep[v]=dep[father]+1;
	fa[v][0]=father;
	for(int i=1;i<=19;++i)
		fa[v][i]=fa[fa[v][i-1]][i-1];
	
	for(int i=head[v];i;i=edge[i].next){
		int p=edge[i].to;
//		cout<<k<<" "<<i<<" "<<p<<endl;
//		k++;
		if(p!=father)
			dfs(p,v);	
	}
}

int lca(int x,int y){
//	cout<<dep[0]<<" "<<dep[x]<<" "<<dep[y]<<endl;
	if(dep[x]<dep[y])
		swap(x,y);
	for(int i=19;i>=0;i--)   //先跳到同一层 
		if(dep[fa[x][i]]>=dep[y]){
			x=fa[x][i];
//			cout<<"* "<<fa[x][i]<<endl;
		}
			
//	cout<<"11"<<endl;
	if(x==y)
		return y;
//	cout<<"22"<<endl;
	for(int i=19;i>=0;i--){  //再跳到lca的下一层 
		if(fa[x][i]!=fa[y][i]){
			x=fa[x][i],y=fa[y][i];
		}		
	}
	return fa[x][0];
}


struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Tree{
public:
	int nums[11] = {3,5,1,6,2,9,8,-1,-1,7,4};  //因为样例中有一个节点的值为0，导致dep[0]被更改了，所以调试了很久，这个样例我把0换成了9 
//	int nums[2]={1,2};
	TreeNode* createTree(int idx){
		if(idx>10)
			return NULL;
		TreeNode* t;
		if(nums[idx]==-1){
			t=NULL;
			return t;
		}else{
			t=new TreeNode(nums[idx]);
			t->left= createTree(2*idx+1);
			t->right=createTree(2*idx+2);
		}
		return t;
	}
	void display(TreeNode* node){
		if(node){
			display(node->left);
			cout<<node->val<<endl;
			display(node->right);
		}
	}
	void add_edge(TreeNode* node){ //链式前向星加边，当然也可以根据数组下标加边，这里建树再加边的操作略显复杂 
		if(node->left!=NULL){
			Add(node->val,node->left->val);
			Add(node->left->val,node->val);
			add_edge(node->left);
		}
		if(node->right!=NULL){
			Add(node->val,node->right->val);
			Add(node->right->val,node->val);
			add_edge(node->right);
		}	
	}		
};


int main(){
	Tree* t=new Tree();
	TreeNode* root=t->createTree(0);
//	t->display(root);
	t->add_edge(root);
//	cout<<root->val<<endl;
//	cout<<"dep[0]: "<<dep[0]<<endl;
	dfs(root->val,0);
	int x,y;
	cin>>x>>y;
	int ans=lca(x,y);
	cout<<ans<<endl;
	
	return 0;
}

5、其他递归法

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == NULL)
            return NULL;
        if(root == p || root == q) 
            return root;
            
        TreeNode* left =  lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
       
        if(left == NULL)
            return right;
        if(right == NULL)
            return left;      
        if(left && right) // p和q在两侧
            return root;
        
        return NULL; // 必须有返回值
    }
};

三、题二：【模板】最近公共祖先（LCA）

1、上链接

P3379 【模板】最近公共祖先（LCA） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

2、基本思路

为倍增法量身定做的一道题，下面用链式前向星+倍增法搞定。

3、倍增法代码

（1）C++ （AC）

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;

int n,m,s; //树的结点个数、询问次数、树根节点的序号 
int x,y; //x和y之间有一条直接连接的边 
int a,b; //表示询问a和b的最近公共祖先 

const int N=5000100;
int cnt=1,head[N];
struct Edge{
	int to,next;
} e[N];

int dep[N],fa[N][22];

void Add(int x,int y){
	e[cnt].to=y;
	e[cnt].next=head[x];
	head[x]=cnt++;
}

void dfs(int u,int father){  //填深度表和跳步表 
	dep[u]=dep[father]+1; 
	fa[u][0]=father;
	for(int i=1;i<=19;++i)
		fa[u][i]=fa[fa[u][i-1]][i-1];
	
	for(int i=head[u];i;i=e[i].next){
		int p=e[i].to;
		if(p!=father)
			dfs(p,u);
	}
}

int lca(int x,int y){
	if(dep[x]<dep[y])
		swap(x,y);
	for(int i=19;i>=0;i--)    //跳到同一层 
		if(dep[fa[x][i]]>=dep[y])
			x=fa[x][i];
			
	if(x==y)
		return y;
	
	for(int i=19;i>=0;i--)
		if(fa[x][i]!=fa[y][i])
			x=fa[x][i],y=fa[y][i];
	
	return fa[x][0];
	
}

int main(){
	cin>>n>>m>>s;
	for(int i=0;i<n-1;++i){
		cin>>x>>y;
		Add(x,y);
		Add(y,x);
	} 
	dfs(s,0);
//	cout<<lca(4,5)<<endl; 
	for(int i=0;i<m;i++){
		cin>>a>>b;
		cout<<lca(a,b)<<endl; 
	}
	return 0;
}

（2）python（70分）

N=500010
# 没办法，N=5000010会全部时间超限
cnt=1
head=[0]*N
next=[0]*N
to=[0]*N

dep=[0]*N
fa=[[0]*20 for _ in range(N)]

def Add(a,b):
    global cnt
    to[cnt]=b
    next[cnt]=head[a]
    head[a]=cnt
    cnt+=1

def dfs(u:int,father:int):   # 填深度表和跳步表
    dep[u]=dep[father]+1
    fa[u][0]=father
    for i in range(1,20):
        fa[u][i]=fa[fa[u][i-1]][i-1]

    i=head[u]
    while i:
        p=to[i]
        if p!=father:
            dfs(p,u)
        i=next[i]
    
def lca(x,y)->int:
    if dep[x]<dep[y]:
        x,y=y,x
    for i in range(19,-1,-1):    # 先跳到同一层
        if dep[fa[x][i]]>=dep[y]:
            x=fa[x][i]
    if x==y:
        return y
    for i in range(19,-1,-1):
        if fa[x][i]!=fa[y][i]:
            x,y=fa[x][i],fa[y][i]
    return fa[x][0]

n,m,s=map(int,input().split())
for i in range(n-1):
    x,y=map(int,input().split())
    Add(x,y)
    Add(y,x)
dfs(s,0)
for i in range(m):
    a,b=map(int,input().split())
    print(lca(a,b))

以上，最近公共祖先

祝好