1.2 极限的性质【极限】
1.2.1 唯一性
极限的唯一性
引入
-
假设警察逮捕罪犯,把犯人追到了悬崖边上,那么犯人只能在悬崖边束手就擒,这个时候悬崖边是犯人逃跑的极限位置,别无去处,位置唯一。

-
考试或比赛的时候都努力争取第一名,第一名是能够取得的最好的名次,第一名的名次是唯一的,不可能有另外的名次比第一名的成绩更靠前,也不可能两个不同的成绩都被评为第一名。

- 绝对零度
(英文:The Absolute Zero),是热力学的最低温度,热力学温标的单位是K(开尔文),绝对零度就是0K(约为-273.15℃或-459.67℉),绝对零度在现实中是无法达到的,只是理论的下限值,在此温度下,物体分子没有动能,在一个特定的物理状态下不可能同时存在两个不同的温度,即温度降低的极限值是唯一的。

唯一性
性质:如果数列或函数极限存在,那么极限唯一。
证明
反证法(数列与函数同理,以数列为例证明)
假设 { a n } \left\{a_{n}\right\} {an} 是一个收敛数列,并且有两个极限 K K K和 L \mathrm{L} L ,那么根据极限的定义:
对任意 ε > 0 \varepsilon>0 ε>0 , 存在 N 1 ∈ N , N 2 ∈ N N_{1} \in \mathbb{N}, N_{2} \in \mathbb{N} N1∈N,N2∈N , 使得 n > N 1 ⟹ ∣ a n − K ∣ < ε 2 , n > N 2 ⟹ ∣ a n − L ∣ < ε 2 n>N_{1} \Longrightarrow\left|a_{n}-K\right|<\frac{\varepsilon}{2}, n>N_{2} \Longrightarrow \mid a_{n} -L \mid<\frac{\varepsilon}{2} n>N1⟹∣an−K∣<2ε,n>N2⟹∣an−L∣<2ε
现在取 N = max { N 1 , N 2 } N=\max \left\{N_{1}, N_{2}\right\} N=max{N1,N2} , 则 n > N ⟹ ∣ a n − K ∣ < ϵ 2 n>N \Longrightarrow\left|a_{n}-K\right|<\frac{\epsilon}{2} n>N⟹∣an−K∣<2ϵ 并且 ∣ a n − L ∣ < ϵ 2 \left|a_{n}-L\right|<\frac{\epsilon}{2} ∣an−L∣<2ϵ
根据三角不等式, ∣ K − L ∣ ≤ ∣ K − a n ∣ + ∣ a n − L ∣ < ε 2 + ε 2 = ε |K-L| \leq\left|K-a_{n}\right|+\left|a_{n}-L\right|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon ∣K−L∣≤∣K−an∣+∣an−L∣<2ε+2ε=ε
上式对于所有的 ε > 0 \varepsilon>0 ε>0 都成立, 故 ∣ K − L ∣ = 0 , K = L |K-L|=0, K=L ∣K−L∣=0,K=L
1.2.2 有界性
引入
假如一个人蹦极:

设地面的高度是
0
0
0,跳台的高度是
H
H
H,下落的时间变量是
t
t
t,从跳台到最低点的实际时间是
T
T
T,从跳台上下落的距离是
s
(
t
)
s(t)
s(t),显然
s
(
t
)
s(t)
s(t)的值不会超过跳台的高度
H
H
H,否则就撞地上了,
s
(
t
)
s(t)
s(t)的取值范围是
[
0
,
H
)
[0,H)
[0,H),这个取值范围
[
0
,
H
)
[0,H)
[0,H)是可能的最大范围。实际运动到最低点下落的距离假设是
h
h
h,即
lim
t
→
T
s
(
t
)
=
h
<
H
\displaystyle\lim_{t \rightarrow T}s(t)=h<H
t→Tlims(t)=h<H
这里的
H
H
H就是极限取值的上界。
有界性
极限的有界性
(数列) 如果数列 { x n } \left\{x_{n}\right\} {xn}收敛, 那么数列 { x n } \left\{x_{n}\right\} {xn}一定有界。
例如:数列 x n = n + 1 n x_{n}=\frac{n+1}{n} xn=nn+1,数列极限为 1 1 1, x n x_{n} xn的上界是 2 2 2,下界是 1 1 1。
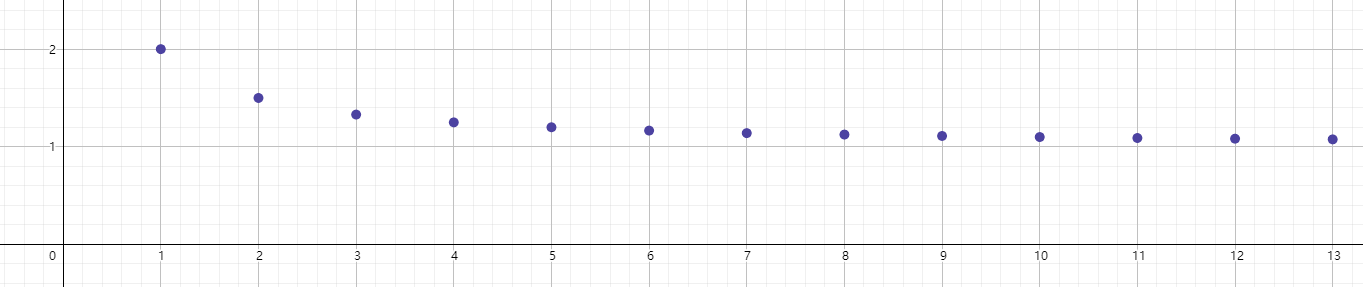
注意 反之不成立, 反例为 x n = ( − 1 ) n x_{n}=(-1)^{n} xn=(−1)n。显然,该数列有界但不收敛,由此可得有界是数列收敛的必要条件而非充分条件,无界数列一定发散,但发散数列不一定无界。
(函数) 若 lim x → x 0 f ( x ) \displaystyle\lim _{x \rightarrow x_{0}} f(x) x→x0limf(x) 存在, 则 f ( x ) f(x) f(x)在 x 0 x_{0} x0 某去心邻域有界 (即局部有界)。
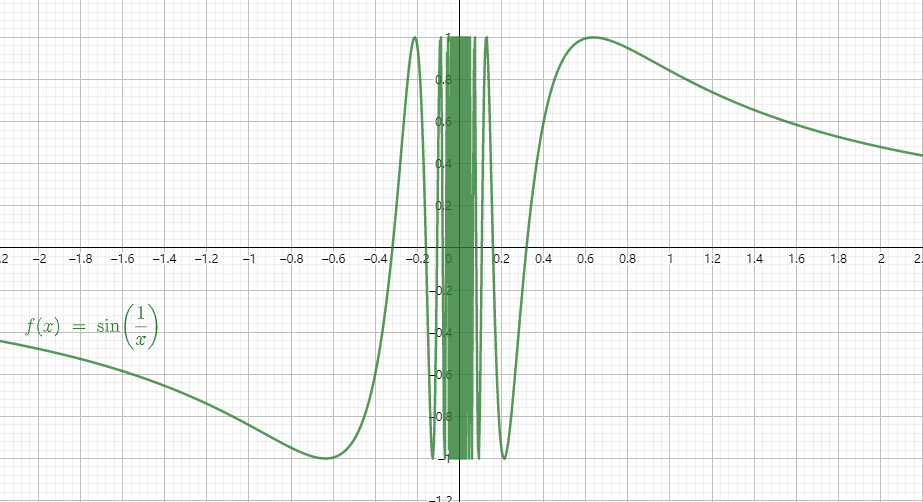
注意 反之不成立, 反例为 f ( x ) = sin 1 x f(x)=\sin \frac{1}{x} f(x)=sinx1,该函数在 x = 0 x=0 x=0的去心邻域有界,但它在 x = 0 x= 0 x=0处的极限 lim x → 0 sin 1 x \displaystyle\lim _{x \rightarrow 0} \sin \frac{1}{x} x→0limsinx1不存在.
综上:收敛必有界,有界未必收敛。
1.2.3 保号性
引入
通俗的讲,保号性就是数列项数 n n n趋于无穷的过程中,或函数自变量在接近某一点时,数列项或函数值的正负号会变得和极限值的正负号一样。
定义
(数列) 设 lim x n = A \lim x_{n}=A limxn=A.
-
如果 A > 0 A>0 A>0 (或 A < 0 A<0 A<0 ), 则存在 N > 0 N>0 N>0, 当 n > N n>N n>N 时, x n > 0 x_{n}>0 xn>0(或 x n < 0 x_{n}<0 xn<0) ;
-
如果存在 N > 0 N>0 N>0, 当 n > N n>N n>N 时, x n ⩾ 0 x_{n} \geqslant 0 xn⩾0(或 x n ⩽ 0 x_{n} \leqslant 0 xn⩽0 ), 则 A ⩾ 0 A \geqslant 0 A⩾0 (或 A ⩽ 0 A \leqslant 0 A⩽0 ).
(函数) 设 lim x → x 0 f ( x ) = A \displaystyle\lim _{x \rightarrow x_{0}} f(x)=A x→x0limf(x)=A.
-
如果 A > 0 A>0 A>0 (或 A < 0 A<0 A<0 ), 则存在 δ > 0 \delta>0 δ>0, 当 x ∈ U ˚ ( x 0 , δ ) x \in \mathring{U}\left(x_{0}, \delta\right) x∈U˚(x0,δ) 时, f ( x ) > 0 f(x)>0 f(x)>0( 或 f ( x ) < 0 f(x)<0 f(x)<0) .
-
如果存在 δ > 0 \delta>0 δ>0, 当 x ∈ U ∘ ( x 0 , δ ) x \in \stackrel{\circ}{U}\left(x_{0}, \delta\right) x∈U∘(x0,δ)时, f ( x ) ⩾ 0 f(x) \geqslant 0 f(x)⩾0 (或 f ( x ) ⩽ 0 f(x) \leqslant 0 f(x)⩽0 ), 那么 A ⩾ 0 A \geqslant 0 A⩾0 (或 A ⩽ 0 A \leqslant 0 A⩽0 ).
如果取 f ( x ) > 0 f(x) > 0 f(x)>0 (或 f ( x ) < 0 f(x) < 0 f(x)<0 ), 那么 A ⩾ 0 A \geqslant 0 A⩾0 (或 A ⩽ 0 A \leqslant 0 A⩽0 )此处依然取等。
注意
上述结论 1. 中是严格不等号 ( > > > 或 < < <,不包含 = = =) 。
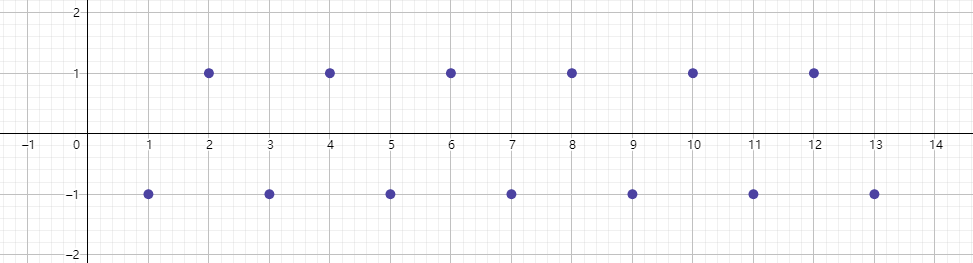
如下图所示 f ( x ) = s i n ( x ) x f(x)=\frac{sin(x)}{x} f(x)=xsin(x),数列 x n = s i n ( n ) n x_n=\frac{sin(n)}{n} xn=nsin(n)是此函数上的点, lim x → ∞ x n = s i n ( n ) n = 0 \displaystyle\lim _{x\rightarrow \infty}x_n=\frac{sin(n)}{n}=0 x→∞limxn=nsin(n)=0, x n x_n xn在会在正负之间不断变化,不会在某一个 N N N之后 x n x_n xn大于 0 0 0或小于 0 0 0。

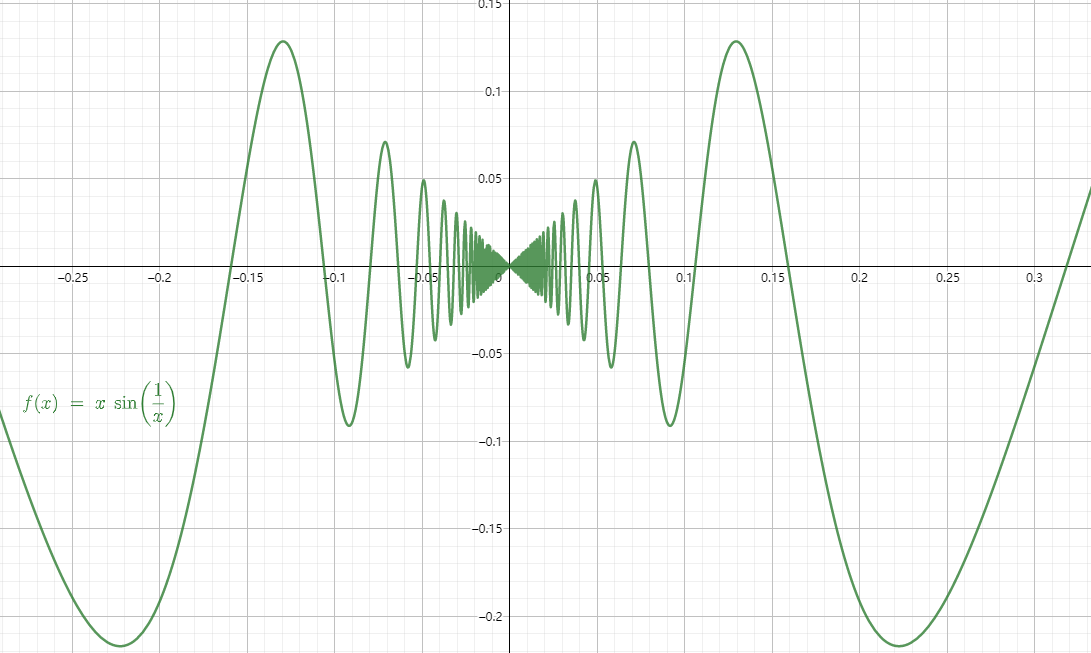
如下如所示, lim x → x 0 f ( x ) = lim x → x 0 x s i n 1 x = 0 \displaystyle\lim _{x\rightarrow x_{0}}f(x)=\displaystyle\lim _{x\rightarrow x_{0}}xsin\frac{1}{x}=0 x→x0limf(x)=x→x0limxsinx1=0, x ∈ U ∘ ( 0 , δ ) x \in \stackrel{\circ}{U}\left(0, \delta\right) x∈U∘(0,δ)函数值不具有保号性。
上述结论 2. 中是非严格不等号 ( ⩾ \geqslant ⩾ 或 ⩽ \leqslant ⩽) ,不论数列项或函数值是否取到 0 0 0,极限值都可以取到 0 0 0。
如果结论 2. 中取 x n > 0 x_{n} > 0 xn>0(或 x n < 0 x_{n} < 0 xn<0 ), f ( x ) > 0 f(x) > 0 f(x)>0 (或 f ( x ) < 0 f(x) < 0 f(x)<0 ),则 A ⩾ 0 A \geqslant 0 A⩾0 (或 A ⩽ 0 A \leqslant 0 A⩽0 ),极限依然取等号。
考研真题
极限保号性的应用
(1995, 数三) 设
lim
x
→
a
f
(
x
)
−
f
(
a
)
(
x
−
a
)
2
=
−
1
\displaystyle\lim _{x \rightarrow a} \frac{f(x)-f(a)}{(x-a)^{2}}=-1
x→alim(x−a)2f(x)−f(a)=−1 , 则在点
x
=
a
x=a
x=a 处
(A)
f
(
x
)
f(x)
f(x) 的导数存在, 且
f
′
(
a
)
≠
0
f^{\prime}(a) \neq 0
f′(a)=0 .
(B)
f
(
x
)
f(x)
f(x) 取得极大值.
(C)
f
(
x
)
f(x)
f(x) 取得极小值.
(D)
f
(
x
)
f(x)
f(x) 的导数不存在.
【解 1】极限保号性的应用
因为
lim
x
→
a
f
(
x
)
−
f
(
a
)
(
x
−
a
)
2
=
−
1
<
0
\displaystyle\lim _{x \rightarrow a} \frac{f(x)-f(a)}{(x-a)^{2}}=-1<0
x→alim(x−a)2f(x)−f(a)=−1<0 ,由极限保号性知,存在
δ
>
0
\delta>0
δ>0 , 当
x
∈
U
∘
(
a
,
δ
)
x \in \stackrel{\circ}{U}(a, \delta)
x∈U∘(a,δ) 时,
f
(
x
)
−
f
(
a
)
(
x
−
a
)
2
<
0
\frac{f(x)-f(a)}{(x-a)^{2}}<0
(x−a)2f(x)−f(a)<0
又因为当
x
∈
U
∘
(
a
,
δ
)
x \in \stackrel{\circ}{U}(a, \delta)
x∈U∘(a,δ) 时,
(
x
−
a
)
2
>
0
(x-a)^{2}>0
(x−a)2>0 , 则
f
(
x
)
−
f
(
a
)
<
0
f(x)-f(a)<0
f(x)−f(a)<0 , 即
f
(
x
)
<
f
(
a
)
f(x)<f(a)
f(x)<f(a),由极值的定义得在点
x
=
a
x=a
x=a 处
f
(
x
)
f(x)
f(x) 取得极大值.
【解 2】取特值法
令 f ( x ) = − ( x − a ) 2 f(x)=-(x-a)^{2} f(x)=−(x−a)2 , 显然 f ( x ) f(x) f(x) 满足题设条件, 但在 x = a x=a x=a 处 f ( x ) f(x) f(x) 可导且 f ′ ( a ) = 0 f^{\prime}(a)=0 f′(a)=0 , 取极大值, 则选项 (A) © (D) 都不正确, 故应选 (B).