2460. 对数组执行操作

给你一个下标从 0 开始的数组 nums ，数组大小为 n ，且由 非负 整数组成。

你需要对数组执行 n - 1 步操作，其中第 i 步操作（从 0 开始计数）要求对 nums 中第 i 个元素执行下述指令：

• 如果 nums[i] == nums[i + 1] ，则 nums[i] 的值变成原来的 2 倍，nums[i + 1] 的值变成 0 。否则，跳过这步操作。

在执行完 全部 操作后，将所有 0 移动 到数组的 末尾 。

• 例如，数组 [1,0,2,0,0,1] 将所有 0 移动到末尾后变为 [1,2,1,0,0,0] 。

返回结果数组。

注意 操作应当 依次有序 执行，而不是一次性全部执行。

提示：

• 2 <= nums.length <= 2000
• 0 <= nums[i] <= 1000

示例

输入：nums = [1,2,2,1,1,0]
输出：[1,4,2,0,0,0]
解释：执行以下操作：
- i = 0: nums[0] 和 nums[1] 不相等，跳过这步操作。
- i = 1: nums[1] 和 nums[2] 相等，nums[1] 的值变成原来的 2 倍，nums[2] 的值变成 0 。数组变成 [1,4,0,1,1,0] 。
- i = 2: nums[2] 和 nums[3] 不相等，所以跳过这步操作。
- i = 3: nums[3] 和 nums[4] 相等，nums[3] 的值变成原来的 2 倍，nums[4] 的值变成 0 。数组变成 [1,4,0,2,0,0] 。
- i = 4: nums[4] 和 nums[5] 相等，nums[4] 的值变成原来的 2 倍，nums[5] 的值变成 0 。数组变成 [1,4,0,2,0,0] 。
执行完所有操作后，将 0 全部移动到数组末尾，得到结果数组 [1,4,2,0,0,0] 。

思路

简单模拟题，使用双指针，可以进行原地删除。

// C++
class Solution {
public:
    vector<int> applyOperations(vector<int>& nums) {
        int n = nums.size(), i = 0, j = 0;
        while (i < n) {
            if (nums[i] != 0) {
                if (i + 1 < n && nums[i] == nums[i + 1]) nums[j++] = 2 * nums[i++];
                else nums[j++] = nums[i];
            }
            i++;
        }
        while (j < n) nums[j++] = 0;
        return nums;
    }
};

2461. 长度为 K 子数组中的最大和

给你一个整数数组 nums 和一个整数 k 。请你从 nums 中满足下述条件的全部子数组中找出最大子数组和：

• 子数组的长度是 k，且
• 子数组中的所有元素 各不相同 。

返回满足题面要求的最大子数组和。如果不存在子数组满足这些条件，返回 0 。

子数组 是数组中一段连续非空的元素序列。

提示：

• 1 <= k <= nums.length <= 105
• 1 <= nums[i] <= 105

示例

输入：nums = [1,5,4,2,9,9,9], k = 3
输出：15
解释：nums 中长度为 3 的子数组是：
- [1,5,4] 满足全部条件，和为 10 。
- [5,4,2] 满足全部条件，和为 11 。
- [4,2,9] 满足全部条件，和为 15 。
- [2,9,9] 不满足全部条件，因为元素 9 出现重复。
- [9,9,9] 不满足全部条件，因为元素 9 出现重复。
因为 15 是满足全部条件的所有子数组中的最大子数组和，所以返回 15 。

思路

简单滑动窗口，维护窗口内的和即可

// C++
typedef long long LL;
const int N = 1e5 + 10;
class Solution {
public:
    // 用于判重
    bool st[N];
    
    LL maximumSubarraySum(vector<int>& nums, int k) {
        LL ans = 0, sum = 0;
        int n = nums.size();
        for (int i = 0, j = 0; i < n; i++) {
            // 当出现重复时
            while (st[nums[i]]) {
                st[nums[j]] = false;
                sum -= nums[j];
                j++;
            }
            st[nums[i]] = true; // 纳入当前窗口
            sum += nums[i];
            
            // 刚好>k, 则减1
            if (i - j + 1 > k) {
                st[nums[j]] = false;
                sum -= nums[j];
                j++;
            }
            
            if (i - j + 1 == k) ans = max(ans, sum);
        }
        return ans;
    }
};

2462. 雇佣 K 位工人的总代价

给你一个下标从 0 开始的整数数组 costs ，其中 costs[i] 是雇佣第 i 位工人的代价。

同时给你两个整数 k 和 candidates 。我们想根据以下规则恰好雇佣 k 位工人：

• 总共进行 k 轮雇佣，且每一轮恰好雇佣一位工人。

• 在每一轮雇佣中，从最前面candidates和最后面candidates

  人中选出代价最小的一位工人，如果有多位代价相同且最小的工人，选择下标更小的一位工人。

  • 比方说，costs = [3,2,7,7,1,2] 且 candidates = 2 ，第一轮雇佣中，我们选择第 4 位工人，因为他的代价最小 [*3,2*,7,7,***1**,2*] 。
  • 第二轮雇佣，我们选择第 1 位工人，因为他们的代价与第 4 位工人一样都是最小代价，而且下标更小，[*3,**2***,7,*7,2*] 。注意每一轮雇佣后，剩余工人的下标可能会发生变化。

• 如果剩余员工数目不足 candidates 人，那么下一轮雇佣他们中代价最小的一人，如果有多位代价相同且最小的工人，选择下标更小的一位工人。

• 一位工人只能被选择一次。

返回雇佣恰好 k 位工人的总代价。

提示：

• 1 <= costs.length <= 10^5
• 1 <= costs[i] <= 10^5
• 1 <= k, candidates <= costs.length

示例

输入：costs = [17,12,10,2,7,2,11,20,8], k = 3, candidates = 4
输出：11
解释：我们总共雇佣 3 位工人。总代价一开始为 0 。
- 第一轮雇佣，我们从 [17,12,10,2,7,2,11,20,8] 中选择。最小代价是 2 ，有两位工人，我们选择下标更小的一位工人，即第 3 位工人。总代价是 0 + 2 = 2 。
- 第二轮雇佣，我们从 [17,12,10,7,2,11,20,8] 中选择。最小代价是 2 ，下标为 4 ，总代价是 2 + 2 = 4 。
- 第三轮雇佣，我们从 [17,12,10,7,11,20,8] 中选择，最小代价是 7 ，下标为 3 ，总代价是 4 + 7 = 11 。注意下标为 3 的工人同时在最前面和最后面 4 位工人中。
总雇佣代价是 11 。

思路

用一个小根堆，维护当前纳入考虑范围的所有candidates，并且维护左右两侧的边界。每次从堆顶弹出一个元素，累加这个元素的cost，并查看其下标，若其下标在[0, l]，则左侧边界往右拓展一位；反之若在右侧[r, n - 1]，则右侧边界往左拓展一位。

// C++
typedef long long LL;
typedef pair<int, int> PII;
class Solution {
public:
    LL totalCost(vector<int>& costs, int k, int c) {
        priority_queue<PII, vector<PII>, greater<PII>> heap;
        int n = costs.size(), l = c - 1, r = n - c;
        for (int i = 0; i <= l; i++) heap.push({costs[i], i});
        for (int i = n - 1; i >= r && i > l; i--) heap.push({costs[i], i});
        LL ans = 0;
        for (int i = 0; i < k; i++) {
            PII p = heap.top();
            heap.pop();
            ans += p.first;
            int pos = p.second;
            if (pos <= l && l + 1 < r) {
                heap.push({costs[l + 1], l + 1});
                l++;
            } else if (pos >= r && r - 1 > l) {
                heap.push({costs[r - 1], r - 1});
                r--;
            }
        }
        return ans;
    }
};

2463. 最小移动总距离

X 轴上有一些机器人和工厂。给你一个整数数组 robot ，其中 robot[i] 是第 i 个机器人的位置。再给你一个二维整数数组 factory ，其中 factory[j] = [position_j, limit_j] ，表示第 j 个工厂的位置在 position_j ，且第 j 个工厂最多可以修理 limit_j 个机器人。

每个机器人所在的位置 互不相同 。每个工厂所在的位置也 互不相同 。注意一个机器人可能一开始跟一个工厂在 相同的位置 。

所有机器人一开始都是坏的，他们会沿着设定的方向一直移动。设定的方向要么是 X 轴的正方向，要么是 X 轴的负方向。当一个机器人经过一个没达到上限的工厂时，这个工厂会维修这个机器人，且机器人停止移动。

任何时刻，你都可以设置 部分 机器人的移动方向。你的目标是最小化所有机器人总的移动距离。

请你返回所有机器人移动的最小总距离。测试数据保证所有机器人都可以被维修。

注意：

• 所有机器人移动速度相同。
• 如果两个机器人移动方向相同，它们永远不会碰撞。
• 如果两个机器人迎面相遇，它们也不会碰撞，它们彼此之间会擦肩而过。
• 如果一个机器人经过了一个已经达到上限的工厂，机器人会当作工厂不存在，继续移动。
• 机器人从位置 x 到位置 y 的移动距离为 |y - x| 。

提示：

• 1 <= robot.length, factory.length <= 100
• factory[j].length == 2
• -10^9 <= robot[i], position_j <= 10^9
• 0 <= limit_j <= robot.length
• 测试数据保证所有机器人都可以被维修。

示例

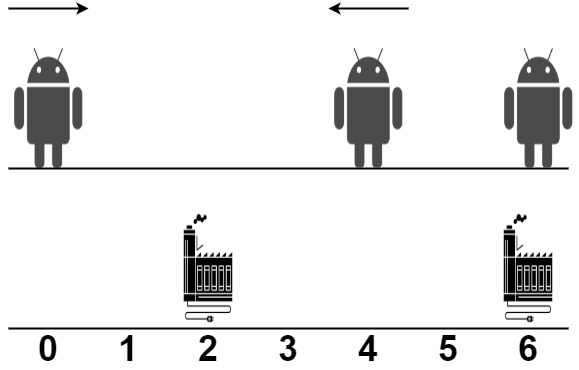
输入：robot = [0,4,6], factory = [[2,2],[6,2]]
输出：4
解释：如上图所示：
- 第一个机器人从位置 0 沿着正方向移动，在第一个工厂处维修。
- 第二个机器人从位置 4 沿着负方向移动，在第一个工厂处维修。
- 第三个机器人在位置 6 被第二个工厂维修，它不需要移动。
第一个工厂的维修上限是 2 ，它维修了 2 个机器人。
第二个工厂的维修上限是 2 ，它维修了 1 个机器人。
总移动距离是 |2 - 0| + |2 - 4| + |6 - 6| = 4 。没有办法得到比 4 更少的总移动距离。

思路

思路一

坐标离散化+二分+贪心

做虚拟比赛时我的思路是：坐标离散化+二分。

具体来说，就是先把所有机器人的坐标存在一个数组里，所有工厂的坐标存在一个数组里。然后对两个数组从小到大排序。随后从坐标最小的机器人开始枚举，每次决定当前机器人应该往左走还是往右走。

怎么决定呢？从当前机器人的位置，往左，往右，找到距离最近的2个工厂，比较2个工厂到机器人的距离，选择较小的那个工厂。

typedef long long LL;
class Solution {
public:
    
    vector<int> indexR, indexF;
    
    unordered_map<int, int> f; // 工厂下标 - 剩余可修理次数
    
    // x 是机器人的下标
    // 找到左侧第一个可用工厂的位置
    int findLeft(int x) {
        int l = 0, r = indexF.size() - 1;
        while (l < r) {
            int mid = l + r + 1>> 1;
            if (indexF[mid] <= x) l = mid;
            else r = mid - 1;
        }
        if (indexF[l] <= x) return l;
        return -1;
    }
    
    int findRight(int x) {
        int l = 0, r = indexF.size() - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (indexF[mid] >= x) r = mid;
            else l = mid + 1;
        }
        if (indexF[l] >= x) return l;
        return -1;
    }
    
    
    LL minimumTotalDistance(vector<int>& robot, vector<vector<int>>& factory) {
        for (auto& i : robot) indexR.push_back(i);
        for (auto& i : factory) {
            indexF.push_back(i[0]);
            f[i[0]] += i[1]; // 工厂的可修理次数
        }
        // 坐标离散化
        sort(indexR.begin(), indexR.end());
        sort(indexF.begin(), indexF.end());

        // 对每个robot, 找到最近的工厂
        LL ans = 0;
        for (int i = 0; i < indexR.size(); i++) {
            // 往左找, 往右找
            int l = findLeft(indexR[i]), r = findRight(indexR[i]);
            // x是最终决定的工厂
            int x = l != -1 ? l : -1;
            if (x == -1) x = r;
            else if (r != -1) {
                // 左右两侧都有可用工厂时, 优先选择距离更近的
                int dl = abs(indexF[l] - indexR[i]), dr = abs(indexF[r] - indexR[i]);
                if (dl < dr) x = l;
                else if (dl > dr) x = r;
                else x = l; // 选左边的
            }
            // 选好后, 计算距离
            LL d = abs(indexF[x] - indexR[i]);
            ans += d;
            // 将这个工厂的可用次数减去1
            // 若这个工厂剩余可用次数为0, 则从工厂下标数组中将其删除
            if (--f[indexF[x]] == 0) indexF.erase(indexF.begin() + x);
        }
        return ans;
    }
};

提交后WA了。来看一组错误数据：

[9,11,99,101]
[[10,1],[7,1],[14,1],[100,1],[96,1],[103,1]]

根据上面的代码，对这组数据进行模拟。可以发现我们的决策是这样的：

• 位于9的机器人，往右去位于10的工厂进行修理，移动1
• 位于11的机器人，往右去位于14的工厂进行修理，移动3
• 位于99的机器人，往右去位于100的工厂进行修理，移动1
• 位于101的机器人，往右去位于103的工厂进行修理，移动2

总的移动次数为1 + 3 + 1 + 2 = 7

而实际的最优解为6，其决策是（下面用R表示机器人，F表示工厂）

• R9去F7，移动2
• R11去F10，移动1
• R99去F100，移动1，
• R101去F103，移动2

总的移动次数是2 + 1 + 1 + 2 = 6

可以看到，我上面的策略是对每个机器人在当前状态下做出最优选择，但这样并不能保证达到最终的全局最优。

我这样尝试通过局部最优去得到全局最优的贪心策略是不可行的。

原因是当前的决策会对后续的决策产生影响，每一次决策之间不是互相独立的。

比如R9选择了F10，对于R9来说是最优选择，但这样的决策会使得R11只能选择F14，从而使得R9和R11的总移动次数为1 + 3 = 4；而如果R9稍微牺牲下自己，去选择F7，这样就能使得R11可以选择F10，从而使得R9和R11的总移动次数为2 + 1 = 3，反而更小了。

思路二

中心扩散

接下来我又有了这样的想法：以每个工厂作为中心，分别同时往左右两端进行扩散（对于每个工厂，维护一下其往左右两边扩散的半径，每个工厂，其半径每秒钟增长1）。

对于某个机器人，其一定会在某个时刻被某个工厂扩散出来的半径所覆盖，当某个机器人第一次被某个工厂扩散的半径所覆盖时，这个工厂就是与该机器人距离最近的且可用的工厂。当某个工厂扩散的半径刚好到达某个机器人时，若该工厂还有剩余维修次数，则将该工厂的维修次数减1，且把该机器人标记为已被维修。扩散终将结束，并且那时所有的机器人都会被覆盖掉。每个工厂都会尽可能的维修与自己距离更近的机器人。这样看来好像是一种可行的方法。

但是！有些情况无法被处理。比如某个工厂的可维修次数只有1，并且在某一时刻，恰好有2个机器人被该工厂的半径所覆盖，那么该工厂应该选择维修哪个机器人呢？这个是不太好判断的，因为还需要更多的额外信息。比如上面的样例，F10在第一秒钟时，其扩散出来的区间范围是[9, 11]，恰好到达了R9和R11，由于它只有1次可维修次数，此时它应该选择维修R9还是R11呢？此时需要看，如果不维修R9，那么R9被后来的工厂所覆盖的最短距离是多少；以及如果不维修R11，那么R11被后来的工厂所覆盖的最短距离是多少。如果R9被后来的工厂所覆盖的最短距离比R11的更短，那么应该选择不维修R9，维修R11。这个信息的计算可能会产生嵌套。

并且，由于整个坐标的值域很大，[-10^9, 10^9]，我们每次对所有工厂扩散1，则一个工厂最多需要扩散 10^9次，这样肯定就超时了。所以该思路最终没有走下去。

思路三

动态规划

很自然的，我们先对机器人和工厂的坐标，从小到大排个序。

随后，能观察到这样一个事实：假设有两个机器人Rx和Ry，设在最优解中，它们最终被送到的工厂分别是Fx和Fy。若两个机器人之间的坐标关系是 Rx <= Ry，那么一定有 Fx <= Fy。

也就是说，排完序后，从左往右的机器人，一定是依次被送到了从左往右的工厂里去维修。也就是说，从左往右遍历每个机器人时，是先将若干个机器人送到了第一个工厂，第一个工厂的维修次数用完后，又将若干个机器人送到第二个工厂，又将若干个机器人送到第三个工厂… (当然，这样描述其实并不准确，甚至是有问题的，但可以近似这样来理解)

先用反证法，证明一下这个结论。

不妨设 Rx < Ry，假设Rx是往左走，到达的Fx，接下来我们考虑Fy的位置，若Fy < Fx（违反上述结论时），如下图

那么Rx移动的距离是b，Ry移动的距离是a + b + c，Rx和Ry总的移动距离是a + 2b + c

此时如果交换一下，让Rx去Fy，让Ry去Fx，那么Rx的移动距离是a + b，Ry的移动距离是b + c，它俩的总移动距离是a + 2b + c，是不变的。

所以，只要存在Rx < Ry，且Fx > Fy的情况，我们总是能够做一下交换，而总的移动距离并不会变得更大。

所以，我们总是能够保证，对于机器人Rx <= Ry，最优解中一定有 Fx <= Fy。即两个机器人之间的坐标的前后关系，和它们最终选择的工厂的坐标的前后关系，是一致的。

于是我们就能够按上面所描述的，从左往右处理每个机器人，依次将机器人送到从左往右的工厂里去维修。

前i个工厂，一定是维修了前j个机器人的，不可能存在 前i个工厂，维修了[0, k]以及[k + x, j] 这些机器人，中间还有x个机器人没有被维修，这样的情况。

所以我们可以这样设置状态表示：dp[i][j]表示用前i个工厂，维修了前j个机器人时，机器人总的移动距离。

状态转移时，我们考虑第i个工厂。

第i个工厂

• 要么一个机器人都不维修
• 要么维修了[0, j]中，最右侧的连续若干个机器人（一定是维修了最右侧的若干个，而不是跳过最右侧去维修更左侧的机器人），

对于第二种情况，我们假设第i个工厂，维修了k个机器人，只需要枚举一下k的所有可能的取值，计算一下状态转移即可，状态转移的方程是：dp[i][j] = dp[i - 1][j - k] + cost[?]，其中的cost[?]表示这k个机器人到第i个工厂的距离之和。

最终的答案当然就是dp[n][m]，即使用全部的工厂，维修全部的机器人的距离之和。

typedef long long LL;
const LL INF = 1e13; // 由于此题的数据范围, 机器人最多有100个, 整个坐标值域最大为10^9, 所以将正无穷开为10^13
class Solution {
public:
    LL minimumTotalDistance(vector<int>& robot, vector<vector<int>>& factory) {
        int m = robot.size(), n = factory.size();
        sort(robot.begin(), robot.end());
        sort(factory.begin(), factory.end());
        vector<vector<LL>> dp(n + 1, vector<LL>(m + 1, INF));
        // 状态边界
        for (int i = 0; i <= n; i++) dp[i][0] = 0; // 维修0个机器人时, 距离全都为0
        // 开始转移
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                dp[i][j] = dp[i - 1][j]; // 第i个工厂, 1个机器人也不维修时
                LL sum = 0;
                // 枚举第i个工厂能维修的机器人的数量
                for (int k = 1; k <= min(factory[i - 1][1], j); k++) {
                    int idx = j - k; // 此次维修的机器人的坐标, 下标从0开始
                    sum += abs(robot[idx] - factory[i - 1][0]); // 累加距离之和
                    dp[i][j] = min(dp[i][j], dp[i - 1][j - k] + sum); // 状态转移
                }
            }
        }
        return dp[n][m];
    }
};

这道题目，最重要的是要推出，机器人之间的坐标前后关系，与它们选择的工厂的坐标前后关系，是一致的。只有具备这个条件，才能按照上述的思路进行状态的转移。

总结

T1是双指针模拟；T2是滑动窗口；T3是双指针+堆；T4是动态规划

这次周赛是在周日上午，由于前一周拔了牙，当天周日早上去医院拆线，所以这场周赛没有参加。后来做了下虚拟比赛，只做出3题，T4还差点思维。