一、单个样本的Logistic回归的梯度下降法
在本节中,我们学习如何计算偏导数来实现Logistic回归的梯度下降法。
我们将使用导数流程图来计算梯度。
首先回顾一下Logistic回归的公式
z = w T x + b z = w^Tx+b z=wTx+b
y ^ = a = σ ( z ) = 1 1 + e − z \widehat{y}=a = \sigma(z) = \frac 1 {1+e^{-z}} y =a=σ(z)=1+e−z1
L ( a , y ) = − ( y l o g ( a ) + ( 1 − y ) l o g ( 1 − a ) ) L(a,y)=-(ylog(a) +(1-y)log(1-a)) L(a,y)=−(ylog(a)+(1−y)log(1−a))
现在只考虑单个样本的情况
L
(
a
,
y
)
=
−
(
y
l
o
g
(
a
)
+
(
1
−
y
)
l
o
g
(
1
−
a
)
)
L(a,y)=-(ylog(a) +(1-y)log(1-a))
L(a,y)=−(ylog(a)+(1−y)log(1−a)),为Logistic的损失函数,a是Logistic回归的输出,y是样本的基本真值标签值。
现在写出该样本的偏导数流程图
假设样本只有两个,特征x1和x2,为了计算z,我们需要输出参数w1,w2和b,还有样本特征x1,x2,因此用来计算z的偏导数公式,
z
=
w
1
∗
x
1
+
w
2
∗
x
2
+
b
z=w1*x1+w2*x2+b
z=w1∗x1+w2∗x2+b,
y
^
=
a
=
σ
(
z
)
\hat y = a = \sigma(z)
y^=a=σ(z)是偏导数流程图的下一步,最后计算L(a,y).

因此,在逻辑回归中,我们需要做的是变换参数w和b的值,来最小化损失函数。
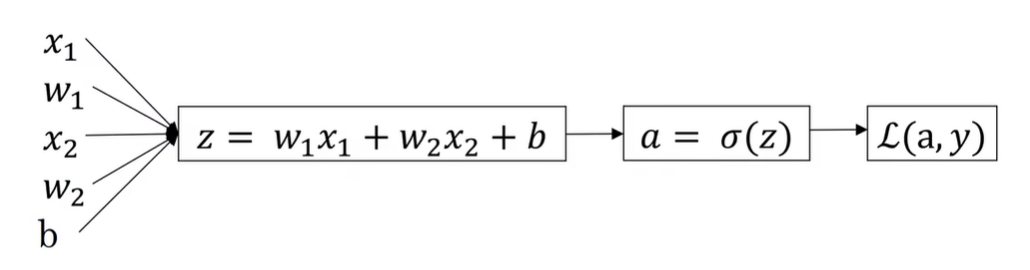
接下来我们讨论怎样向后计算偏导数,想要计算损失函数 L ( a , y ) L(a,y) L(a,y)的导数,首先我们要向前一步,先计算损失函数的导数 d L ( a , y ) d a \frac {dL(a,y)} {d a} dadL(a,y),即L关于变量a的导数,在代码中,我们用da来表示这个变量。如果你熟悉微积分的话,这个da的结果为 d L ( a , y ) d a = d a = − y a + 1 − y 1 − a \frac { dL(a,y)} {da} = d a = \frac {-y} a+\frac {1-y} {1-a} dadL(a,y)=da=a−y+1−a1−y,损失函数的导数计算公式就是这样,计算关于变量a的导数,就是这个式子。
现在计算出da,最终结果关于变量a的导数,现在可以在向后一步,计算dz,dz是代码中的变量名,dz是损失函数关于z的导数,
d
z
=
d
L
d
z
=
d
L
(
a
,
y
)
d
z
=
a
−
y
dz = \frac {dL} {dz} = \frac {dL(a,y)} {dz} = a-y
dz=dzdL=dzdL(a,y)=a−y;其中
d
L
d
z
=
d
L
(
a
,
y
)
d
a
∗
d
a
d
z
\frac {dL} {dz} = \frac {dL(a,y)} {da}* \frac {da} {dz}
dzdL=dadL(a,y)∗dzda,其中
d
a
d
z
=
a
∗
(
1
−
a
)
\frac {da} {dz} = a*(1-a)
dzda=a∗(1−a),这个推导的过程,即“链式法则”。
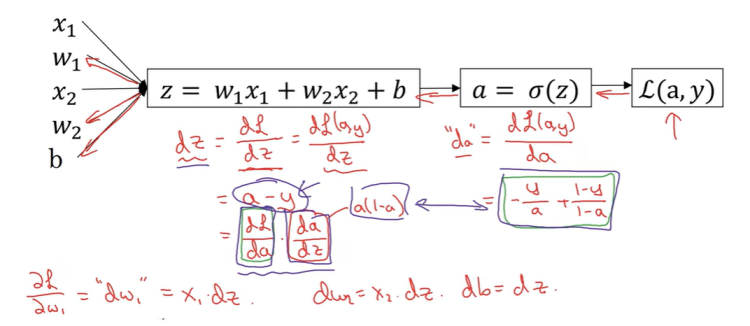
现在后向传播的最后一步,计算看看w和b需要如何变化,特别的关于w1的导数 d L d w 1 = d w 1 = x 1 ∗ d z \frac {dL} {dw1} = dw1 = x1 *dz dw1dL=dw1=x1∗dz,同样的 d L d w 2 = d w 2 = x 2 ∗ d z \frac {dL} {dw2} = dw2 = x2 *dz dw2dL=dw2=x2∗dz, d L d b = d b = d z \frac {dL} {db} = db = dz dbdL=db=dz。
因此关于单个样本的梯度下降法,你说需要做的就是这些事情。使用上面的公式计算dz、dw1、dw2、db。
更新
w
1
=
w
1
−
α
∗
d
w
1
;
w
2
=
w
1
−
α
∗
d
w
2
;
b
=
b
−
α
∗
d
b
w1= w1 - α*dw1;w2= w1 - α*dw2;b = b - α*db
w1=w1−α∗dw1;w2=w1−α∗dw2;b=b−α∗db。这是单个样本实例的一次梯度更新的步骤。
详细的推导过程
z = w T x + b z = w^Tx+b z=wTx+b
y ^ = a = σ ( z ) = 1 1 + e − z \widehat{y}=a = \sigma(z) = \frac 1 {1+e^{-z}} y =a=σ(z)=1+e−z1
L
(
a
,
y
)
=
−
(
y
l
o
g
(
a
)
+
(
1
−
y
)
l
o
g
(
1
−
a
)
)
L(a,y)=-(ylog(a) +(1-y)log(1-a))
L(a,y)=−(ylog(a)+(1−y)log(1−a))
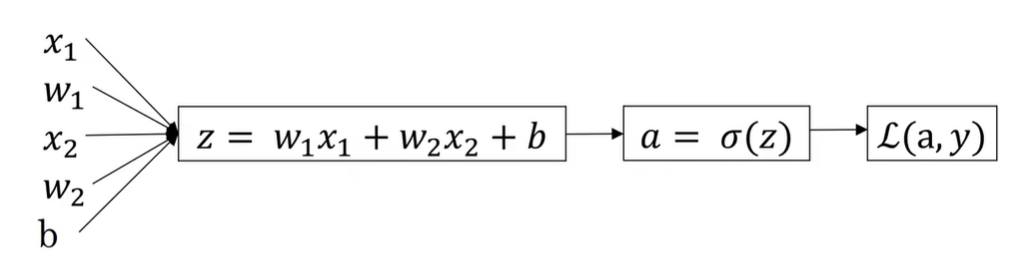
∂ L ( a , y ) d a = − y a + ( 1 − y 1 − a ) \frac {\partial L(a,y)} {da} = -\frac y a + (\frac {1-y} {1-a}) da∂L(a,y)=−ay+(1−a1−y)
= a − y a ( 1 − a ) =\frac {a-y} {a(1-a)} =a(1−a)a−y,其中 ∂ L ( a , y ) d a \frac {\partial L(a,y)} {da} da∂L(a,y)就是L(a,y)关于a的偏导数。
∂ L ( a , y ) d z = ∂ L ( a , y ) d a d a d z \frac {\partial L(a,y)} {dz} = \frac {\partial L(a,y)} {da} \frac {da} {dz} dz∂L(a,y)=da∂L(a,y)dzda,其中
d a d z = e − z ( 1 + e − z ) 2 \frac {da} {dz} =\frac {e^{-z}} {(1+e^{-z})^2} dzda=(1+e−z)2e−z
= 1 + e − z − 1 ( 1 + e − z ) 2 =\frac {1+e^{-z} - 1} {(1+e^{-z})^2} =(1+e−z)21+e−z−1
= 1 1 + e − z − 1 ( 1 + e − z ) 2 =\frac 1 {1+e^{-z}} - \frac 1 {(1+e^{-z})^2} =1+e−z1−(1+e−z)21
= a − a 2 = a ( 1 − a ) =a - a^2 = a(1-a) =a−a2=a(1−a)
因此,推导出, ∂ L ( a , y ) d z = a − y \frac {\partial L(a,y)} {dz} = a - y dz∂L(a,y)=a−y,代码中用dz表示。
∂ L ( a , y ) d w 1 = ∂ L ( a , y ) d a ∗ d a d z ∗ d z d w 1 = d w 1 = x 1 ∗ d z \frac {\partial L(a,y)} {dw1} = \frac {\partial L(a,y)} {da} *\frac {da} {dz}* \frac {dz} {dw1} = dw1 = x1*dz dw1∂L(a,y)=da∂L(a,y)∗dzda∗dw1dz=dw1=x1∗dz,代码中,用dw1表示
∂ L ( a , y ) d w 2 = ∂ L ( a , y ) d a ∗ d a d z ∗ d z d w 2 = d w 2 = x 2 ∗ d z \frac {\partial L(a,y)} {dw2} = \frac {\partial L(a,y)} {da} *\frac {da} {dz}* \frac {dz} {dw2} = dw2 = x2*dz dw2∂L(a,y)=da∂L(a,y)∗dzda∗dw2dz=dw2=x2∗dz,代码中,用dw2表示
∂ L ( a , y ) d b = ∂ L ( a , y ) d a ∗ d a d z ∗ d z d b = d b = d z \frac {\partial L(a,y)} {db} = \frac {\partial L(a,y)} {da} *\frac {da} {dz}* \frac {dz} {db} = db = dz db∂L(a,y)=da∂L(a,y)∗dzda∗dbdz=db=dz,代码中,用db表示
对参数w和b进行更新,其中α是学习率
w
1
=
w
1
−
α
∗
d
w
1
w1= w1 - α*dw1
w1=w1−α∗dw1
w
2
=
w
1
−
α
∗
d
w
2
w2= w1 - α*dw2
w2=w1−α∗dw2
b
=
b
−
α
∗
d
b
b = b - α*db
b=b−α∗db
二、m个样本的Logistic回归的梯度下降法
首先,我们需要记住关于成本函数J(w,b)的定义
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
L
(
a
(
i
)
,
y
(
i
)
)
J(w,b) = \frac 1 m \sum_{i=1}^m{L(a^{(i)},y^{(i)})}
J(w,b)=m1∑i=1mL(a(i),y(i))
a
(
i
)
=
y
^
(
i
)
=
σ
(
z
(
i
)
)
=
σ
(
w
T
x
(
i
)
+
b
)
a^{(i)} = \hat{y}^{(i)} = \sigma(z^{(i)}) = \sigma{(w^Tx^{(i)}+b)}
a(i)=y^(i)=σ(z(i))=σ(wTx(i)+b)
全局成本函数是一个求和,实际上是1到m项,损失函数和的平均。
它表明全局成本函数对w1的导数,也同样是各项损失函数对w1导数的平均。
∂
∂
w
1
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
∂
∂
w
1
L
(
a
(
i
)
,
y
(
i
)
)
\frac {\partial} {\partial w1} J(w,b) = \frac 1 m \sum_{i = 1}^m\frac {\partial} {\partial w1} L(a^{(i)},y^{(i)})
∂w1∂J(w,b)=m1∑i=1m∂w1∂L(a(i),y(i)),其中
∂
∂
w
1
L
(
a
(
i
)
,
y
(
i
)
)
=
d
w
1
(
i
)
=
(
x
(
i
)
,
y
(
i
)
)
\frac {\partial} {\partial w1} L(a^{(i)},y^{(i)}) = dw1^{(i)} = (x^{(i)},y^{(i)})
∂w1∂L(a(i),y(i))=dw1(i)=(x(i),y(i)),即对单个训练样本进行计算,所以真正需要做的是计算这些导数,如我们之前的训练样本上做的,并且求平均,会得到全局梯度值,你可以将它直接应用到梯度下降算法中。
让我们将其使用到一个具体的算法中。
J = 0;dw1 = 0;dw2 = 0;db = 0
For i = 1 to m
z
(
i
)
=
w
T
x
(
i
)
+
b
z^{(i)} = w^Tx^{(i)} + b
z(i)=wTx(i)+b
a
(
i
)
=
σ
(
z
(
i
)
)
a^{(i)} = \sigma(z^{(i)})
a(i)=σ(z(i))
J
+
=
−
[
y
(
i
)
l
o
g
a
(
i
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
a
(
i
)
)
]
J+=-[y^{(i)}loga^{(i)}+(1-y^{(i)})log(1-a^{(i)})]
J+=−[y(i)loga(i)+(1−y(i))log(1−a(i))]
d
z
(
i
)
=
a
(
i
)
−
y
(
i
)
dz^{(i)} = a^{(i)} - y^{(i)}
dz(i)=a(i)−y(i)
d
w
1
+
=
x
1
(
i
)
d
z
(
i
)
dw1+=x1^{(i)}dz^{(i)}
dw1+=x1(i)dz(i) 目前特征2个,n=2
d
w
2
+
=
x
2
(
i
)
d
z
(
i
)
dw2+=x2^{(i)}dz^{(i)}
dw2+=x2(i)dz(i)
d
b
+
=
d
z
(
i
)
db +=dz^{(i)}
db+=dz(i)
J/=m
dw1/=m
dw2/=m
db/=m
其中,
d
w
1
=
∂
J
∂
w
1
dw1 = \frac {\partial J} {\partial w1}
dw1=∂w1∂J
w
1
:
=
w
1
−
α
d
w
1
w1:= w1 - \alpha dw1
w1:=w1−αdw1
w
2
:
=
w
2
−
α
d
w
2
w2:= w2 - \alpha dw2
w2:=w2−αdw2
b
:
=
b
−
α
d
b
b:= b - \alpha db
b:=b−αdb
上述代码只应用了一次梯度下降法,因此,你需要重复上述内容很多次,以应用多次梯度下降。
上述计算中有两个缺点,即我们需要编写两个for循环,第一个for循环是遍历m个训练样本的小循环,第二个for循环是遍历所有特征的for循环,这个例子中,我们有两个特征,所以n等于2,n_x等于2,但是如果你有更多特征,你就需要一个for循环,来遍历所有的n个特征,当你应用深度学习算法,你会发现,在代码中显式的使用for循环,会使算法效率很低。同时在深度学习领域,会有越来越大的数据集,所以能够应用你的算法,完全不用显式for循环的话,会是重要的,会帮助你处理更大的数据集,有一门向量化技术,帮助你的代码,摆脱这些显式的for循环。在深度学习的早期,向量化技术有时候用来加速运算是非常棒的,在深度学习时代,用向量化来摆脱for循环已经变得相当重要。