本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-Ch01自动控制原理
- 1. 开环系统与闭环系统Open/Closed Loop System
- 1.1 EG1: 烧水与控温水壶
- 1.2 EG2: 蓄水与最终水位
- 1.3 闭环控制系统
- 2. 稳定性分析Stability
- 2.1 序言
- 2.2 稳定的分类
- 2.3 稳定的对象
- 2.4 稳定的系统
- 2.5 系统稳定性的讨论
- 2.6 补充内容——Transfer Function(传递函数) - nonzero Initial Condition(非零初始条件)
- 3. 燃烧卡路里-系统分析实例
- 3.1 数学模型
- 3.2 比例控制 Proprotional Control
- 4 终值定理和稳态误差Final Value Theorem & Steady State Error
- 5 比例积分控制器Proportional-Intefral Controller
- 6 根轨迹Root locus
- 6.1 根的作用
- 6.2 手绘技巧
- 6.3 分离点/汇合点&根轨迹的几何性质
- 7 Lead Compensator超前补偿器(调节根轨迹)
- 7.1 Plot Rootlocus 绘制根轨迹
- 7.2 System Performance 系统表现
- 7.3 改善/加快收敛速度
- 7.4 超前补偿器 Lead Comperastor
- 8 Lag Compensator滞后补偿器
- 9 PID控制器
- 10 奈奎斯特稳定性判据-Nyquist Stability Criterion
1. 开环系统与闭环系统Open/Closed Loop System
1.1 EG1: 烧水与控温水壶

1.2 EG2: 蓄水与最终水位

h
˙
=
q
i
n
A
−
g
h
A
R
\dot{h}=\frac{q_{in}}{A}-\frac{gh}{AR}
h˙=Aqin−ARgh
设
A
=
1
A=1
A=1. 目标:
h
=
x
→
x
d
h=x\rightarrow x_d
h=x→xd —— 保持液面高度
x
d
=
C
R
g
,
C
=
x
d
g
R
=
u
,
G
(
s
)
=
1
S
+
g
R
x_d=\frac{CR}{g},C=\frac{x_dg}{R}=u,G\left( s \right) =\frac{1}{S+\frac{g}{R}}
xd=gCR,C=Rxdg=u,G(s)=S+Rg1
1.3 闭环控制系统

X
=
D
G
1
+
H
D
G
V
X=\frac{DG}{1+HDG}V
X=1+HDGDGV
2. 稳定性分析Stability
2.1 序言

2.2 稳定的分类

2.3 稳定的对象
明确分析对象

e
=
T
a
r
g
e
t
−
θ
e=Target\,\,-\,\,\theta
e=Target−θ
Does the error converge to zero or not —— error dynamics stable or not
2.4 稳定的系统
Open loop 开环

Closed loop 闭环

EG1:

EG2:

2.5 系统稳定性的讨论


2.6 补充内容——Transfer Function(传递函数) - nonzero Initial Condition(非零初始条件)

3. 燃烧卡路里-系统分析实例
3.1 数学模型


3.2 比例控制 Proprotional Control


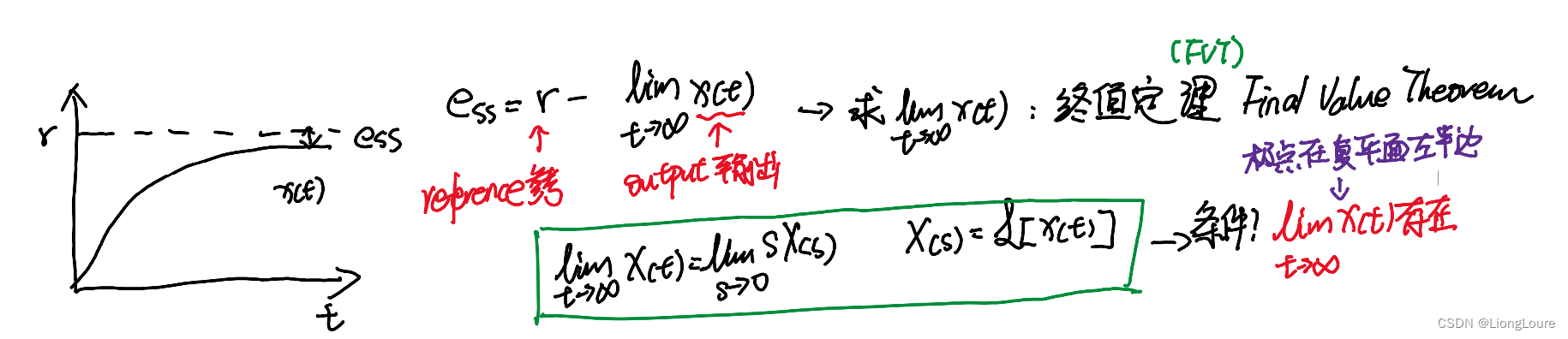
4 终值定理和稳态误差Final Value Theorem & Steady State Error



5 比例积分控制器Proportional-Intefral Controller
消除稳态误差——设计新的控制器


6 根轨迹Root locus
6.1 根的作用
G
(
s
)
=
s
+
3
s
2
+
2
s
+
4
G\left( s \right) =\frac{s+3}{s^2+2s+4}
G(s)=s2+2s+4s+3
Matlab可绘制 riocus(g)
掌握根的变化规律 , 设计控制器,补偿器 : Compentator Lead Lag…
根 —— 极点
- 一阶系统

- 二阶系统


- 三阶系统


6.2 手绘技巧
Matlab可以精确绘制——手绘——掌握根的变化规律——设计控制器
根轨迹的基本形式

根轨迹研究的是: 当
K
K
K从0到
+
∞
+\infty
+∞时,闭环系统根(极点)位置的变化规律
1 + K G ( s ) = 0 , G ( s ) = N ( s ) D ( s ) = ( s − z 1 ) ( s − z 2 ) ⋯ ( s − z m ) ( s − p 1 ) ( s − p 2 ) ⋯ ( s − p n ) 1+KG\left( s \right) =0,G\left( s \right) =\frac{N\left( s \right)}{D\left( s \right)}=\frac{\left( s-z_1 \right) \left( s-z_2 \right) \cdots \left( s-z_{\mathrm{m}} \right)}{\left( s-p_1 \right) \left( s-p_2 \right) \cdots \left( s-p_{\mathrm{n}} \right)} 1+KG(s)=0,G(s)=D(s)N(s)=(s−p1)(s−p2)⋯(s−pn)(s−z1)(s−z2)⋯(s−zm)
其中,
z
1
⋯
z
m
z_1\cdots z_{\mathrm{m}}
z1⋯zm 为零点 Zeros
⊙
\odot
⊙ ,
p
1
⋯
p
n
p_1\cdots p_{\mathrm{n}}
p1⋯pn 为极点 Poles
×
\times
×
规则1 :共有
n
n
n条根轨迹, 若
n
>
m
n>m
n>m;共有
m
m
m条根轨迹,若
m
>
n
m>n
m>n;
⇐
max
{
m
,
n
}
\Leftarrow \max \left\{ m,n \right\}
⇐max{m,n}
规则2 :若
m
=
n
m=n
m=n,随着
K
K
K从
0
→
∞
0\rightarrow \infty
0→∞ , 根轨迹从
G
(
s
)
G\left( s \right)
G(s)的极点向零点移动:
1
+
K
G
(
s
)
=
0
⇒
D
(
s
)
+
K
N
(
s
)
=
0
1+KG\left( s \right) =0\Rightarrow D\left( s \right) +KN\left( s \right) =0
1+KG(s)=0⇒D(s)+KN(s)=0 ,
K
→
0
K\rightarrow 0
K→0 时
D
(
s
)
=
0
D\left( s \right) =0
D(s)=0(极点);
K
→
∞
K\rightarrow \infty
K→∞ 时
N
(
s
)
=
0
N\left( s \right) =0
N(s)=0 (零点)
规则3:实轴上的根轨迹存在于从右向左第奇数个极点/零点的左边
规则4:若附属跟存在,则一定是共轭的,所以根轨迹通过实轴对称
规则5:若
n
>
m
n>m
n>m , 则有
n
−
m
n-m
n−m个极点指向无穷;若
m
>
n
m>n
m>n , 则有
m
−
n
m-n
m−n条根轨迹从无穷指向零点
规则6:根轨迹延渐近线移动,渐近线与实轴的交点
σ
=
∑
p
−
∑
z
n
−
m
\sigma =\frac{\sum{p}-\sum{z}}{n-m}
σ=n−m∑p−∑z ,渐近线与实轴的夹角
θ
=
2
q
+
1
n
−
m
π
,
q
=
0
,
1
,
.
.
.
,
n
−
m
−
1
/
m
−
n
−
1
\theta =\frac{2q+1}{n-m}\pi ,q=0,1,...,n-m-1/m-n-1
θ=n−m2q+1π,q=0,1,...,n−m−1/m−n−1

6.3 分离点/汇合点&根轨迹的几何性质
以 2nd-order system 为例:

Properties of Root locus

7 Lead Compensator超前补偿器(调节根轨迹)

7.1 Plot Rootlocus 绘制根轨迹
G
(
s
)
=
1
s
(
s
+
2
)
G\left( s \right) =\frac{1}{s\left( s+2 \right)}
G(s)=s(s+2)1

7.2 System Performance 系统表现
输入Input —— δ ( t ) \delta \left( t \right) δ(t) 单位冲激
-
K
K
K 较小时,
p
1
,
p
2
p_1,p_2
p1,p2 :
x
(
t
)
=
c
1
e
p
1
t
+
c
2
e
p
2
t
,
p
1
<
0
,
p
2
<
0
x\left( t \right) =c_1e^{p_1t}+c_2e^{p_2t},p_1<0,p_2<0
x(t)=c1ep1t+c2ep2t,p1<0,p2<0

-
K
K
K 较大时,根在复平面:
p
1
,
p
2
p_1,p_2
p1,p2 :
x
(
t
)
=
c
e
−
t
sin
ω
n
t
x\left( t \right) =ce^{-t}\sin \omega _{\mathrm{n}}t
x(t)=ce−tsinωnt - 无论如何改变
K
K
K值,都无法改变收敛速度
-
7.3 改善/加快收敛速度
——改变根轨迹,希望根在
−
2
+
2
3
-2+2\sqrt{3}
−2+23
G
(
s
)
=
1
s
(
s
+
2
)
G\left( s \right) =\frac{1}{s\left( s+2 \right)}
G(s)=s(s+2)1
在根轨迹上的点满足:
∠
K
G
(
s
)
=
−
π
\angle KG\left( s \right) =-\pi
∠KG(s)=−π (零点到根的夹角和 - 极点到根的夹角和)
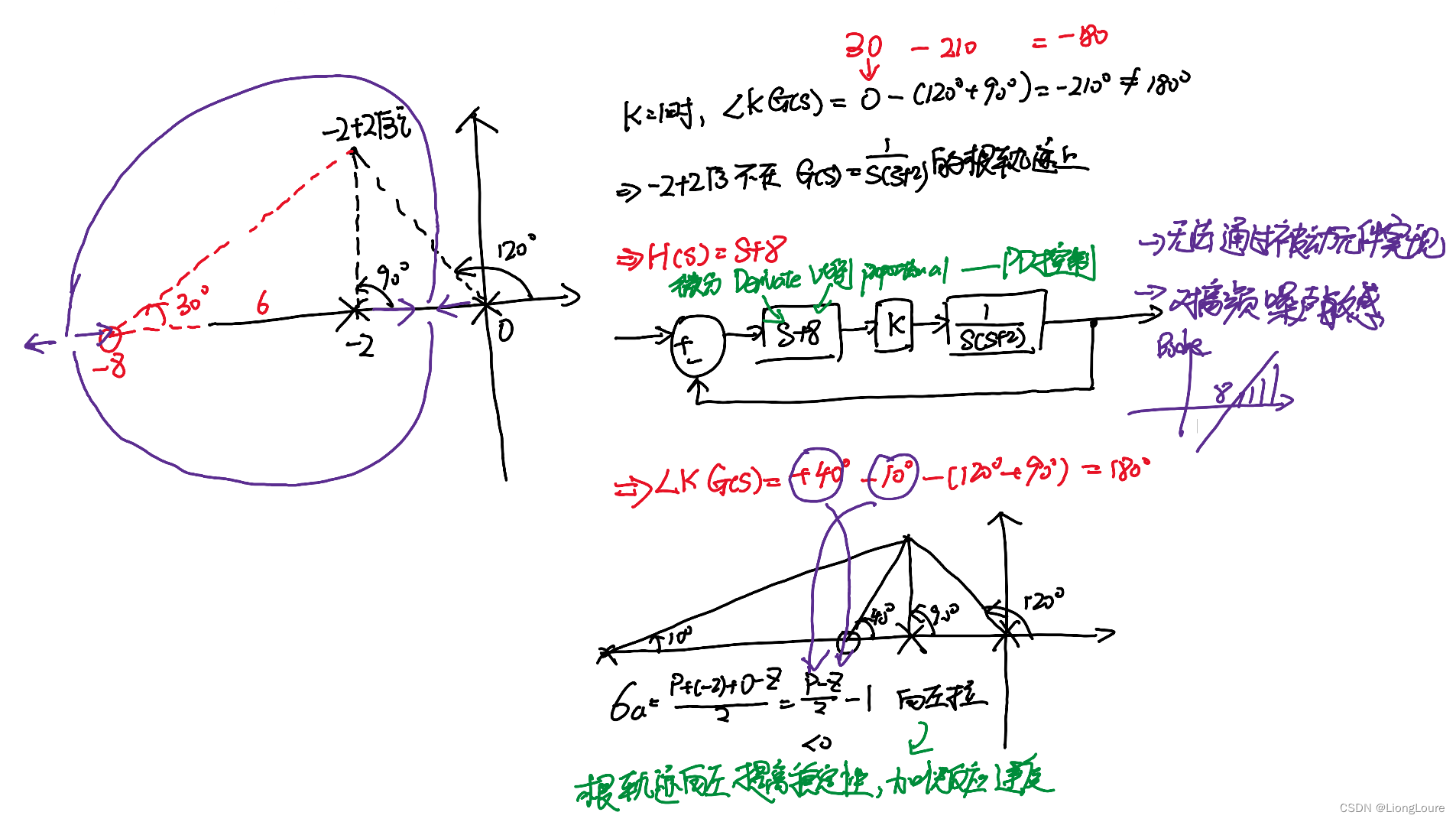
7.4 超前补偿器 Lead Comperastor
H
(
s
)
=
s
−
z
s
−
p
,
∥
z
∥
<
∥
p
∥
H\left( s \right) =\frac{s-z}{s-p},\left\| z \right\| <\left\| p \right\|
H(s)=s−ps−z,∥z∥<∥p∥

8 Lag Compensator滞后补偿器
从稳态误差入手(steady state Error)

误差 Error :
E
(
s
)
=
R
(
s
)
−
X
(
s
)
=
R
(
s
)
−
E
(
s
)
⋅
K
G
(
s
)
⇒
E
(
s
)
(
1
+
K
G
(
s
)
)
=
R
(
s
)
⇒
E
(
s
)
=
1
1
+
K
G
(
s
)
R
(
s
)
=
R
(
s
)
1
1
+
K
N
(
s
)
D
(
s
)
=
1
s
1
1
+
K
N
(
s
)
D
(
s
)
E\left( s \right) =R\left( s \right) -X\left( s \right) =R\left( s \right) -E\left( s \right) \cdot KG\left( s \right) \Rightarrow E\left( s \right) \left( 1+KG\left( s \right) \right) =R\left( s \right) \Rightarrow E\left( s \right) =\frac{1}{1+KG\left( s \right)}R\left( s \right) =R\left( s \right) \frac{1}{1+K\frac{N\left( s \right)}{D\left( s \right)}}=\frac{1}{s}\frac{1}{1+K\frac{N\left( s \right)}{D\left( s \right)}}
E(s)=R(s)−X(s)=R(s)−E(s)⋅KG(s)⇒E(s)(1+KG(s))=R(s)⇒E(s)=1+KG(s)1R(s)=R(s)1+KD(s)N(s)1=s11+KD(s)N(s)1
单位阶跃unit step :
R
(
s
)
=
1
s
R\left( s \right) =\frac{1}{s}
R(s)=s1
稳态误差Steady State Error——FVT终值定理
e
s
s
=
lim
t
→
∞
e
(
t
)
=
lim
s
→
o
s
E
(
s
)
=
lim
s
→
o
s
⋅
1
s
1
1
+
K
N
(
s
)
D
(
s
)
=
1
1
+
K
N
(
0
)
D
(
0
)
=
D
(
0
)
D
(
0
)
+
K
N
(
0
)
ess=\underset{t\rightarrow \infty}{\lim}e\left( t \right) =\underset{s\rightarrow o}{\lim}sE\left( s \right) =\underset{s\rightarrow o}{\lim}s\cdot \frac{1}{s}\frac{1}{1+K\frac{N\left( s \right)}{D\left( s \right)}}=\frac{1}{1+K\frac{N\left( 0 \right)}{D\left( 0 \right)}}=\frac{D\left( 0 \right)}{D\left( 0 \right) +KN\left( 0 \right)}
ess=t→∞lime(t)=s→olimsE(s)=s→olims⋅s11+KD(s)N(s)1=1+KD(0)N(0)1=D(0)+KN(0)D(0)


9 PID控制器
P —— Proportional
I —— Integral
D —— Derivative
- 当前误差/过去误差/误差的变化趋势

- K p ⋅ e K_{\mathrm{p}}\cdot e Kp⋅e:比例增益——当前误差
- K I ⋅ ∫ e d t K_{\mathrm{I}}\cdot \int{e}dt KI⋅∫edt:积分增益——过去误差-积累
-
K
D
⋅
d
e
d
t
K_{\mathrm{D}}\cdot \frac{\mathrm{d}e}{\mathrm{d}t}
KD⋅dtde :微分增益——变化趋势 (对噪音敏感)
L [ u ] = L [ K P ⋅ e + K I ⋅ ∫ e d t + K D ⋅ d e d t ] ⇒ U ( s ) = ( K P + K I 1 s + K D s ) ⋅ E ( s ) \mathcal{L} \left[ u \right] =\mathcal{L} \left[ K_{\mathrm{P}}\cdot e+K_{\mathrm{I}}\cdot \int{e}\mathrm{d}t+K_{\mathrm{D}}\cdot \frac{\mathrm{d}e}{\mathrm{d}t} \right] \Rightarrow U\left( s \right) =\left( K_{\mathrm{P}}+K_{\mathrm{I}}\frac{1}{s}+K_{\mathrm{D}}s \right) \cdot E\left( s \right) L[u]=L[KP⋅e+KI⋅∫edt+KD⋅dtde]⇒U(s)=(KP+KIs1+KDs)⋅E(s)
PID
PD控制:提高稳定性,改善瞬态
PI控制:改善稳态误差
10 奈奎斯特稳定性判据-Nyquist Stability Criterion


Cauchy’s Argument Priciple 柯西幅角原理

结论: s s s平面内顺时针画一条闭合曲线 A A A, B B B曲线是 A A A通过 F ( s ) F(s) F(s)后在 F ( s ) F(s) F(s)平面上的映射, A A A曲线每包含一个 F ( s ) F(s) F(s)的零点(极点), B B B曲线就绕 ( 0 , 0 ) (0,0) (0,0)点顺时针(逆时针)一圈