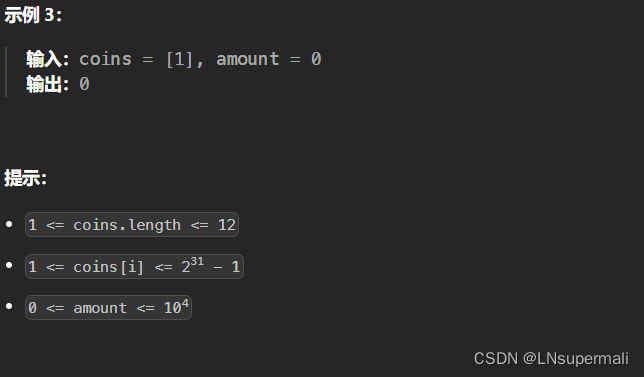
Problem: 322. 零钱兑换

题目描述

思路

该题目可以归纳为完全背包问题，最少需要多少物品能填满背包。该类问题大体思路如下

状态：

int dp[$n$][$w+1$] (其中$n$表示有$n$个物品，$w$表示背包最大重量为$w$),记录每个阶段可达重量对应的最少物品个数；

状态转移方程：

(i, j) 这个状态可能从(i - 1, j),(i - 1, j - weight[i]), (i - 1, j - 2weight[i]）,…(i - 1, j - kweight[i])转移过来（其中weight[i]表示物品的重量） dp[i][j] = Math.min(dp[i-1][j], dp[i-1][j-weight[i]] + 1, dp[i-1][j -2weight[i]] + 2， dp[i-1][j - kweight[i]] + k);

解题方法

1.定义一个int类型的二维数组dp[][]记录每个阶段可达数额对应的最少硬币个数（行数为coins数组的长度，列数为amount + 1）;
2.初始化数组dp将每一个位置值设为整形数最大值（Integer.MAX_VALUE）
3.初始化dp[][]第一行状态（循环范围c从0~amount/coins[0],并且dp[0][c*coins[0]] = c）
4.从dp[][]的第一行起开始动态转移，每次计算当前剩余可凑的数值（int k = j / coins[i];），同时判断可用于转换的上一状态是否小于当前状态dp[i - 1][j - c * coins[i]] + c < dp[i][j]
5.返回dp数组中最后的状态

复杂度

时间复杂度:

$O(n\cdot amount\cdot k)$ 其中$n$为coins数组的长度 $amount$为给定的数 $k$为当前剩余最大金额数

空间复杂度:

$O(n\cdot amount)$

Code

class Solution {
    /**
     * Returns the minimum number of coins for a given amount
     * (Complete knapsack problem)
     *
     * @param coins  Given array
     * @param amount Given number
     * @return int
     */
    public int coinChange(int[] coins, int amount) {
        int n = coins.length;
        //After deciding on the ith coin,
        // the minimum number of coins dp[i][j] is needed to make up the sum j.
        int[][] dp = new int[n][amount + 1];
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j <= amount; ++j) {
                dp[i][j] = Integer.MAX_VALUE;
            }
        }
        //Initialize the state of the first row
        for (int c = 0; c <= amount / coins[0]; ++c) {
            dp[0][c * coins[0]] = c;
        }
        for (int i = 1; i < n; ++i) {
            for (int j = 0; j <= amount; ++j) {
                //The maximum number of remaining loads
                 
                for (int c = 0; c <= k; ++c) {
                    if (dp[i - 1][j - c * coins[i]] != Integer.MAX_VALUE &&
                            dp[i - 1][j - c * coins[i]] + c < dp[i][j]) {
                        dp[i][j] = dp[i - 1][j - c * coins[i]] + c;
                    }
                }
            }
        }
        if (dp[n - 1][amount] == Integer.MAX_VALUE) {
            return -1;
        }
        return dp[n - 1][amount];
    }
}