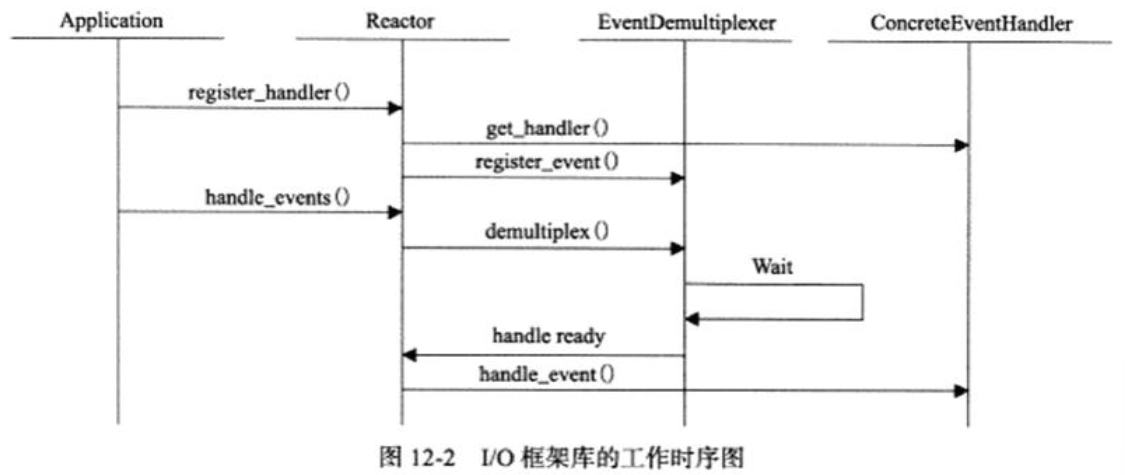
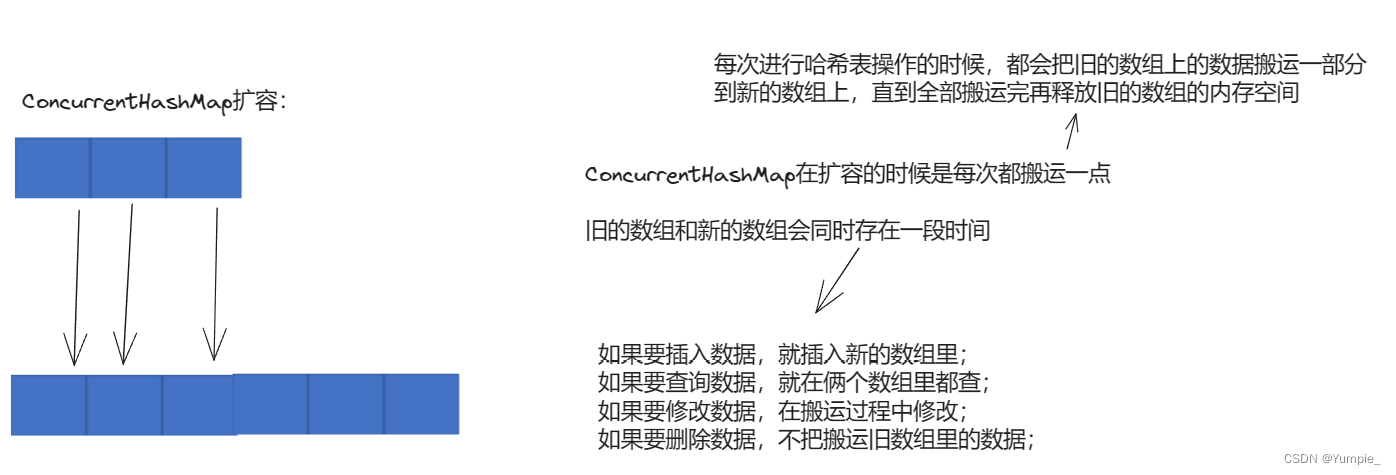
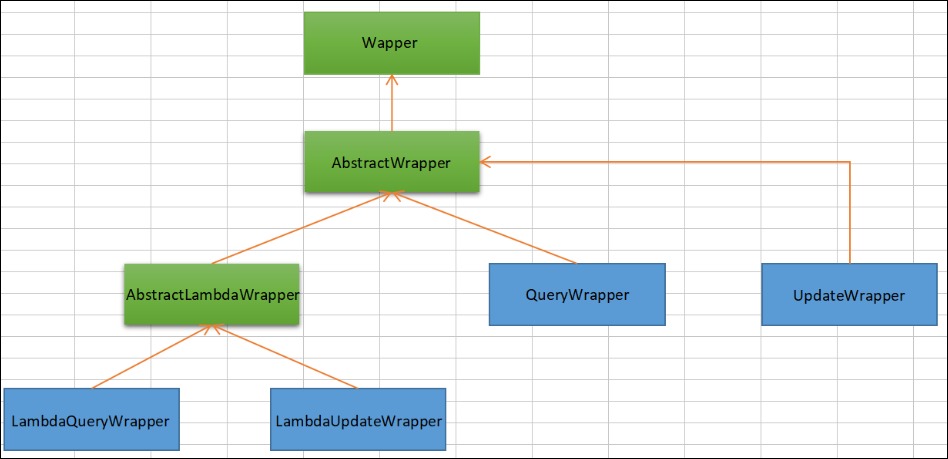
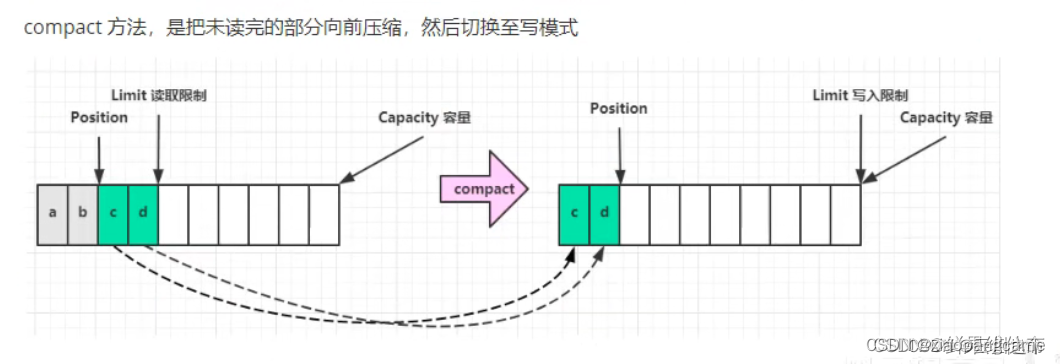
1 文本格式

using System;

namespace Legalsoft.Truffer
{
    public abstract class Fred2
    {
        public readonly double a;
        public readonly double b;
        public readonly int n;
        public double[] t;
        public double[] f;
        public double[] w;

        public abstract double g(double x);
        public abstract double ak(double x, double t);

        public Fred2(double aa, double bb, int nn)
        {
            this.a = aa;
            this.b = bb;
            this.n = nn;
            this.t = new double[n];
            this.f = new double[n];
            this.w = new double[n];
            double[,] omk = new double[n, n];
            GaussianWeights.gauleg(a, b, t, w);
            for (int i = 0; i < n; i++)
            {
                for (int j = 0; j < n; j++)
                {
                    //omk[i, j] = (double)(i == j) - ak(t[i], t[j]) * w[j];
                    omk[i, j] = (i == j ? 1 : 0) - ak(t[i], t[j]) * w[j];
                }
                f[i] = g(t[i]);
            }
            LUdcmp alu = new LUdcmp(omk);
            alu.solve( f, f);
        }

        public double fredin(double x)
        {
            double sum = 0.0;
            for (int i = 0; i < n; i++)
            {
                sum += ak(x, t[i]) * w[i] * f[i];
            }
            return g(x) + sum;
        }
    }
}
 

2 代码格式

using System;

namespace Legalsoft.Truffer
{
    public abstract class Fred2
    {
        public readonly double a;
        public readonly double b;
        public readonly int n;
        public double[] t;
        public double[] f;
        public double[] w;

        public abstract double g(double x);
        public abstract double ak(double x, double t);

        public Fred2(double aa, double bb, int nn)
        {
            this.a = aa;
            this.b = bb;
            this.n = nn;
            this.t = new double[n];
            this.f = new double[n];
            this.w = new double[n];
            double[,] omk = new double[n, n];
            GaussianWeights.gauleg(a, b, t, w);
            for (int i = 0; i < n; i++)
            {
                for (int j = 0; j < n; j++)
                {
                    //omk[i, j] = (double)(i == j) - ak(t[i], t[j]) * w[j];
                    omk[i, j] = (i == j ? 1 : 0) - ak(t[i], t[j]) * w[j];
                }
                f[i] = g(t[i]);
            }
            LUdcmp alu = new LUdcmp(omk);
            alu.solve( f, f);
        }

        public double fredin(double x)
        {
            double sum = 0.0;
            for (int i = 0; i < n; i++)
            {
                sum += ak(x, t[i]) * w[i] * f[i];
            }
            return g(x) + sum;
        }
    }
}