haha~
最近在准备数学竞赛,好久没有发布笔记啦,今天就来一波高数里常用的定理吧,不全面的话后续会更新哒~
-
费马定理:对于一个函数的局部极值点,如果导数存在,那么导数在该点处必须为零,即
f'(x)=0。 -
罗尔定理:如果函数 f(x) 在闭区间 [a, b] 上满足以下三个条件:(i) 在 [a, b] 上连续;(ii) 在 (a, b) 上可导;(iii) f(a) = f(b),那么存在至少一个 c ∈ (a, b),使得
f'(c) = 0。 -
界值定理:假设函数 f(x) 在闭区间 [a, b] 上连续,并且 f(a) 和 f(b) 的符号不同(即 f(a) * f(b) < 0)。那么对于任意处于 f(a) 和 f(b) 之间的实数 k,存在至少一个实数 c ∈ (a, b),使得
f(c) = k。 -
.零点定理:如果函数 f(x) 在区间 [a, b] 上连续,并且 f(a) 和 f(b) 的符号不同(即
f(a) * f(b) < 0),那么在开区间 (a, b) 内至少存在一个实数 c,使得f(c) = 0。 -
拉格朗日中值定理:如果函数 f(x) 在闭区间 [a, b] 上满足以下两个条件:(i) 在 [a, b] 上连续;(ii) 在 (a, b) 上可导,那么存在至少一个 c ∈ (a, b),使得
f'(c) = (f(b) - f(a))/(b - a)。 -
柯西中值定理:设函数 f(x) 和 g(x) 在闭区间 [a, b] 上满足以下两个条件:(i) 在 [a, b] 上连续;(ii) 在 (a, b) 上可导且 g’(x) ≠ 0,那么存在至少一个 c ∈ (a, b),使得
[f(b) - f(a)]/[g(b) - g(a)] = f'(c)/g'(c)。 -
泰勒定理:设函数 f(x) 在包含点 a 的开区间上有 n + 1 阶导数,则对于这个开区间内的任意 x,存在一个介于 x 和 a 之间的数 c,使得 f(x) 等于其在点 a 处以及其 (n + 1) 阶导数值的幂和的和,即
f(x) = f(a) + f'(a)(x - a) + f''(a)/2!(x - a)^2 + ... + f^(n)(a)/n!(x - a)^n + Rn(x)。
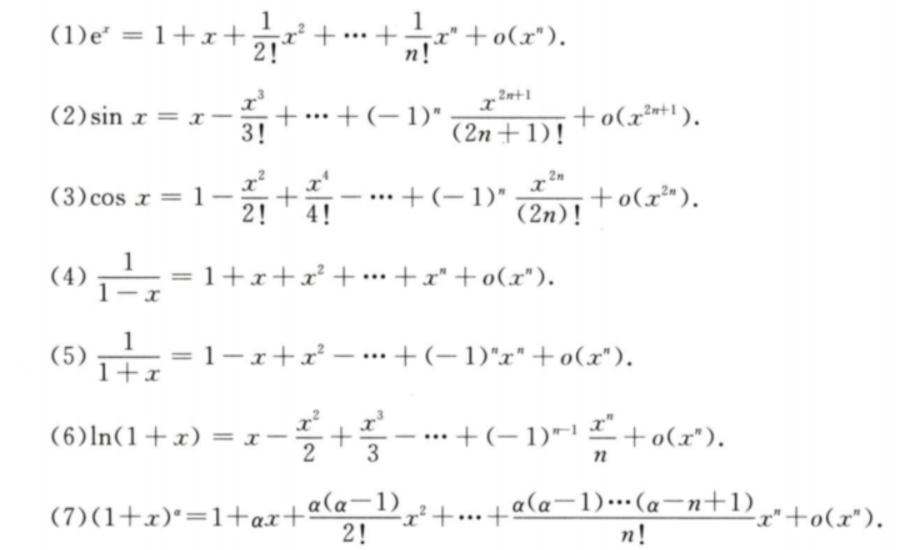
-
牛顿-莱布尼茨公式:假设函数 F(x) 是函数 f(x) 在闭区间 [a, b] 上的一个原函数(即 F’(x) = f(x)),那么函数 f(x) 在 [a, b] 上的定积分可以通过 F(x) 在 [a, b] 上的两个端点值之差来表示,即
∫[a,b]f(x)dx = F(b) - F(a)。 -
Stolz定理:假设 {an} 和 {bn} 分别是两个数列,满足 bn 严格递增,并且极限
lim(n→∞) an/bn = L(其中 L 可能为实数或 ±∞)。那么,对于每个 n 任何大于 n 都有lim(k→∞) ak/bk = L。 -
加强的积分中值定理:设函数 f(x) 和 g(x) 在闭区间 [a, b] 上连续,且 g(x) 不等于零。如果存在常数 K,使得
|∫[a,b]f(x)g(x)dx| ≤ K∫[a,b]|f(x)|dx成立,则存在至少一个 c ∈ (a, b),使得∫[a,b]f(x)g(x)dx = f(c)∫[a,b]g(x)dx。 -
二重积分中值定理:如果函数 f(x, y) 在闭矩形区域 D 上连续,且 g(x, y) 是 D 上的非负可测函数且不恒为零。那么存在至少一个点 (c, d) ∈ D,使得
∬D f(x, y)g(x, y) dA = f(c, d) ∬D g(x, y) dA,其中 dA 表示二重积分的元素面积。
这些定理在数学分析和积分学中起到重要的作用,可以帮助我们理解函数的特性、证明存在性、计算极限等。