视频作者：菜菜TsaiTsai
链接：【技术干货】菜菜的机器学习sklearn【全85集】Python进阶_哔哩哔哩_bilibili

白板推导里有写过程，但是当时理解的不太好，$\psi (x_i,\omega )$的理解有点问题也就是下面的$y_{\theta }(x_i)$

我们基于极大似然法来推导二元逻辑回归的损失函数，这个推导过程能够帮助我们了解损失函数怎么得来的，以及为什么$J(\theta )$的最小化能够实现模型在训练集上的拟合最好。

请时刻记得我们的目标：让模型对训练数据的效果好，追求损失最小。

关键概念：损失函数

衡量参数$\theta$的优劣的评估指标，用来求解最优参数的工具
损失函数小，模型在训练集上表现优异，拟合充分，参数优秀
损失函数大，模型在训练集上表现差劲，拟合不足，参数糟糕
我们追求，能够让损失函数最小化的参数组合

注意：没有”求解参数“需求的模型没有损失函数，比如KNN，决策树

二元逻辑回归的标签服从伯努利分布(即0-1分布)，因此我们可以将一个特征向量为$x$，参数为$\theta$的模型的一个样本$i$的预测情况表现为如下形式：
样本$i$在由特征向量$x_i$和参数$\theta$组成的预测函数中，样本标签被预测为1的概率为
$$P_1=P(\widehat{y_i}=1|x_i,\theta )=y_{\theta }(x_i)$$
样本$i$在由特征向量$x_i$和参数$\theta$组成的预测函数中，样本标签被预测为0的概率为
$$P_1=P(\widehat{y_i}=0|x_i,\theta )=1-y_{\theta }(x_i)$$
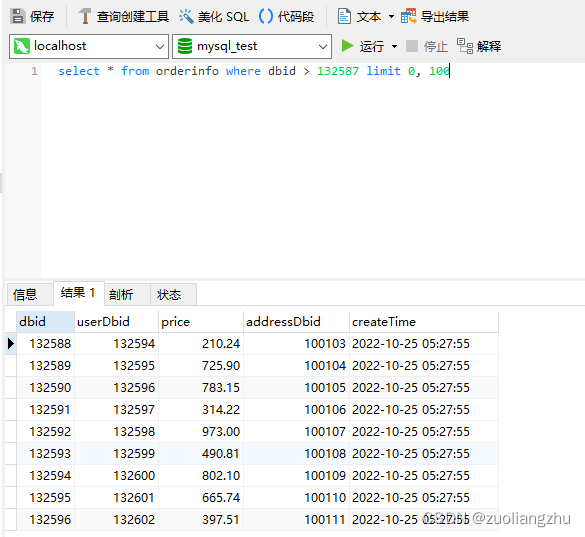
预测值与真实值之间的关系以及信息损失的关系如下图

将两种取值的概率整合，我们可以定义如下等式：
$$P(\widehat{y_i}|x_i,\theta )=P_1^{y_i}\cdot P_0^{1-y_i}$$

这个等式同时代表了$P_1$和$P_0$。
当样本$i$的真实标签$y_i$为1的时候，$1-y_i$就等于0，$P_0$的0次方就是1，所以$P(\widehat{y_i}|x_i,\theta )$就等于$P_1$，这个时候，如果$P_1$为1，模型的效果就最好，损失最小。
同理，当$y_i$为0的时候，$P(\widehat{y_i}|x_i,\theta )$就等于$P_0$，此时如果$P_0$非常接近1，模型的效果就很好，损失就很小。

为了达成让模型拟合好，损失小的目的，我希望任何取值下$P(\widehat{y_i}|x_i,\theta )$的值等于1。
而$P(\widehat{y_i}|x_i,\theta )$的本质是样本$i$由特征向量$x_i$和参数$\theta$组成的预测函数中，预测处所有可能的$\widehat{y_i}$的概率，因此1是它的最大值。也就是说，每时每刻，我们都在追求$P(\widehat{y_i}|x_i,\theta )$的最大值，这就将模型拟合中的“最小化损失”问题，转化成函数求解极值的问题

$P(\widehat{y_i}|x_i,\theta )$是对单个样本$i$而言的函数，对一个训练集的$n$个样本来说，我们可以定义如下等式来表达所有样本在特征矩阵$X$和参数$\theta$组成的预测函数中，预测处所有可能的$\hat{y}$的概率$P$为
$$\begin{array}{rl}P& =\prod _{i=1}^{n}P(\widehat{y_i}|x_i,\theta )\\ & =\prod _{i=1}^n(P_1^{y_i}\cdot P_0^{1-y_i})\\ & =\prod _{i=1}^n(y_{\theta }(x_i{)}^{y_i}\cdot (1-y_{\theta }(x_i){)}^{1-y_i})\end{array}$$
两侧同时取对数
$$\begin{array}{rl}\log P& =\log \prod _{i=1}^n(y_{\theta }(x_i{)}^{y_i}\cdot (1-y_{\theta }(x_i){)}^{1-y_i})\\ & =\sum _{i=1}^n\log (y_{\theta }(x_i{)}^{y_i}\cdot (1-y_{\theta }(x_i){)}^{1-y_i})\\ & =\sum _{i=1}^n(y_i\cdot \log y_{\theta }(x_i)+(1-y_i)\cdot \log (1-y_{\theta }(x_i)))\end{array}$$
这就是我们的交叉熵函数。为了数学上的便利以及更好地定义”损失”的含义，我们希望将极大值问题转换为极小值问题，因此我们对$\log P$取负，并且让参数$\theta$作为函数的自变量，就得到了损失函数$J(\theta )$
$$J(\theta )=-\sum _{i=1}^n(y_i\cdot \log y_{\theta }(x_i)+(1-y_i)\cdot \log (1-y_{\theta }(x_i)))$$
这就是一个，基于逻辑回归的返回值$y_{\theta }(x_i)$的概率性质得出的损失函数。在这个函数上，我们只要追求最小值，就能让模型在训练数据上的拟合效果最好，损失最低。
其中$\theta$表示求解出来的一组参数，$n$是样本个数，$y_i$是样本$i$上的真实标签，$y_{\theta }(x_i)$是样本$i$上基于参数$\theta$计算出来的逻辑回归返回值，$x_i$是样本$i$各个特征的取值
注意，在逻辑回归的本质函数$y(x)$例，特征矩阵$x$是自变量，参数㐊$\theta$。但在损失函数中，参数$\theta$是损失函数的自变量，$x$和$y$都是已知的特征矩阵和标签，相当于是损失函数的参数。

不同的函数中，自变量和参数各有不同，因此大家需要在数学计算中，尤其是求导的时候避免混淆。

关键概念：似然与概率

以样本$i$为例，我们有表达式
$$P(\widehat{y_i}|x_i,\theta )$$
对于这个表达式而言，如果参数$\theta$是一致的，特征向量$x_i$是未知的，我们便称$P$是在探索不同特征取值下获取所有可能的$\hat{y}$的可能性，这种可能性就被称为概率，研究的是自变量和因变量之间的关系
如果特征向量$x_i$是已知的，参数$\theta$是未知的，我们便称$P$是探索不同参数下获取所有可能的$\hat{y}$的可能性，这种可能性就被称作似然，研究的是参数取值与因变量之间的关系
在逻辑回归的建模过程中，我们的特征矩阵是已知的，参数是未知的，因此我们讨论的所有“概率”其实严格来说都是“似然”，所以逻辑回归的损失函数推导方法叫做“极大似然法”。也因此，一下式子又被称为“极大似然函数”
$$P(\widehat{y_i}|x_i,\theta )=y_{\theta }(x_i{)}^{y_i}\cdot (1-y_{\theta }(x_i){)}^{1-y_i}$$