👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
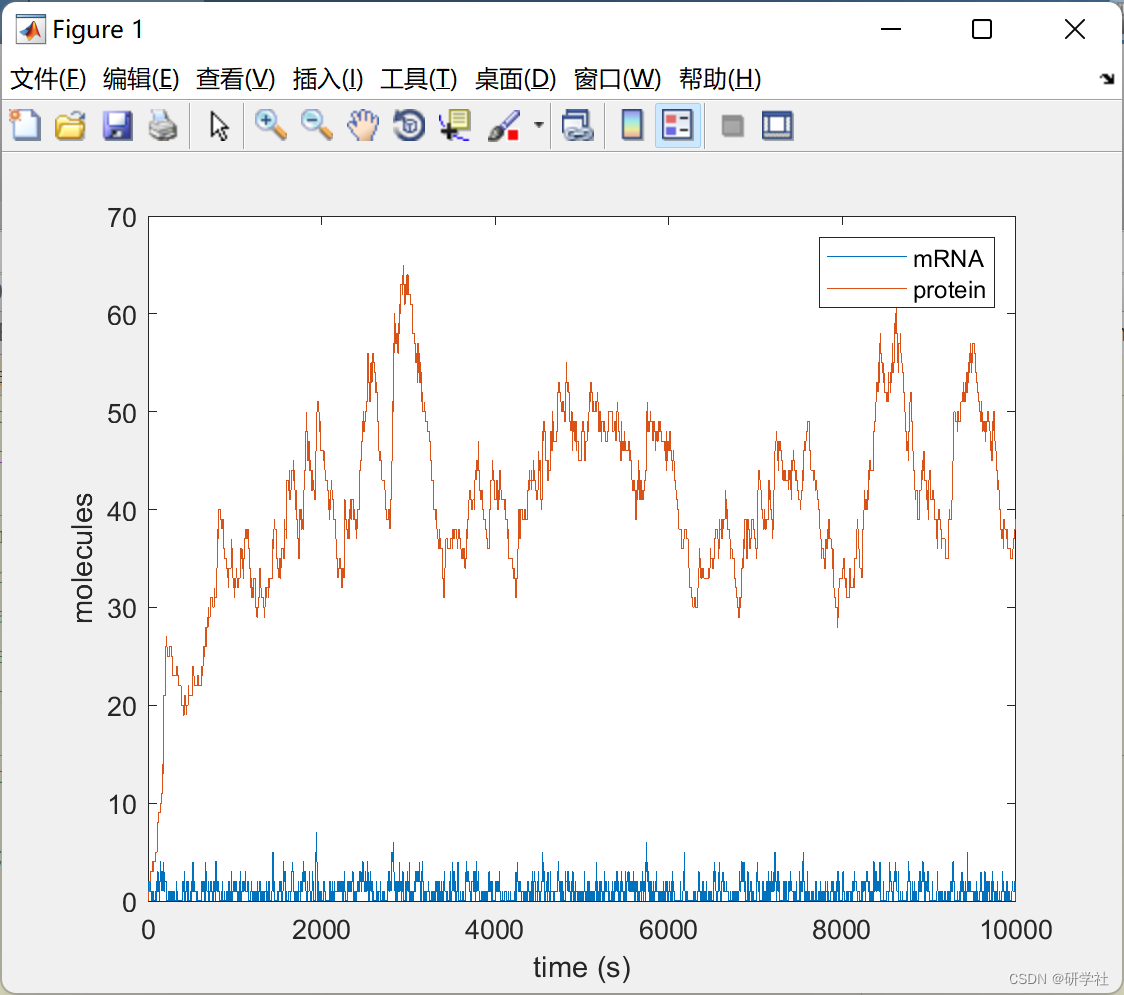
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
化学反应网络的动力学通常使用微分方程进行建模,将化学物质的数量视为连续和确定的量。如果反应分子的数量很少,随机分子波动就会变得显著,离散的随机建模方法通常更合适。在“良好混合”环境的假设下,这样的系统可以建模为连续时间马尔可夫过程,其概率分布遵循所谓的化学“主方程”。Gillespie 算法(或 SSA)是一种离散事件模拟算法,可生成随机过程的单一实现,这些实现与主方程具有精确的统计一致性。
📚2 运行结果
部分代码:
%% Reaction network:
% 1. transcription: 0 --kR--> mRNA
% 2. translation: mRNA --kP--> mRNA + protein
% 3. mRNA decay: mRNA --gR--> 0
% 4. protein decay: protein --gP--> 0
%% Rate constants
p.kR = 0.1;%0.01;
p.kP = 0.1;%1;
p.gR = 0.1;
p.gP = 0.002;
%% Initial state
tspan = [0, 10000]; %seconds
x0 = [0, 0]; %mRNA, protein
%% Specify reaction network
pfun = @propensities_2state;
stoich_matrix = [ 1 0 %transcription
0 1 %translation
-1 0 %mRNA decay
0 -1 ]; %protein decay
%% Run simulation
[t,x] = directMethod(stoich_matrix, pfun, tspan, x0, p);
%[t,x] = firstReactionMethod(stoich_matrix, pfun, tspan, x0, p);
%% Plot time course
figure();
stairs(t,x); set(gca,'XLim',tspan);
xlabel('time (s)');
ylabel('molecules');
legend({'mRNA','protein'});
end
function a = propensities_2state(x, p)
% Return reaction propensities given current state x
mRNA = x(1);
protein = x(2);
a = [p.kR; %transcription
p.kP*mRNA; %translation
p.gR*mRNA; %mRNA decay
p.gP*protein]; %protein decay
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Nezar (2022). Gillespie Stochastic Simulation Algorithm