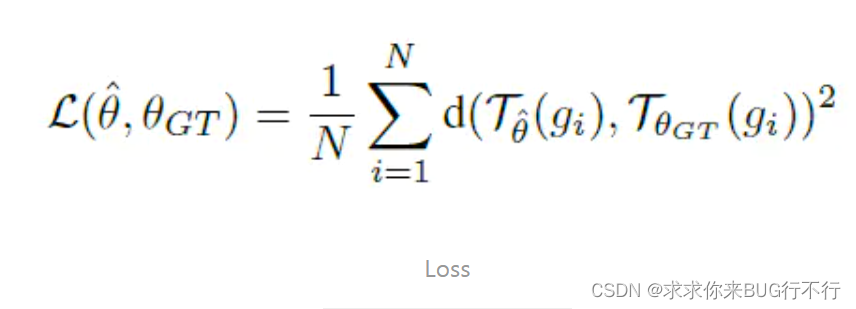参考视频：2.线性模型_哔哩哔哩_bilibili

参考视频中实现$$y=wx$$ 的代码，在加上偏置b后实现 $$y=wx+b$$ 的线性模型

假设我们有这样一个线性模型：$$y=wx+b$$

X和Y对应的数据如下

X	Y
1.0	5.0
2.0	8.0
3.0	11.0
4.0	？

预测值：$$\hat{y}=wx+b$$

误差Train Loss：$$loss=(\hat{y}-y{)}^2=(x\ast w-y{)}^2$$

平均平方误差MSE：$$cost=\frac{1}{N}\sum _{n=1}^N({\hat{y}}_n-y_n{)}^2$$

1 穷举法

首先一种方法是穷举法，假设w的范围是[0.0, 6.0]，b的范围也是[0.0,6.0]

穷举w和b的每一种组合，并计算每一次的误差，取误差最小的一次为最优解

下面是代码实现：

import numpy as np
import sys
from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [5.0, 8.0, 11.0]


def forward(x):
    return w * x + b


def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2


w_list = np.arange(0.0, 6.1, 0.1)
b_list = np.arange(0.0, 6.1, 0.1)
mse_list = []  # 平均平方误差

min_mse = sys.float_info.max  # 记录最小的MSE
best_w = -1.0  # 记录MSE最小时的w
best_b = -1.0  # 记录MSE最小时的b

for w in w_list:
    for b in b_list:
        l_sum = 0
        for x_val, y_val in zip(x_data, y_data):  # 以元组的形式遍历(x,y)
            loss_val = loss(x_val, y_val)  # 计算Loss
            l_sum += loss_val

        mse = l_sum / len(x_data)  # 计算这一次的MSE
        if mse < min_mse:
            min_mse = mse
            best_b = b
            best_w = w
        mse_list.append(mse)

print(str(best_w) + " " + str(best_b))

ax = plt.axes(projection='3d')
ax.set_xlabel('w', fontsize=14)
ax.set_ylabel('b', fontsize=14)
ax.set_zlabel(' Loss', fontsize=14)
X, Y = np.meshgrid(w_list, b_list)
Z = np.array(mse_list)

ax.scatter3D(X, Y, Z, c=Z, cmap='viridis')
plt.show()

用matplotlib画出三维图形，X轴是权重w，Y轴是偏置b，Z轴是Loss：

显然在w=3，b=2时Loss最小