目录

       归并排序递归实现

思想

图解

代码

归并排序的非递归版本

基本思想：

代码

---

归并排序递归实现

 思想

最主要的相当于二叉树遍历中的后序遍历。

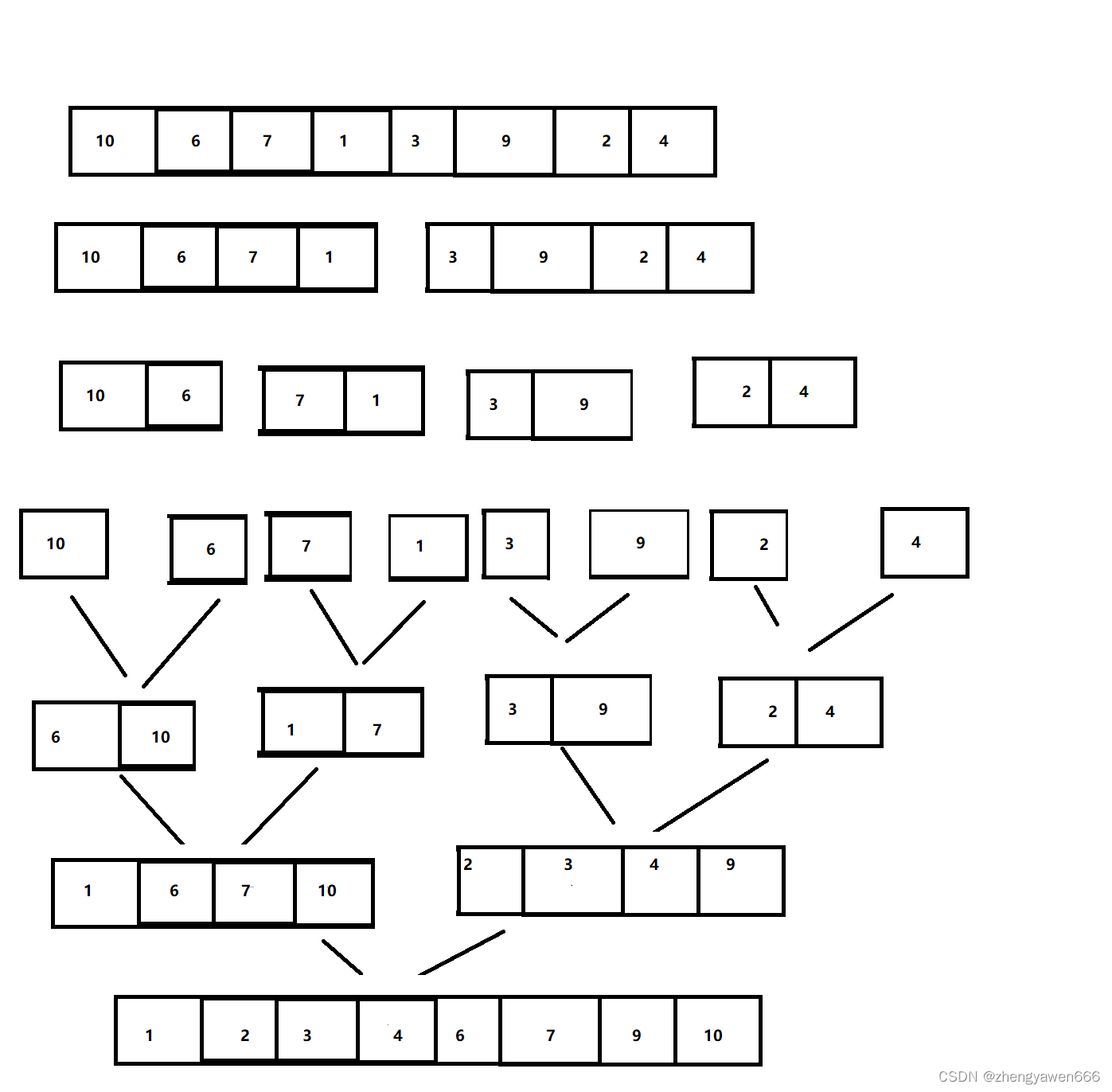
①将数组分割成多个小区间（当只有一个元素或者并不存在的时候就不用再分割了）

②对每一个小区间中的元素进行比较，从小到大排好之后，再返回给上一层；这一层排好之后再返回给这一层的上一层，直到排好整个区间内的元素。先分割左边的区间，再分割右边的区间，再对左区间进行排序，排好之后再排序右区间，最后合在一起。

需要借助一个额外的数组tmp，这一层递归的有序的结果是需要返回给上一层的。最后将排好序的tmp拷贝回a中

进行拷贝的条件是两个区间都存在，即有数据，如果不满足条件跳出循环，有可能其中一个还有数据没有拷贝完成，就要将剩下的数据全部都拷贝回数组

图解

  代码

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	assert(a && tmp);
	while (begin >= end)
	{
		return;
	}//

	int mid = (begin + end) / 2;
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);//分

	int begin1 = begin;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = end;
	int i = begin1;

	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}

	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

void MergeSort(int* a, int n)
{
	assert(a);
	int* tmp = (int*)malloc(sizeof(n));
	if (tmp == NULL)
	{
		printf("malloc fail!\n");
		exit(-1);
	}

	_MergeSort(a, 0, n - 1, tmp);

}

归并排序的非递归版本

基本思想：

递归排序的非递归版本由于是后序遍历，用栈和队列不太适合（比较适合前中序遍历）。

写成非递归版本主要是控制相应的区间的取值。我们可以手动进行控制，和刚才归并排序的思路差不多，相当于所有的都分成单个的区间，排好之后再返回给上一层排序，以此类推，知道排完

这里注意边界条件的控制

1 gap一开始的时候是1，这样子可以保证将数组分割成一个一个数字的小区间

2 循环的条件是gap<n，因为当gap等于n的时候是最后一层递归，相当于gap等于整个数组。

3 i+=2*gap的原因是一次归并的相当于两个数据，（大小区间都可以看做是一个数据。从宏观上来讲）

4 特别要注意边界条件的判断 如果只是单纯的这样写，不加边界条件的判断，那么很有可能会越界，只适合2^n的个数的数组

越界除了begin1都有可能越界

①如果end1和begin2越界了，那么就说明后面的一段区间是不存在的，我们可以不用判断这一个区间了（其他区间都是已经排好序的）

②如果是end2越界了，那么就需要修正end2的值，修正成数组的大小

注意这样子的话我们是需要每一次都将原数组的数据拷贝回a数组的，因为如果不判断就去递归的话，相当于这个数据不会返还给a了，那么对应的这里的位置就是随机值了。每递归一次返回一次是为了避免出现随机值

由于图和刚开始的差不多，就不画了

代码

void MergeSortNonR(int* a, int n)
{
	assert(a);
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc");
		exit(-1);
	}

	int gap = 1;
	while (gap < n)
	{
		int index = 0; 
		for (int i = 0; i < n; i += 2 * gap)
		{	
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			if (end1 >= n || begin2 >= n)
			{
				break;
			}
		
			if (end2 >= n)
			{
				end2 = n - 1;
			}

			//归并
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}


		}
		for (int j = 0; j < index; j++)
		{
			a[j] = tmp[j];
		}
		gap *= 2;
	}

	free(tmp);
	tmp = NULL;
}