【HDU No. 3567】八数码 II Eight II

杭电OJ 题目地址

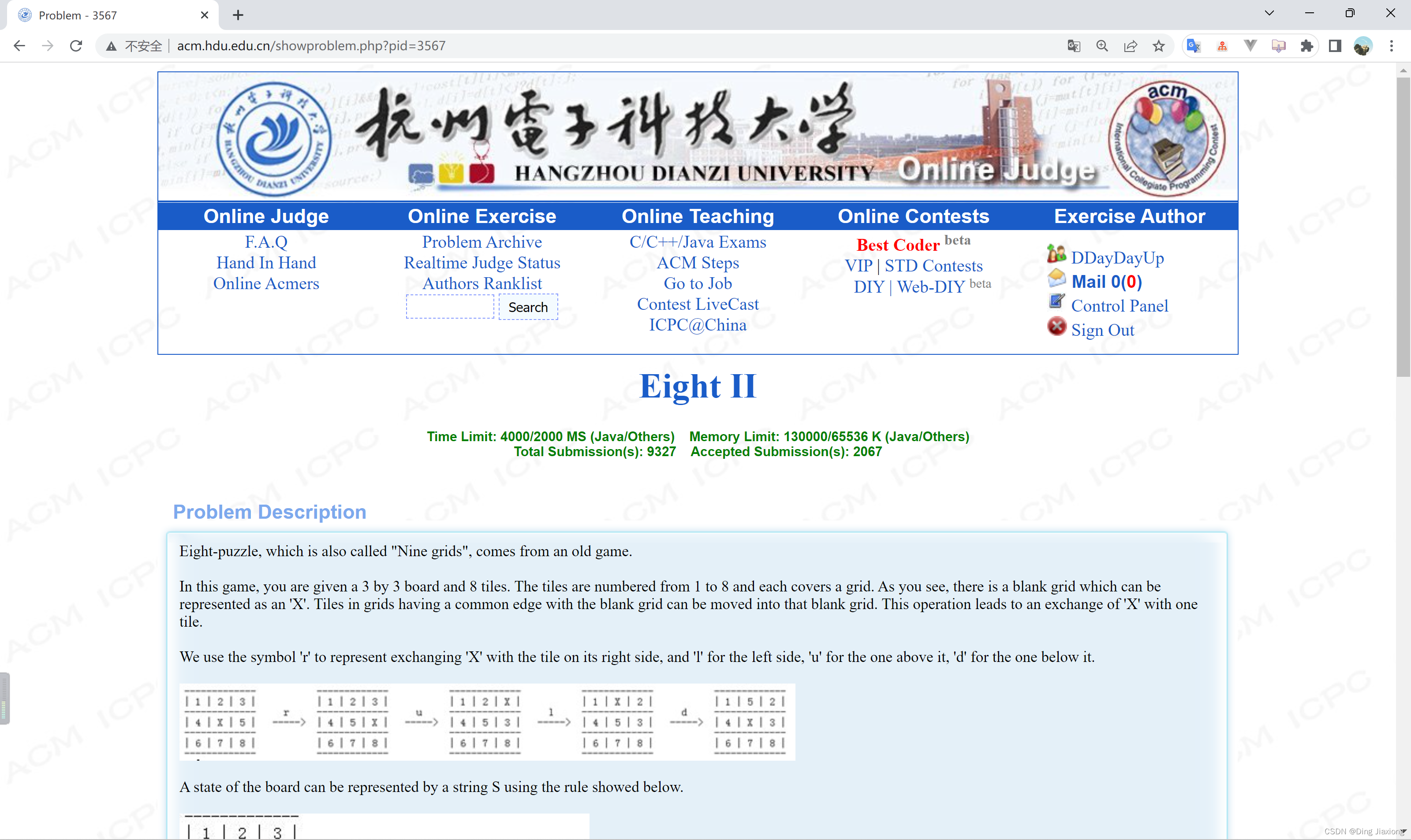
【题意】

八数码，也叫作“九宫格”，来自一个古老的游戏。在这个游戏中，你将得到一个3×3的棋盘和8个方块。方块的编号为1～8，其中一块方块丢失，称之为“X”。“X”可与相邻的方块交换位置。用符号“r”表示将“X”与其右侧的方块进行交换，用“l”表示左侧的方块，用“u”表示其上方的方块，用“d”表示其下方的方块。

棋盘的状态可以用字符串S表示，使用下面显示的规则。

问题是使用“r”“u”“l”“d”操作列表可以将棋盘的状态从状态A转到状态B，需要找到满足以下约束的结果：

1. 在所有可能的解决方案中，它的长度最小；
2. 它是所有最小长度解中词典序最小的一个。

【输入输出】

输入：

第1行是T （T ≤200），表示测试用例数。每个测试用例的输入都由两行组成，状态A位于第1行，状态B位于第2行。保证从状态A到状态B都有有效的解决方案。

输出：

对于每个测试用例，都输出两行。第1行是“Case x :d”格式，其中x 是从1开始计算的案例号，d 是将A转换到B的操作列表的最小长度。第2行是满足约束条件的操作列表。

【思路分析】

本题为八数码问题，与前面八数码问题（HDU1043）不同的是，本题的终态（目标状态）不是固定不变的，而是由输入确定的。要求从初A到终态B，输出最少的步数和操作序列，而且如果最小步数相同，则输出字典序最小的一个。本题保证有解，无须可解性判断，可以采用A*、IDA算法解决，在此采用IDA算法。

【算法设计】

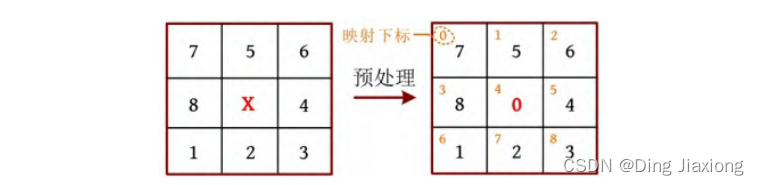
[1] 读入初态，用变量x 记录“X”出现的位置i ，令a [i ]=0，将其他位置减去“0”转换成数字。例如，初态为564178X23，用变量x记录“X”出现的位置6，转换之后的棋盘如下图所示。

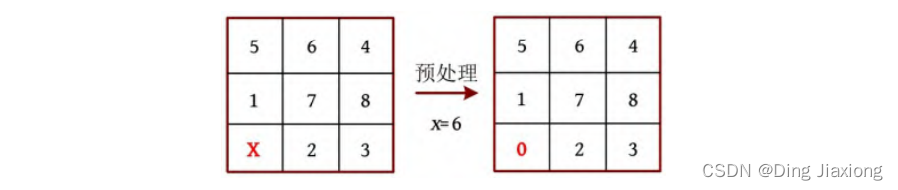
[2] 读入终态，“X”出现的位置为i ，令goal[i ]=0，其他位置减去“0”转换成数字。上题（HDU1043）中目标状态数字正好等于位置下标，本题中的目标状态是根据输入数据确定的，为了方便计算启发函数，对目标状态建立一个从数字到位置下标的映射。将goal[i ]映射到位置下标i ，m [goal[i ]]=i 。

例如，终态为7568X4123，转换之后的棋盘如下图所示，m[7]=0，m [6]=2。

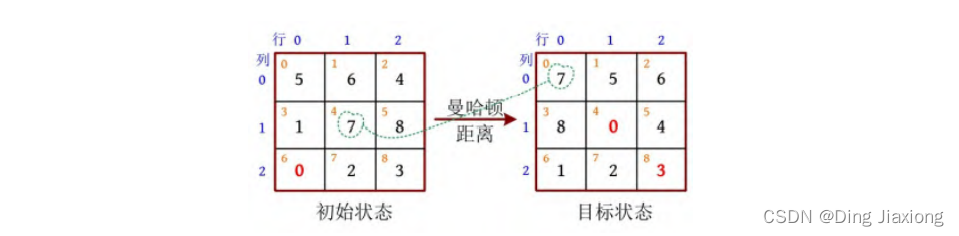
[3] 计算初态启发函数并初始化深度depth=h()。如下图所示，初始状态中数字7的位置下标为4，转换为4/3行、4%3列，即1行、1列。目标状态中数字7的映射位置下标为0，转换为0/3行、0%3列，即0行、0列。两个位置的曼哈顿距离为|1-0|+|1-0|=2。除了0（X滑块），计算当前状态和目标状态中每个位置的曼哈顿距离之和。

[4] 深度优先搜索，计算当前状态的启发函数h ()，如果正好为0，则找到目标输入答案，返回1。如果d +t >depth，则更新mindep=min(mindep, d +t )，返回0。

[5] 沿着4个方向搜索，如果x 的新位置未出边界、不是前一个位置，则交换原位置和新位置，记录操作序列，从新位置开始深度加1，进行深度优先搜索，如果找到答案，则返回1，否则交换原位置和新位置，还原现场并回溯。

[6] 如果未找到答案，则深度为depth=mindep，继续进行迭代加深搜索。

【算法实现】

定义方向数组及操作序列，操作序列字母按字典序排序。

#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
const int inf=0x3f3f3f3f;
const int dir[4][2]={{1,0},{0,-1},{0,1},{-1,0}};
const char str[]={'d','l','r','u'};//保证字母序
int a[9],goal[9],m[9];
int depth,mindep;
char ans[1000005];

int h(){//启发函数，曼哈顿距离（行列差绝对值之和） 
	int cost=0;
	for(int i=0;i<9;i++){
		if(a[i])
			cost+=abs(i/3-m[a[i]]/3)+abs(i%3-m[a[i]]%3);
	}
	return cost;
}

bool dfs(int x,int d,int pre){
	int t=h();
	if(!t){
		printf("%d\n",d);
		ans[d]='\0';
		printf("%s\n",ans);
		return 1;
	}
	if(d+t>depth){
		mindep=min(mindep,d+t);
		return 0;
	}
	for(int i=0;i<4;i++){
		int row=x/3+dir[i][0];
		int col=x%3+dir[i][1];
		int newx=row*3+col;//转换为数字 
		if(row<0||row>2||col<0||col>2||newx==pre) continue;
		swap(a[newx],a[x]);
		ans[d]=str[i];
		if(dfs(newx,d+1,x)) return 1;
		swap(a[newx],a[x]);
	}
	return 0;
}

void IDAstar(int x){
	depth=h();
	while(1){
		mindep=inf;
		if(dfs(x,0,-1))
			break;
		depth=mindep;
	}
}

int main(){
	int T,x,cas=0;
	scanf("%d",&T);
	while(T--){
		scanf("%s",ans);
		for(int i=0;i<9;i++){
			if(ans[i]=='X')//大写X
				x=i,a[i]=0;
			else
				a[i]=ans[i]-'0';
		}
		scanf("%s",ans);
		for(int i=0;i<9;i++){
			if(ans[i]=='X')
				goal[i]=0;
			else
				goal[i]=ans[i]-'0';
			m[goal[i]]=i;//映射位置
		}
		printf("Case %d: ",++cas);
		IDAstar(x);
	}
	return 0;
}