前缀和差分
- 一、前缀和
- 1、 什么是前缀和
- 2、 前缀和的作用
- 3、 前缀和的例题和模板
- (1)一维数组的前缀和
- C++版
- C版
- (2)二维数组的前缀和
- a.思路:
- b.题目和模板:
- C++版
- C版
- 二、差分
- 1、什么是差分?
- 2、差分有什么作用?
- 3、一维差分:
- (1)思路:
- (2)题目和模板
- C++版
- C版
- (3)优化
- C++版
- C版
- 4、二维差分:
- (1)思路:
- (2)题目和模板
- C++版
- C版
一、前缀和
1、 什么是前缀和
在解释什么是前缀和之前,我们先回顾一下高中学过的数列:
我们这里所说的前缀和其实就是我们在高中学的数列中的Sn(前n项和),只是我们这里需要将S1 , S2 , S3 , S4 …… Sn当作一个新的数组。
为了这个式子的高度统一性,我们的S0和a0都是不存储数据的,将其设置为0,这样当n等于1的时候,也满足上面的式子。
2、 前缀和的作用
我们看下面这段数学推导:

如果我们想特定几项an的和,那么我们就需要取遍历数组an,然后才能求出最终的和,我们发现这种情况的时间复杂度是O(N)。
但是我们使用前缀和Sn去计算的话,我们发现只需要一个简单是式子,其时间复杂度是O(1)。因此,我们便能够发掘出前缀和的作用:更快地求解数列的和
而这除了是利用了数学中的数列知识,更是一种用空间换时间的重要思想。
3、 前缀和的例题和模板
(1)一维数组的前缀和
其实前缀和就是一个公式,因此其模板是很简单的。
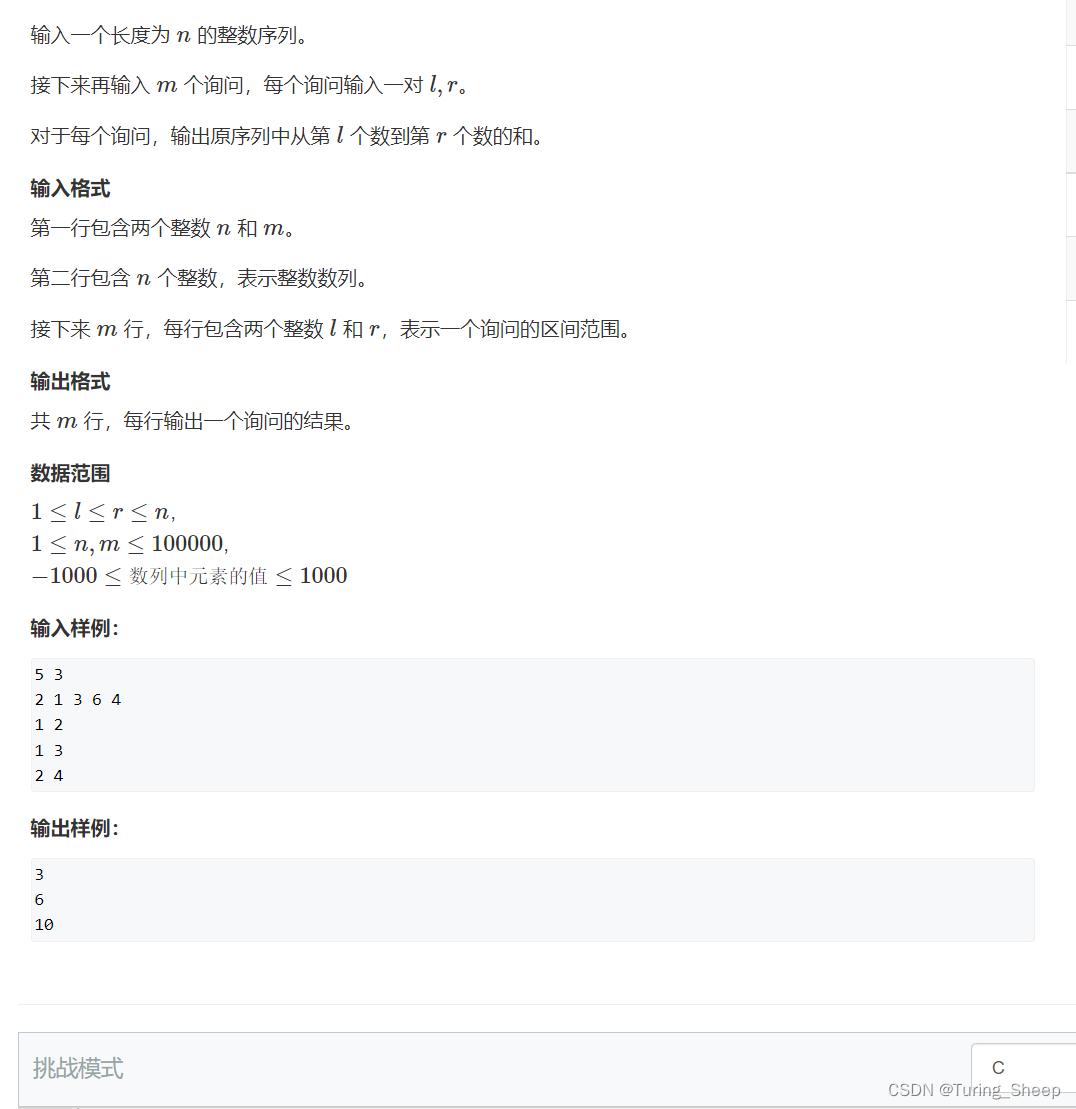
C++版
#include<iostream>
using namespace std;
const int N=1e6+10;
int arr[N];
int S[N];
int main()
{
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&arr[i]);
for(int i=1;i<=n;i++)S[i]=S[i-1]+arr[i];
while(m--)
{
int l,r;
scanf("%d %d",&l,&r);
printf("%d\n",S[r]-S[l-1]);
}
return 0;
}
C版
#include<stdio.h>
const int N=1e6+10;
int main()
{
int arr[N];
int S[N];
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&arr[i]);
for(int i=1;i<=n;i++)S[i]=S[i-1]+arr[i];
while(m--)
{
int l,r;
scanf("%d %d",&l,&r);
printf("%d\n",S[r]-S[l-1]);
}
return 0;
}
(2)二维数组的前缀和
a.思路:
在了解思路之前,我们应该先明白,什么是二维数组的前缀和,即二维数组的前n项和所指的是哪几项的和?
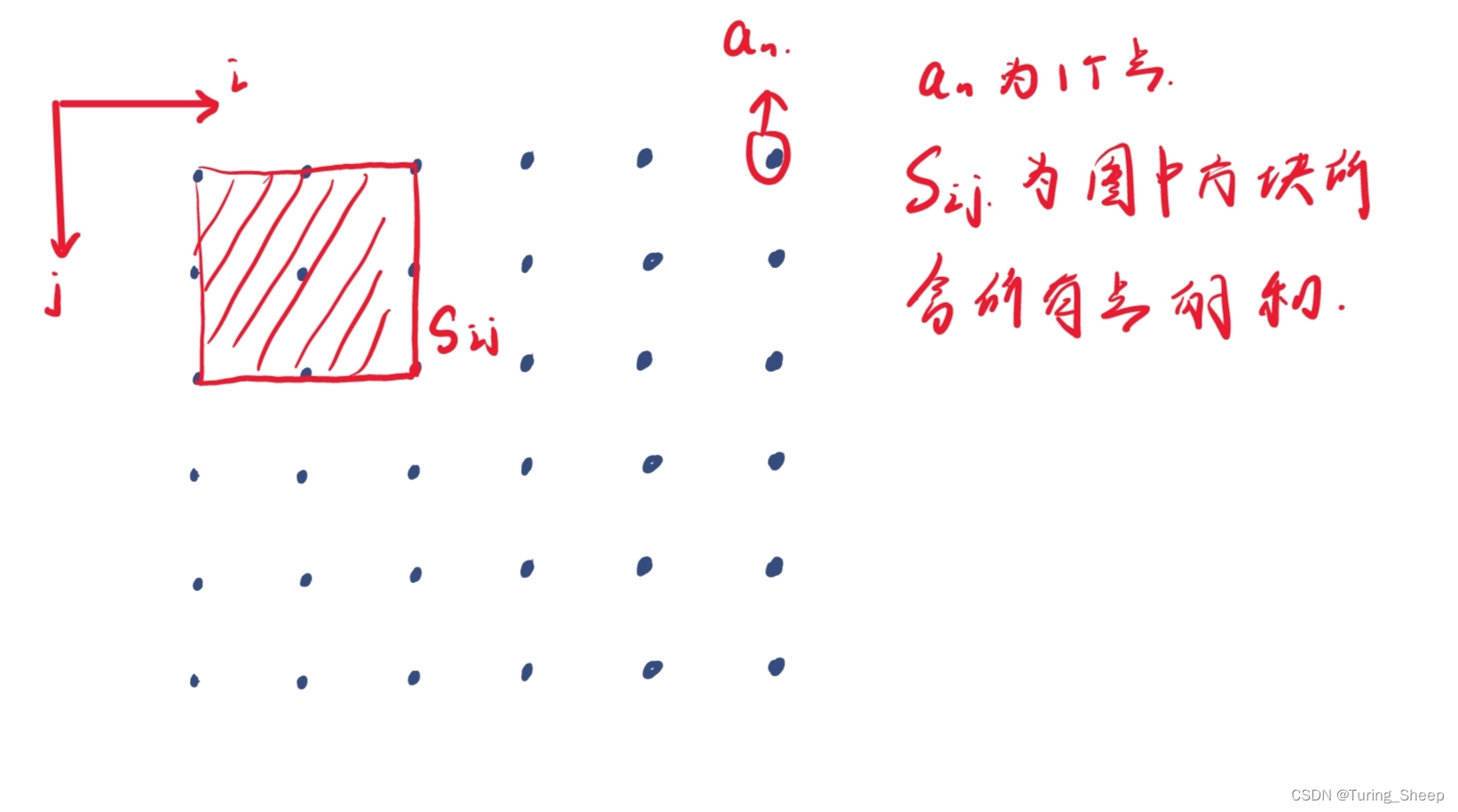
如图中所示,二维数组的前缀和就是图中方形所覆盖的an的和,包括边界!!!!
那么我们如何利用递推公式写出前缀和呢?
如下图所示:
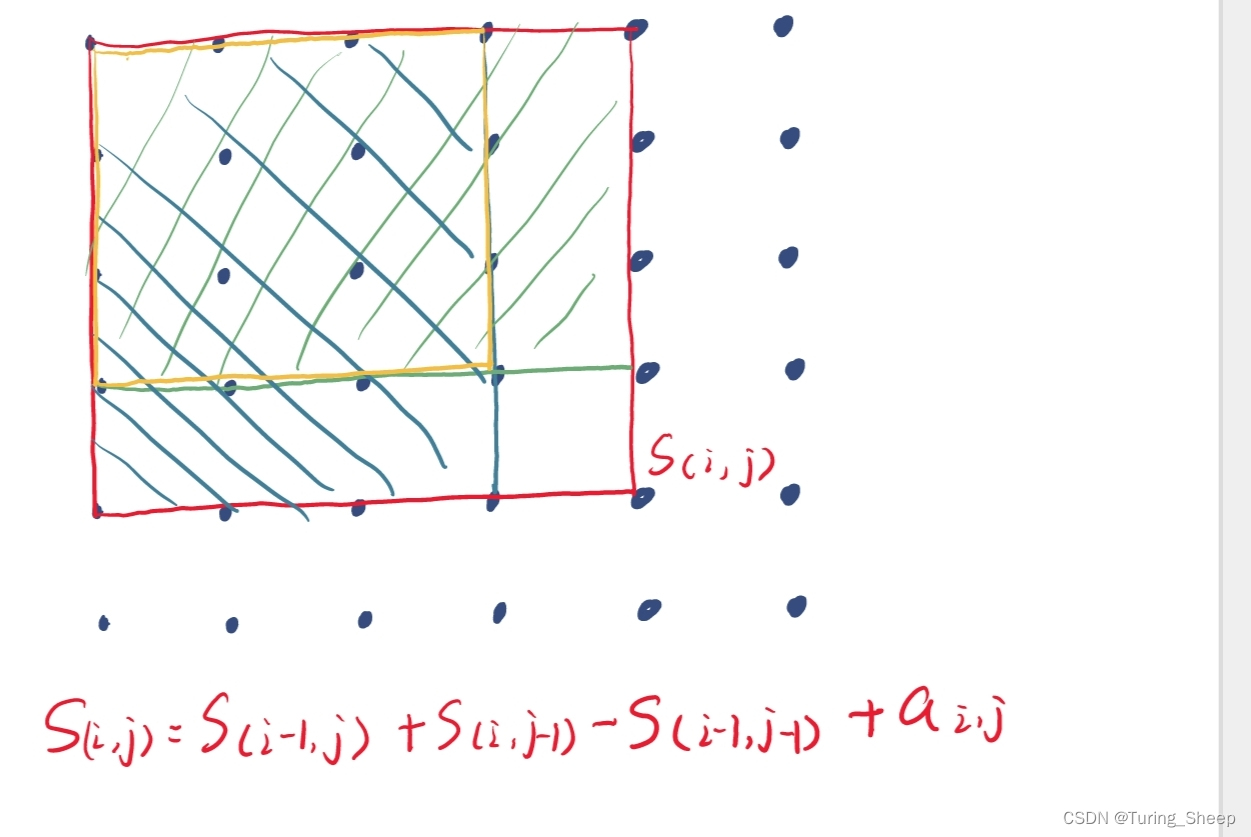
那么在理解了二维数组的前缀和的概念后,我们看下面这个问题:
我们如何计算这个紫色方形范围内的an的面积呢?
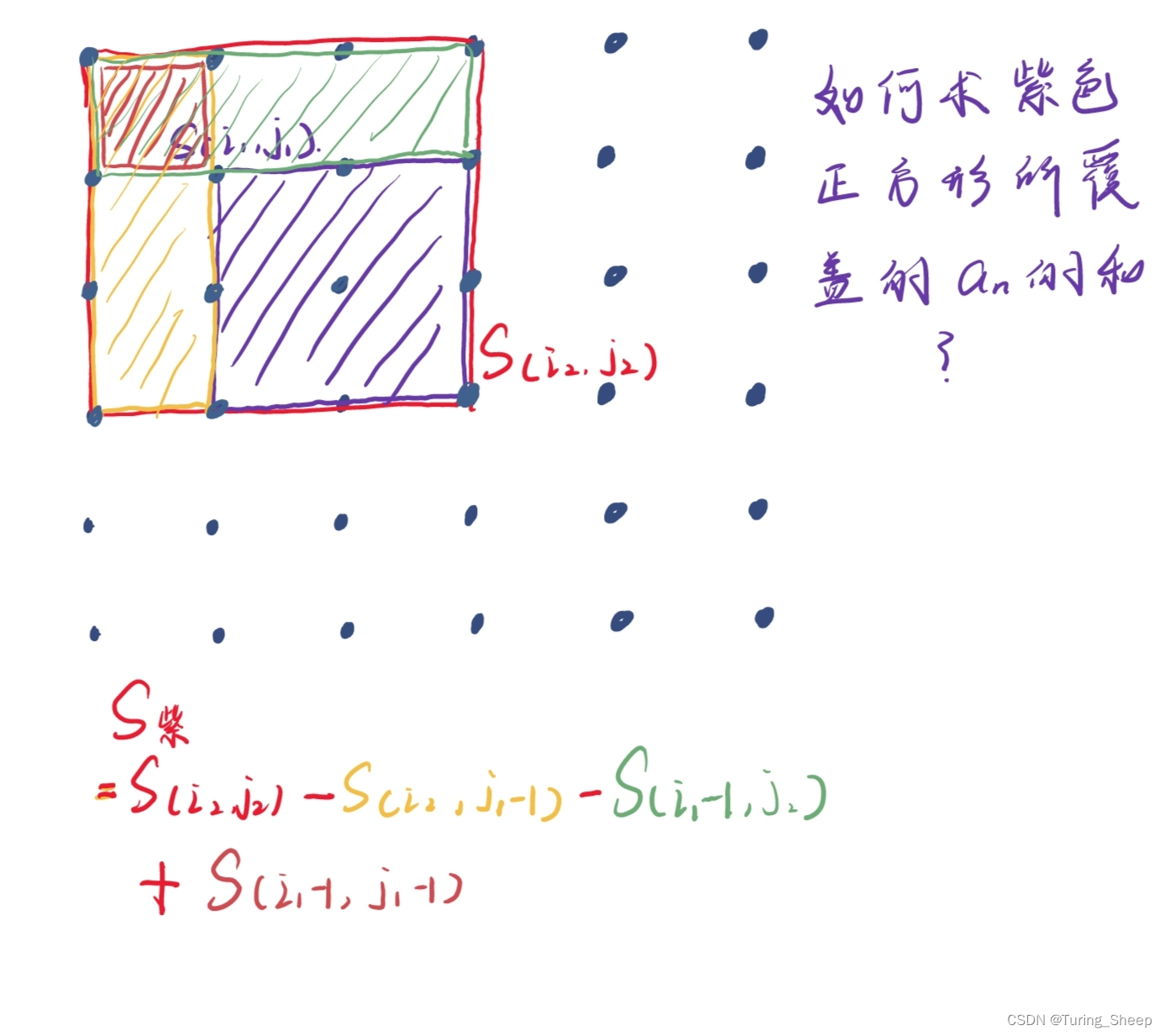
图中所示的求法类似于我们高中所学的概率内容中的容斥原理。
即我们先减去两部分,然后再加上重复减去的部分。但是我们要时刻注意边界问题,图中的式子之所以减一,就是因为紫色方形的边界也要算到前缀和中。
b.题目和模板:
题目:

C++版
#include<iostream>
using namespace std;
const int N=1010;
int a[N][N];
int S[N][N];
int main()
{
int n,m,q;
scanf("%d %d %d",&n,&m,&q);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
S[i][j]=S[i-1][j]+S[i][j-1]-S[i-1][j-1]+a[i][j];
}
}
while(q--)
{
int x1,y1,x2,y2;
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
printf("%d\n",S[x2][y2]-S[x2][y1-1]-S[x1-1][y2]+S[x1-1][y1-1]);
}
return 0;
}
C版
#include<stdio.h>
const int N=1010;
int main()
{
int a[N][N];
int S[N][N];
int n,m,q;
scanf("%d %d %d",&n,&m,&q);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
S[i][j]=S[i-1][j]+S[i][j-1]-S[i-1][j-1]+a[i][j];
}
}
while(q--)
{
int x1,y1,x2,y2;
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
printf("%d\n",S[x2][y2]-S[x2][y1-1]-S[x1-1][y2]+S[x1-1][y1-1]);
}
return 0;
}
二、差分
1、什么是差分?
我们知道前缀和是一个数组中的前N项和,其实差分就是原数组an。
因此我们就能够发现,一个数列当中,an是差分,an的前n项和sn是前缀和。
2、差分有什么作用?
我们通过前缀和可以在时间复杂度为O(1)的情况下,计算出几项的和。那么差分则可以在时间复杂度为O(1)的情况下,给数列中的某几项都加上常数C。假设我们不适用差分的话,我们需要遍历原数组然后逐一加上常数C,此时的时间复杂度就是O(N)。
由此我们就能够总结出差分的作用:在时间复杂度是O(1)的前提下,将数组中的某几项加上特定的常数C。那么怎么加呢?我们看下面的内容。
3、一维差分:
(1)思路:
我们应该如何实现上面所说的差分的作用呢?我们看下面这张图片:

由上图可知:
我们只需要将bn中的第L项加上C,第r+1项减去C即可。这样我们在通过bn算an的时候,就能够在L到r的闭区间上的an都加上常数C。但此时的时间复杂度仅仅是O(1)。
(2)题目和模板
C++版
#include<iostream>
using namespace std;
const int N=100001;
int a[N];
int b[N];
int main()
{
//读取数据
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",a+i);
//构造b数组:使得ai是bi的前缀和
for(int i=1;i<=n;i++)b[i]=a[i]-a[i-1];
while(m--)
{
//读取插入的区间和数据
int l,r,c;
scanf("%d %d %d",&l,&r,&c);
b[l]+=c;
b[r+1]-=c;
}
//利用b数组打印a数组
for(int i=1;i<=n;i++)printf("%d ",b[i]+=b[i-1]);
return 0;
}
C版
#include<stdio.h>
const int N=100001;
int main()
{
int a[N];
int b[N];
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",a+i);
for(int i=1;i<=n;i++)b[i]=a[i]-a[i-1];
while(m--)
{
int l,r,c;
scanf("%d %d %d",&l,&r,&c);
b[l]+=c;
b[r+1]-=c;
}
for(int i=1;i<=n;i++)printf("%d ",b[i]+=b[i-1]);
return 0;
}
(3)优化
这里我们在介绍一种不用特意构造b数组的方法。
我们假设an数列初始化全为0,那么此时我们输入a1的时候,就相当于在[1,1]上插入一个a1。同理,an就相当于在[n,n]上插入一个an。我们就能够采用这种方式来初始化bn数组,如果不理解的话,大家可以自己写几个例子。
C++版
#include<iostream>
using namespace std;
const int N=100010;
int a[N],b[N];
void insert(int l,int r,int c)
{
b[l]+=c;
b[r+1]-=c;
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
scanf("%d",a+i);
insert(i,i,a[i]);
}
while(m--)
{
int l,r,c;
scanf("%d %d %d",&l,&r,&c);
insert(l,r,c);
}
for(int i=1;i<=n;i++)printf("%d ",b[i]+=b[i-1]);
return 0;
}
C版
#include<stdio.h>
int a[100010],b[100010];
void insert(int l,int r,int c)
{
b[l]+=c;
b[r+1]-=c;
}
int main()
{
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",a+i);
insert(i,i,a[i]);
}
while(m--)
{
int l,r,c;
scanf("%d %d %d",&l,&r,&c);
insert(l,r,c);
}
for(int i=1;i<=n;i++)printf("%d ",b[i]+=b[i-1]);
return 0;
}
4、二维差分:
(1)思路:
我们先上下面的图示:
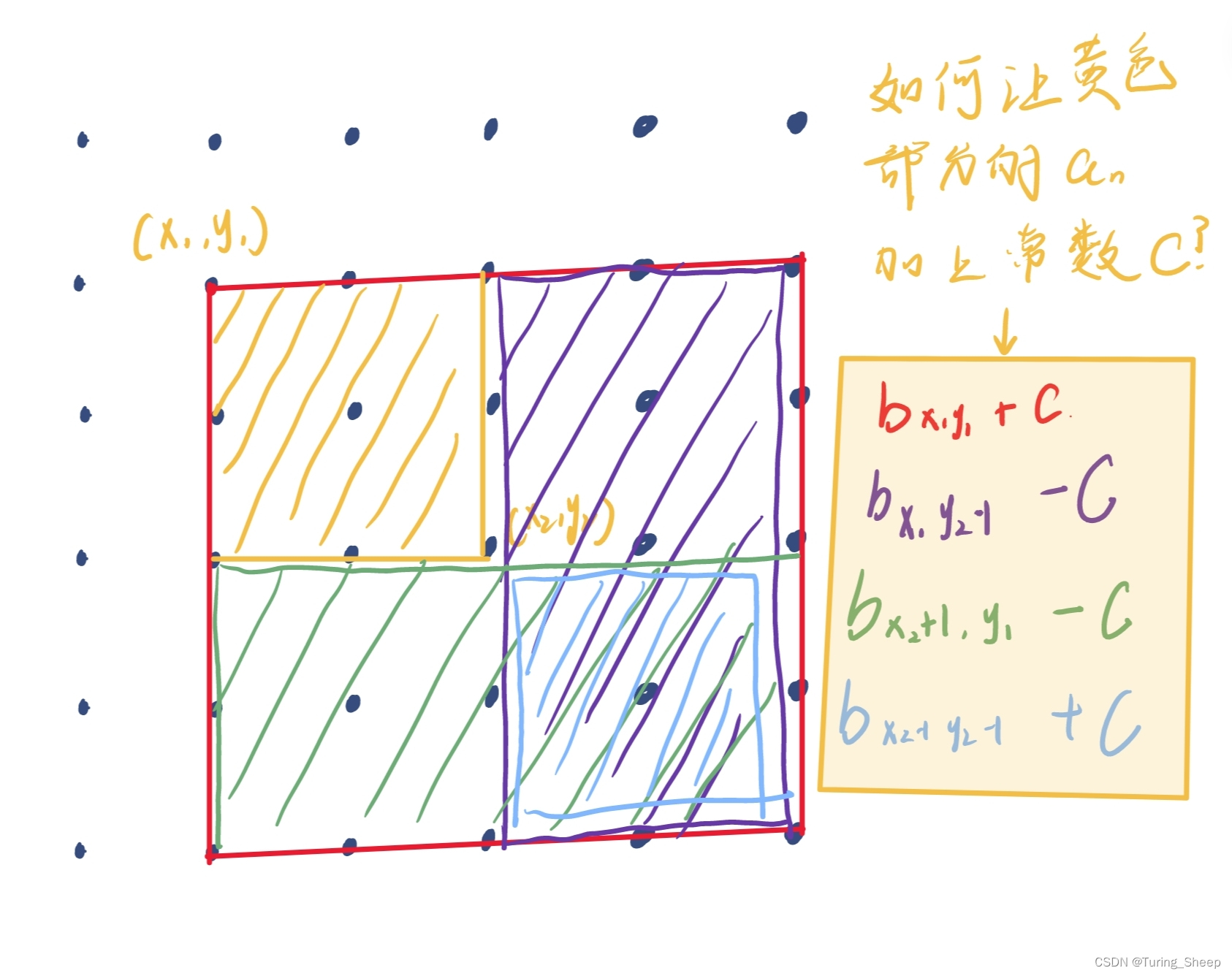
先解决第一个问题,为什么b[i,j]+c后是右下角的数列元素加c呢?其实很好理解,因为an是bn的前n项和,因此只有右下角的an计算时,才会包括该点。因此,b[i,j]+c后影响的是右下角。
然后我们就可以根据上图中公式使得黄色区域的an都加上C。
(2)题目和模板
C++版
#include<iostream>
using namespace std;
const int N=1010;
int a[N][N];
int b[N][N];
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1]+=c;
b[x2+1][y1]-=c;
b[x1][y2+1]-=c;
b[x2+1][y2+1]+=c;
}
int main()
{
int n,m,q;
cin>>n>>m>>q;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
insert(i,j,i,j,a[i][j]);
}
}
while(q--)
{
int x1,y1,x2,y2,c;
cin>>x1>>y1>>x2>>y2>>c;
insert(x1,y1,x2,y2,c);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
a[i][j]=a[i][j-1]+a[i-1][j]-a[i-1][j-1]+b[i][j];
printf("%d ",a[i][j]);
}
cout<<endl;
}
return 0;
}
C版
#include<stdio.h>
int a[1010][1010];
int b[1010][1010];
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1]+=c;
b[x2+1][y1]-=c;
b[x1][y2+1]-=c;
b[x2+1][y2+1]+=c;
}
int main()
{
int n,m,q;
scanf("%d %d %d",&n,&m,&q);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
insert(i,j,i,j,a[i][j]);
}
}
while(q--)
{
int x1,y1,x2,y2,c;
scanf("%d %d %d %d %d",&x1,&y1,&x2,&y2,&c);
insert(x1,y1,x2,y2,c);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
a[i][j]=a[i][j-1]+a[i-1][j]-a[i-1][j-1]+b[i][j];
printf("%d ",a[i][j]);
}
printf("\n");
}
return 0;
}


![[MySQL]数据库的约束与表的设计](https://img-blog.csdnimg.cn/abd5f229cb134f7bb9bafb4726753ac7.jpeg)