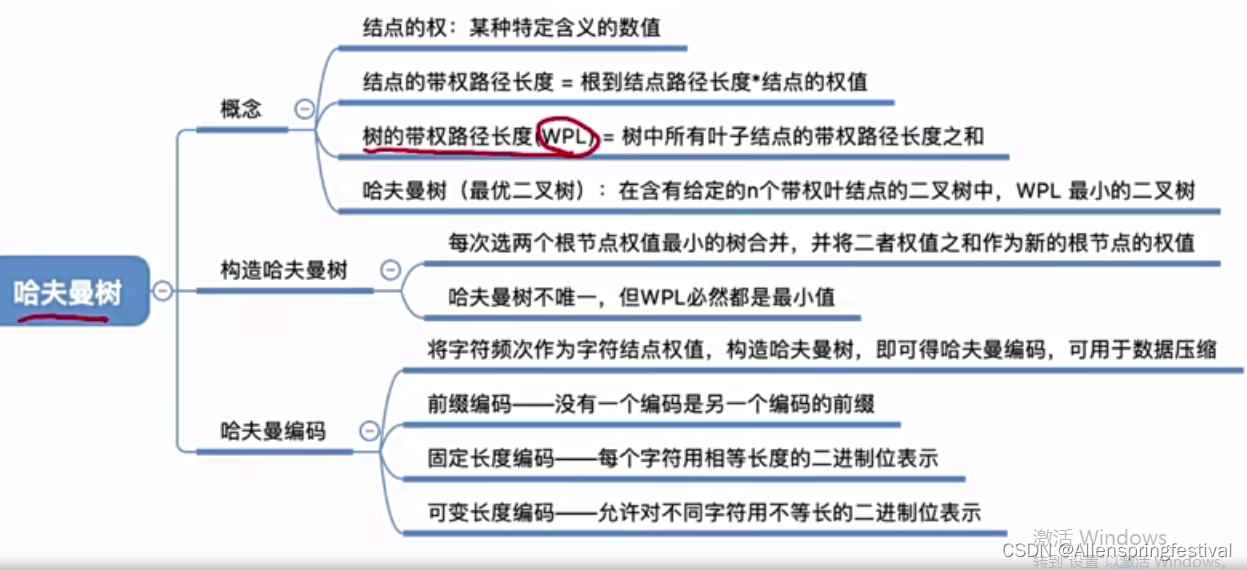
知识总览：

 概念：

结点的权：有某种现实含义的数值（如：表示结点的重要性）

结点的带权路径长度：从树的根到该结点的路径长度（经过的边数）与该结点上权值的乘积。

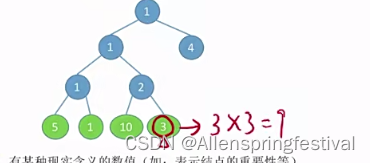
 就比如说要求画的这个结点的带权路径长度，从根节点到这个节点的路径长度为3，再乘以权值，那么带权路径长度为9。

树的带权路径长度：树中所有的叶节点的带权路径长度之和（WPL,WEIGHTED PATH LENGTH）

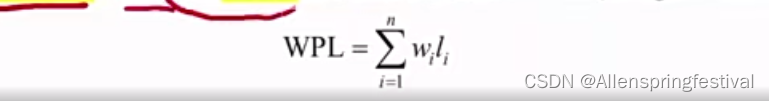
以下有实战例题：

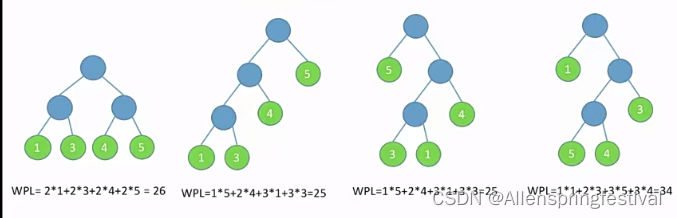
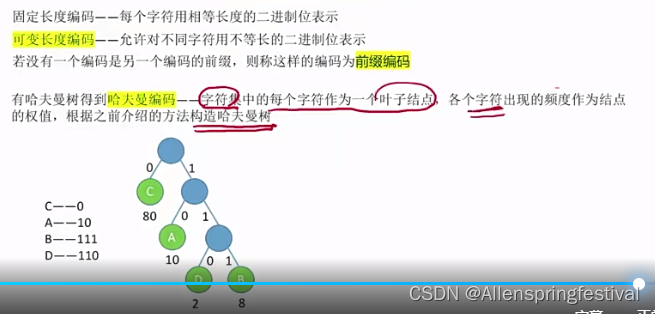
 在含有n个带权叶节点的二叉树中，其中带权路径长度(WPL)最小的二叉树称为哈夫曼树，也称作最优二叉树。

我们定义上述4个叶子结点的权值为1345，那我们定义不同的二叉树，其中WPL最小的。

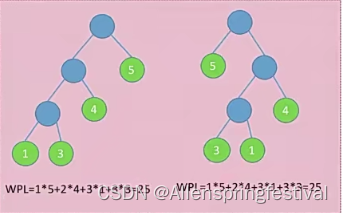
 这样我们发现中间这两棵树就是哈夫曼树。

哈夫曼树的构造：

 选择权值最小的两个节点结合变成兄弟：

 再从上述新生成的的4个结点中再次找两个最小的：

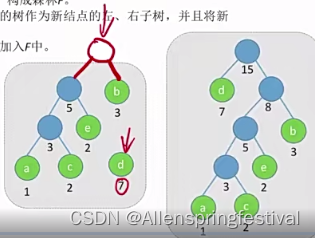
我们可以得到WPL最小的树：

2）哈夫曼树的结点总数为2n-1

3）哈夫曼树中不存在度为1的结点

4）哈夫曼树并不唯一，但WPL必然相同且为最优。

哈夫曼树的经典应用：

（1）（哈夫曼树编码）

（2）传递答案：

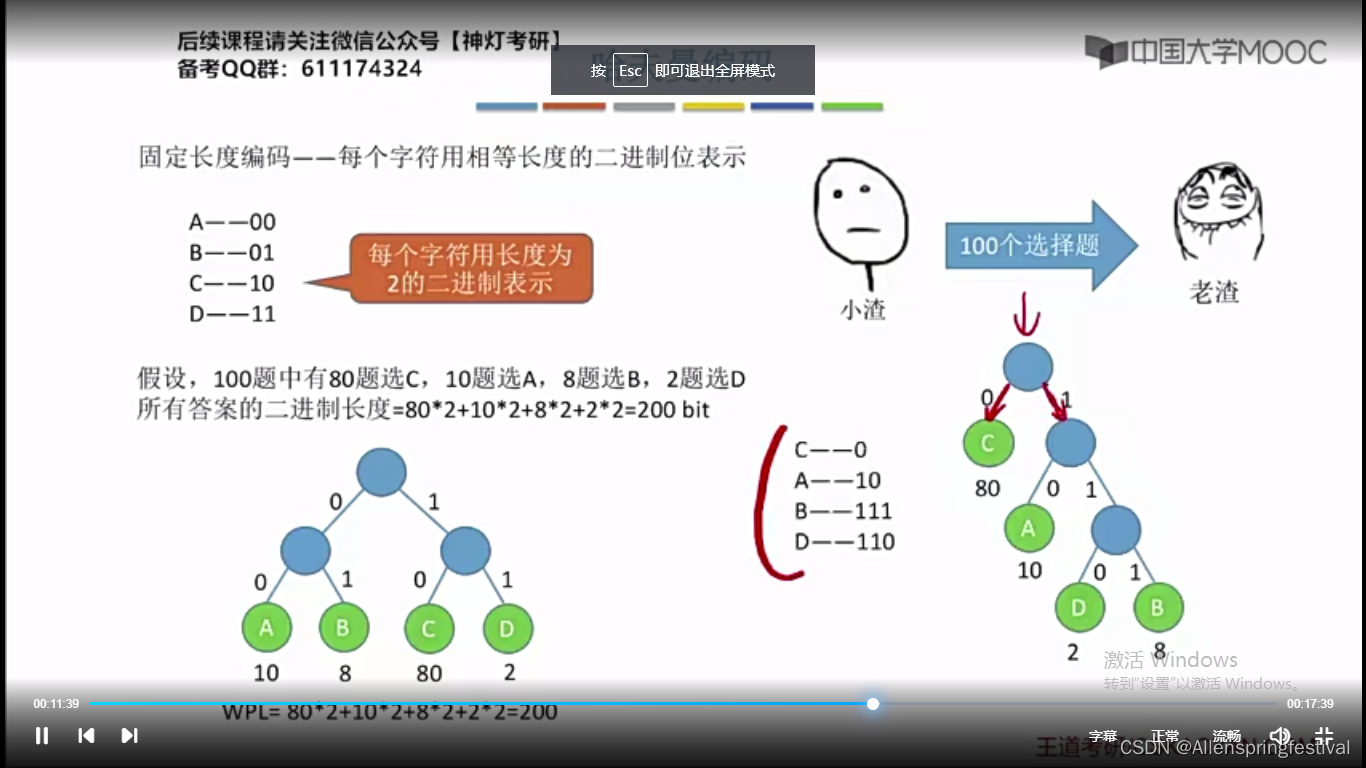
 这哥们需要咳嗽130次。

 用可变长度编码可能会导致解码错误。

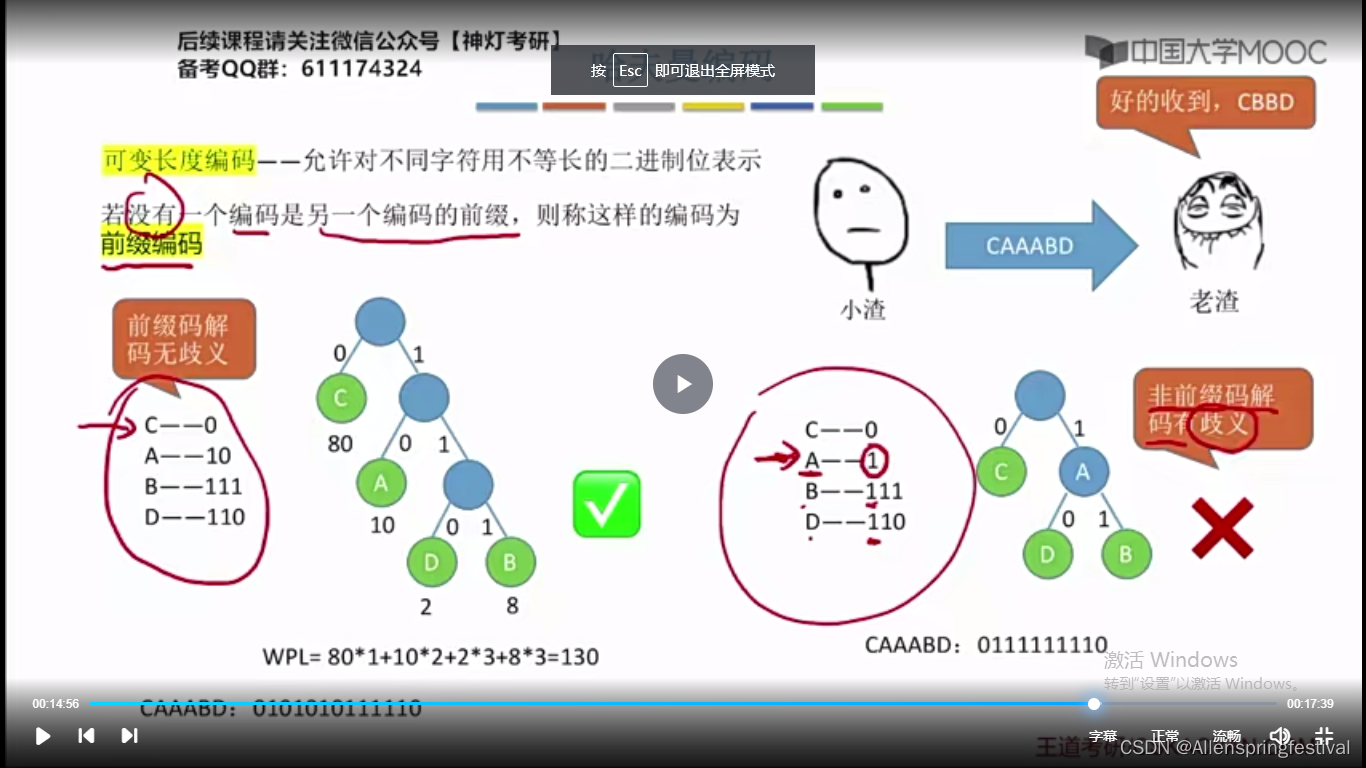
 前缀编码：若没有一个编码是另一个编码是另一个编码的前缀。

前缀编码是没有歧义的（必须是叶子结点）

 知识点回顾：