3。数据结构（1）

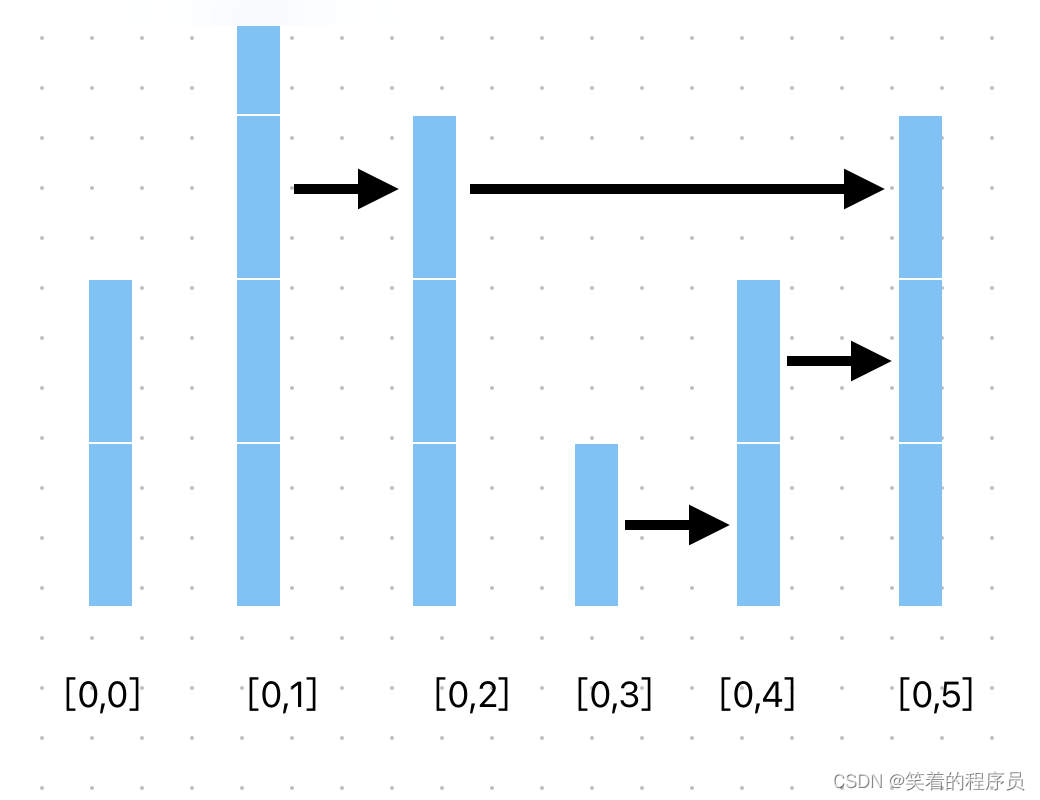
嵌入式软件开发第三部分，各类常用的数据结构及扩展，良好的数据结构选择是保证程序稳定运行的关键，（1）部分包括数组，链表，栈，队列。（2）部分包括树，堆，散列表，图。

一数组

优点：按照索引查询速度快、遍历数组方便

缺点：

1 数组大小固定后无法扩容

2 数组只能存储一种类型的数据

3 添加删除慢（需要移动其它元素）

使用场景：频繁查询，对存储空间要求不大；增加删除少的情况

所有的数组都是由连续的内存位置组成。最低的地址对应第一个元素，最高的地址对应最后一个元素。

遍历一维数组

#include <stdio.h>
 
int main ()
{
   int n[ 10 ]; /* n 是一个包含 10 个整数的数组 */
   int i,j;
 
   /* 初始化数组元素 */         
   for ( i = 0; i < 10; i++ )
   {
      n[ i ] = i + 100; /* 设置元素 i 为 i + 100 */
   }
   
   /* 输出数组中每个元素的值 */
   for (j = 0; j < 10; j++ )
   {
      printf("Element[%d] = %d\n", j, n[j] );
   }
 
   return 0;
}

1 多维数组

type name[size1][size2]...[sizeN];

二维数组

多维数组最简单的形式是二维数组。一个二维数组，在本质上，是一个一维数组的列表。声明一个 x 行 y 列的二维整型数组，形式如下：

type arrayName [ x ][ y ];

int x[3][4];

因此，数组中的每个元素是使用形式为 a[ i , j ] 的元素名称来标识的，其中 a 是数组名称，i 和 j 是唯一标识 a 中每个元素的下标。

初始化二维数组

int a[3][4] = {
{0, 1, 2, 3} ,   /* 初始化索引号为 0 的行 */
{4, 5, 6, 7} ,   /* 初始化索引号为 1 的行 */
{8, 9, 10, 11}   /* 初始化索引号为 2 的行 */
};

或

int a[3][4] = {0,1,2,3,4,5,6,7,8,9,10,11};

访问单个二维数组元素

int val = a[2][3];

上面的语句将获取数组中第 3 行第 4 个元素。您可以通过上面的示意图来进行验证。让我们来看看下面的程序，我们将使用嵌套循环来处理二维数组：

遍历二维数组

#include <stdio.h>
 
int main ()
{
   /* 一个带有 5 行 2 列的数组 */
   int a[5][2] = { {0,0}, {1,2}, {2,4}, {3,6},{4,8}};
   int i, j;
 
   /* 输出数组中每个元素的值 */
   for ( i = 0; i < 5; i++ )
   {
      for ( j = 0; j < 2; j++ )
      {
         printf("a[%d][%d] = %d\n", i,j, a[i][j] );
      }
   }
   return 0;
}

2 把数组作为参数传递给函数

如果您想要在函数中传递一个一维数组作为参数，您必须以下面三种方式来声明函数形式参数，这三种声明方式的结果是一样的，因为每种方式都会告诉编译器将要接收一个整型指针。同样地，您也可以传递一个多维数组作为形式参数。

1）形式参数是一个指针（常用）

void myFunction(int *param) { . . . }

2）形式参数是一个已定义大小的数组

void myFunction(int param[10]) { . . . }

3）形式参数是一个未定义大小的数组：（常用）

void myFunction(int param[]) { . . . }

例子

#include <stdio.h>
 
/* 函数声明 */
double getAverage(int arr[], int size);
 
int main ()
{
   /* 带有 5 个元素的整型数组 */
   int balance[5] = {1000, 2, 3, 17, 50};
   double avg;
 
   /* 传递一个指向数组的指针作为参数 */
   avg = getAverage( balance, 5 ) ;
 
   /* 输出返回值 */
   printf( "平均值是： %f ", avg );
    
   return 0;
}
 
double getAverage(int arr[], int size)
{
  int    i;
  double avg;
  double sum=0;
 
  for (i = 0; i < size; ++i)
  {
    sum += arr[i];
  }
 
  avg = sum / size;
 
  return avg;
}

3 从函数返回数组

C 语言不允许返回一个完整的数组作为函数的参数。但是，您可以通过指定不带索引的数组名来返回一个指向数组的指针。

通过声明一个返回指针的函数，从函数中返回数组

int * myFunction() { . . . }

例子：生成 10 个随机数，并使用数组来返回它们

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
 
/* 要生成和返回随机数的函数 */
int * getRandom( )
{
  static int  r[10];
  int i;
 
  /* 设置种子 */
  srand( (unsigned)time( NULL ) );
  for ( i = 0; i < 10; ++i)
  {
     r[i] = rand();
     printf( "r[%d] = %d\n", i, r[i]);
 
  }
 
  return r;
}
 
/* 要调用上面定义函数的主函数 */
int main ()
{
   /* 一个指向整数的指针 */
   int *p;
   int i;
 
   p = getRandom();
   for ( i = 0; i < 10; i++ )
   {
       printf( "*(p + %d) : %d\n", i, *(p + i));
   }
 
   return 0;
}

4 指向数组的指针

众所周知，数组名是一个指向数组中第一个元素的常量指针。因此，在下面的声明中：

double balance[50];

balance 是一个指向 &balance[0] 的指针，即数组 balance 的第一个元素的地址。因此，下面的程序片段把 p 赋值为 balance 的第一个元素的地址：

double *p;
double balance[10];

p = balance;

然后就可以使用*p、*(p+1)、*(p+2) 等来访问数组元素

访问数组

printf("*(p + %d) : %f\n", i, *(p + i) );

或

printf("*(balance + %d) : %f\n", i, *(balance + i) );

二栈

栈是一种特殊的线性表，仅能在线性表的一端操作，栈顶允许操作，栈底不允许操作。

特点： 先进后出（压子弹）

使用场景：栈常应用于实现递归功能方面的场景，例如斐波那契数列。

1、栈的定义
首先对栈进行定义，构建一个简单的结构体，采用typedef struct 的类型，然后包含栈顶、栈底和栈内元素三个部分

typedef struct{
   char data[100];
   int top;
   int bottom;
}stack;//结构体名为stack

2、栈的创建
然后是栈的构建，来为栈开辟内存空间，存储我们进行入站出栈的元素。只需在栈操作开始前进行一次栈的构建即可，无需重复。

stack *StackCreate(){
   stack *p=(stack*)malloc(sizeof(stack));//分配新空间
   if(p==NULL)//分配失败
   return 0;
   p->bottom=p->top=0;//分配成功
   return p;
}
上述代码段为向p内分配内存，成功则返回p

3、入栈（压栈）
栈构建完毕后就开始进行栈的操作了，首先就是如何将字符、数字等我们想要的内容送入栈中，就需要进行入栈操作。

void StackInput(stack *p,char str){
p->data[p->top]=str;//存入栈中
p->top++;//栈顶指针加1
}
将字符str存入栈中，位置为top，只存在data中，然后栈top++

4、出栈
当我们想要栈顶的元素时，就用到了出栈的操作

char StackOutput(stack *p,char str){
   if(p->top!=p->bottom){//栈非空
       str=p->data[p->top-1];//栈顶内容输出
       p->top--;//栈顶减1
       return str;
   }
}
因为top位置为栈顶值的下一个，因此将data中top-1的值输出，栈顶top–，返回的值为栈顶元素str

5、栈的遍历
但我们想要输出栈内存储的所有元素，那么就需要使用到遍历

void StackPrint(stack *p){
   while(p->top!=p->bottom){
       printf("%c",p->data[p->top-1]);
       p->top--;
   }
}

例子：将字符串压入栈中，然后从栈中输出

int main(){
   int i;
   stack *p;//定义栈名
   char a[10]="asdfgh";
   p=StackCreate();//创建栈
   for(i=0;i<strlen(a);i++)//将字符串a的字符入栈
   StackInput(p,a[i]);
   printf("输出栈中所有字符：\n");
   StackPrint(p);
}

#include<stdio.h>
#include<malloc.h>
#include<string.h>

//定义栈 
typedef struct{
	char data[100];
	int top;
	int bottom;
}stack;

//创建栈
stack *StackCreate(){
	stack *p=(stack*)malloc(sizeof(stack));//分配新空间 
	if(p==NULL)//分配失败 
	return 0;
	p->bottom=p->top=0;//分配成功 
	return p;
}

//入栈
void StackInput(stack *p,char str){
	p->data[p->top]=str;//存入栈中 
	p->top++;//栈顶指针加1 
} 

//出栈 
char StackOutput(stack *p,char str){
	if(p->top!=p->bottom){//栈非空 
		str=p->data[p->top-1];//栈顶内容输出 
		p->top--;//栈顶减1 
		return str;
	}
} 

//输出 
void StackPrint(stack *p){
	while(p->top!=p->bottom){
		printf("%c",p->data[p->top-1]);
		p->top--;
	}
}

//主函数 
int main(){
	int i;
	stack *p;//定义栈名 
	char a[10]="asdfgh";
	p=StackCreate();//创建栈 	 
	for(i=0;i<strlen(a);i++)//将字符串a的字符入栈 
	StackInput(p,a[i]);
	printf("输出栈中所有字符：\n"); 
	StackPrint(p);
}

三队列（Queue）

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（head）进行删除操作，而在表的后端（tail）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

特点：先进先出（漏桶算法）

使用场景：因为队列先进先出的特点，在多线程阻塞队列管理中非常适用。

使用链表来实现队列

1.头文件

所用标准库

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>

定义结构体

typedef int QDateType;//队列存储数据类型

typedef struct QueueNode //队列元素节点
{
   QDateType val;
   struct QueueNode* next;
}QueueNode;

typedef   struct Queue //队列
{
   QueueNode* head;
   QueueNode* tail;
}Queue;

函数声明

void QueueInti(Queue* pq);
// 队列初始化
void QueueDestory(Queue* pq);
// 队列的销毁
void QueuePush(Queue* pq, QDateType x);
// 入队
void QueuePop(Queue* pq);
// 出队
QDateType QueueFront(Queue* pq);
// 取出队首元素
int QueueSize(Queue* pq);
// 求队列的长度
bool QueueEmpty(Queue* pq);
// 判断队是否为空

2 各功能函数的实现

队列的初始化，将头、尾置为空指针即可

void QueueInti(Queue* pq)
{
	assert(pq); //防止pq为空指针
	pq->head = pq->tail = NULL;
}

队列的销毁，遍历队列元素，然后将每一个元素释放。

void QueueDestory(Queue* pq)
{
	assert(pq); //防止pq为空指针
	QueueNode* cur = pq->head;
	while (cur)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->tail = pq->head = NULL;
}

入队，对于入队，我们首先需要去开辟一个新的节点来存储数据，然后将这个节点加入到tail后即可。此时我们就要分别考虑。

如果为空队列，那么我们不仅要改变tail，还要改变head的值（head = tail）
如果不为空队列，只用改变tail即可。

void QueuePush(Queue* pq, QDateType x)
{
	assert(pq); //防止pq为空指针

	QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
	if (NULL == newNode)
	{
		printf("malloc error\n");
		exit(-1);
	}
	newNode->val = x;
	newNode->next = NULL;//开辟一个新节点存储数据

	if (pq->tail == NULL)//判断是否为空队列
	{
		assert(pq->head == NULL);
		pq->head = pq->tail = newNode;
	}
	else
	{
		pq->tail->next = newNode;
		pq->tail = newNode;
	}
}

出队，同样需要考虑两种情况

队列为空，改变head的同时改变tail（head = tail）
队列不为空，改变head即可。

void QueuePop(Queue* pq)
{
	assert(pq);//防止pq为空指针
	assert(pq->head && pq->tail); //防止队列为空队列
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QueueNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
}

取出队首元素，直接访问头节点取出即可

QDateType QueueFront(Queue* pq)
{
	assert(pq);//防止pq为空指针
	assert(pq->head && pq->tail); //防止队列为空队列

	return pq->head->val;
}

判断是否为空队列，只需要判断头指针是否为NULL，如果是则为空

bool QueueEmpty(Queue* pq)
{
	assert(pq);

	return pq->head == NULL;
}

求队伍长度，创建一个变量，遍历队伍求长度。

int QueueSize(Queue* pq)
{
	assert(pq);
	QueueNode* cur = pq->head;
	int count = 0;
	while (cur)
	{
		cur = cur->next;
		count++;
	}
	return count;
}

用链表实现队列（先进先出）完整代码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>

typedef int QDateType;

typedef struct QueueNode
{
	QDateType val;
	struct QueueNode* next;
}QueueNode;

typedef	struct Queue
{
	QueueNode* head;
	QueueNode* tail;
}Queue;

void QueueInti(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
}

void QueueDestory(Queue* pq)
{
	assert(pq);
	QueueNode* cur = pq->head;
	while (cur)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->tail = pq->head = NULL;
}

void QueuePush(Queue* pq, QDateType x)
{
	assert(pq);

	QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
	if (NULL == newNode)
	{
		printf("malloc error\n");
		exit(-1);
	}
	newNode->val = x;
	newNode->next = NULL;

	if (pq->tail == NULL)
	{
		assert(pq->head == NULL);
		pq->head = pq->tail = newNode;
	}
	else
	{
		pq->tail->next = newNode;
		pq->tail = newNode;
	}

}

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->head && pq->tail);
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QueueNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
}

bool QueueEmpty(Queue* pq)
{
	assert(pq);

	return pq->head == NULL;
}

QDateType QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->head);

	return pq->head->val;
}

int QueueSize(Queue* pq)
{
	assert(pq);
	QueueNode* cur = pq->head;
	int count = 0;
	while (cur)
	{
		cur = cur->next;
		count++;
	}
	return count;
}

四链表（基于链表实现队列和栈）

链表是物理存储单元上非连续的、非顺序的存储结构，数据元素的逻辑顺序是通过链表的指针地址实现，每个元素包含两个结点，一个是存储元素的数据域（内存空间），另一个是指向下一个结点的指针域。根据指针的指向，链表能形成不同的结构。例如：单链表，双向链表，循环链表等。

优点：

很常用的一种数据结构，不需要初始化容量，可以任意加减元素；
添加或删除元素时只需要改变前后两个元素结点的指针域指向地址即可，所以添加删除速度很快。

缺点：

因含有大量的指针域，占用空间较大；

查找元素需要遍历链表来查找，非常耗时。

使用场景：数据量较小，需要频繁添加删除操作的场景。

8种链表结构

循环带头单链表

循环带头双向链表

循环不带头单链表

循环不带头双向链表

非循环带头单链表

非循环带头双向链表

非循环不带头单链表

非循环不带头双向链表

（1）单向或者双向

（2）带头或者不带头

（3）循环或者非循环

常用的为

非循环不带头单链表

头文件及函数声明

// 1、无头+单向+非循环链表增删查改实现
typedef int SLTDateType;
typedef struct SListNode
{
 SLTDateType data;
 struct SListNode* next;
}SListNode;
 
// 动态申请一个节点
SListNode* BuySListNode(SLTDateType x);
// 单链表打印
void SListPrint(SListNode* plist);
// 单链表尾插
void SListPushBack(SListNode** pplist, SLTDateType x);
// 单链表的头插
void SListPushFront(SListNode** pplist, SLTDateType x);
// 单链表的尾删
void SListPopBack(SListNode** pplist);
// 单链表头删
void SListPopFront(SListNode** pplist);
// 单链表查找
SListNode* SListFind(SListNode* plist, SLTDateType x);
// 单链表在pos位置之后插入x
void SListInsertAfter(SListNode* pos, SLTDateType x);
// 单链表删除pos位置之后的值
void SListEraseAfter(SListNode* pos);

申请内存函数


SListNode* BuySListNode(SLTDateType x)
{
	SListNode* tmp = (SListNode*)malloc(sizeof(SListNode));
	if (tmp == NULL)
	{
		printf("无法给节点开辟空间\n");
		return NULL;
	}
	else
	{
		tmp->data = x;
		tmp->next = NULL;
		return tmp;
	}
}

打印单链表内容函数

// 单链表打印
void SListPrint(SListNode* plist)
{
	SListNode* head = plist;
	while (head != NULL)
	{
		printf("%d ", head->data);
		head = head->next;
	}
}

单链表尾部插入函数

// 单链表尾插
void SListPushBack(SListNode** pplist, SLTDateType x)
{
	
	SListNode* newnode = BuySListNode(x);
	if ( *pplist== NULL)
	{
		*pplist = newnode;
	}
	else
	{
		SListNode* tail = *pplist;
		while (tail->next != NULL)
		{
			tail = tail->next;
		}
		tail->next = newnode;
	}
}

单链表尾部删除函数

// 单链表的尾删
void SListPopBack(SListNode** pplist)
{
	assert(*pplist);
	SListNode* cur = *pplist;
	SListNode* prev = NULL;
	if (cur->next == NULL)
	{
		free(cur);
		*pplist = NULL;
	}
	else
	{
		while (cur->next != NULL)
		{
			prev = cur;
			cur = cur->next;
		}
		free(cur);
		prev->next = NULL;
	}
}

单链表头部插入函数

// 单链表的头插
void SListPushFront(SListNode** pplist, SLTDateType x)
{
	SListNode* newnode = BuySListNode(x);
	if (*pplist == NULL)
	{
		*pplist = newnode;
	}
	else
	{
		newnode->next = *pplist;
		*pplist = newnode;
	}
}

单链表头部删除函数

// 单链表头删
void SListPopFront(SListNode** pplist)
{
	assert(*pplist);
	SListNode* cur = *pplist;
	if ((*pplist)->next == NULL)
	{
		free(*pplist);
		*pplist = NULL;
	}
	else
	{
		cur = cur->next;
		free(*pplist);
		*pplist = cur;
	}
}

单链表查找函数

// 单链表查找
SListNode* SListFind(SListNode* plist, SLTDateType x)
{
	assert(plist);
	while (plist != NULL)
	{
		if (plist->data == x)
		{
			return plist;
		}
		plist = plist->next;
	}
	return NULL;
}

单链表在 pos 位置之后插入x 函数

// 单链表在pos位置之后插入x
void SListInsertAfter(SListNode* pos, SLTDateType x)
{
	assert(pos);
	SListNode* newnode = BuySListNode(x);
		newnode->next = pos->next;
		pos->next = newnode;
}

单链表删除 pos 位置之后的值函数

// 单链表删除pos位置之后的值
void SListEraseAfter(SListNode* pos)
{
	assert(pos);
	if (pos->next == NULL)
	{
		printf("后面无数据\n");
		return;
	}
	else
	{
		SListNode* prev = pos;
		SListNode* cur = pos->next;
		prev->next = cur->next;
		free(cur);
		cur = NULL;
	}
 
}

循环带头双向链表

头文件及函数声明

// 2、带头+双向+循环链表增删查改实现
typedef int LTDataType;
typedef struct ListNode 
{
	ListDateType val;
	struct ListNode* prev;
	struct ListNode* next;
}ListNode;	
 
//初始化双向链表
ListNode* ListInit(ListNode* phead);
//双向链表打印
void ListPrint(ListNode* phead);
// 创建返回链表的头结点.
ListNode* BuyList(ListDateType x);
//双向链表尾插
void ListPushBack(ListNode* phead,ListDateType x);
//双向链表尾删
void ListPopBack(ListNode* phead);
//双向链表头插
void ListPushFront(ListNode* phead, ListDateType x);
//双向链表头删
void ListPopFront(ListNode* phead);
//双向链表查找
ListNode* ListFind(ListNode* pHead, ListDateType x);
//在pos之前插入
void ListInsert(ListNode* pos, ListDateType x);
//删除pos位置
void ListErase(ListNode* pos);

初始化双向链表函数

//初始化双向链表
ListNode* ListInit(ListNode* phead)
{
	phead = BuyList(0);
	phead->next = phead;
	phead->prev = phead;
	return phead;
}

双向链表打印函数

//双向链表打印
void ListPrint(ListNode* phead)
{
	ListNode* cur = phead->next;
	while (cur != phead)
	{
		printf("%d ", cur->val);
		cur = cur->next;
	}
 
}

返回链表的头节点函数

返回链表的头节点是非常重要的，因为它是整个链表的入口。通过获取链表的头节点，可以迅速访问链表的所有节点，并对这些节点进行操作。

在很多链表应用中，我们需要遍历整个链表或者将整个链表反转，而这些操作都需要通过获取链表头节点来实现。同时，当我们需要对链表进行删除、插入或修改等操作时，我们也需要知道链表的头节点才能进行这些操作。

此外，许多算法问题也需要要求返回链表的头节点，例如找到链表的倒数第k个节点、判断链表是否存在环等问题，都需要访问链表的头节点。

因此，获取链表的头节点是基于链表进行各种操作和解决问题的基础，是链表操作的必备步骤之一。

// 创建返回链表的头结点
ListNode* BuyList(ListDateType x)
{
	ListNode* newnode = (ListNode*)malloc(sizeof(ListNode));
	if (newnode == NULL)
	{
		printf("BuyList fail\n");
		exit(-1);
	}
	newnode->val = x;
	newnode->next = NULL;
	newnode->prev = NULL;
    return newnode;
}

双向链表尾部插入函数

//双向链表尾插
void ListPushBack(ListNode* phead, ListDateType x)
{
	assert(phead);
	ListNode* newnode = BuyList(x);
	ListNode* tail = phead->prev;
 
	tail->next = newnode;
	phead->prev = newnode;
	newnode->next = phead;
	newnode->prev = tail;
}

双向链表尾部删除函数

//双向链表尾删
void ListPopBack(ListNode* phead)
{
	assert(phead->next != phead);
	ListNode* tail = phead->prev;
	ListNode* prev = tail->prev;
	phead->prev = prev;
	prev->next = phead;
	free(tail);
	tail = NULL;
}

双向链表头部插入函数

//双向链表头插
void ListPushFront(ListNode* phead, ListDateType x)
{
	assert(phead);
	ListNode* newnode = BuyList(x);
	ListNode* head = phead->next;
 
	phead->next = newnode;
	head->prev = newnode;
	newnode->next = head;
	newnode->prev = phead;
}

双向链表头部删除函数

//双向链表头删
void ListPopFront(ListNode* phead)
{
	assert(phead);
	assert(phead->next != phead);
 
	ListNode* head = phead->next;
	ListNode* next = head->next;
 
	phead->next = next;
	next->prev = phead;
	free(head);
	head = NULL;
}

双向链表查找函数

//双向链表查找
ListNode* ListFind(ListNode* phead, ListDateType x)
{
	assert(phead);
	assert(phead->next != phead);
	ListNode* pos = phead->next;
	while (pos != phead)
	{
		if (pos->val == x)
		{
			return pos;
		}
		pos = pos->next;
	}
	return NULL;
}

单链表在 pos 位置之后插入x 函数

//在pos之前插入
void ListInsert(ListNode* pos, ListDateType x)
{
	assert(pos);
	ListNode* newnode = BuyList(x);
	ListNode* prev = pos->prev;
 
	prev->next = newnode;
	pos->prev = newnode;
	newnode->prev = prev;
	newnode->next = pos;
}

单链表删除 pos 位置之后的值函数

//删除pos位置
void ListErase(ListNode* pos)
{
	assert(pos);
	ListNode* prev = pos->prev;
	ListNode* next = pos->next;
	prev->next = next;
	next->prev = prev;
	free(pos);
	pos = NULL;
}