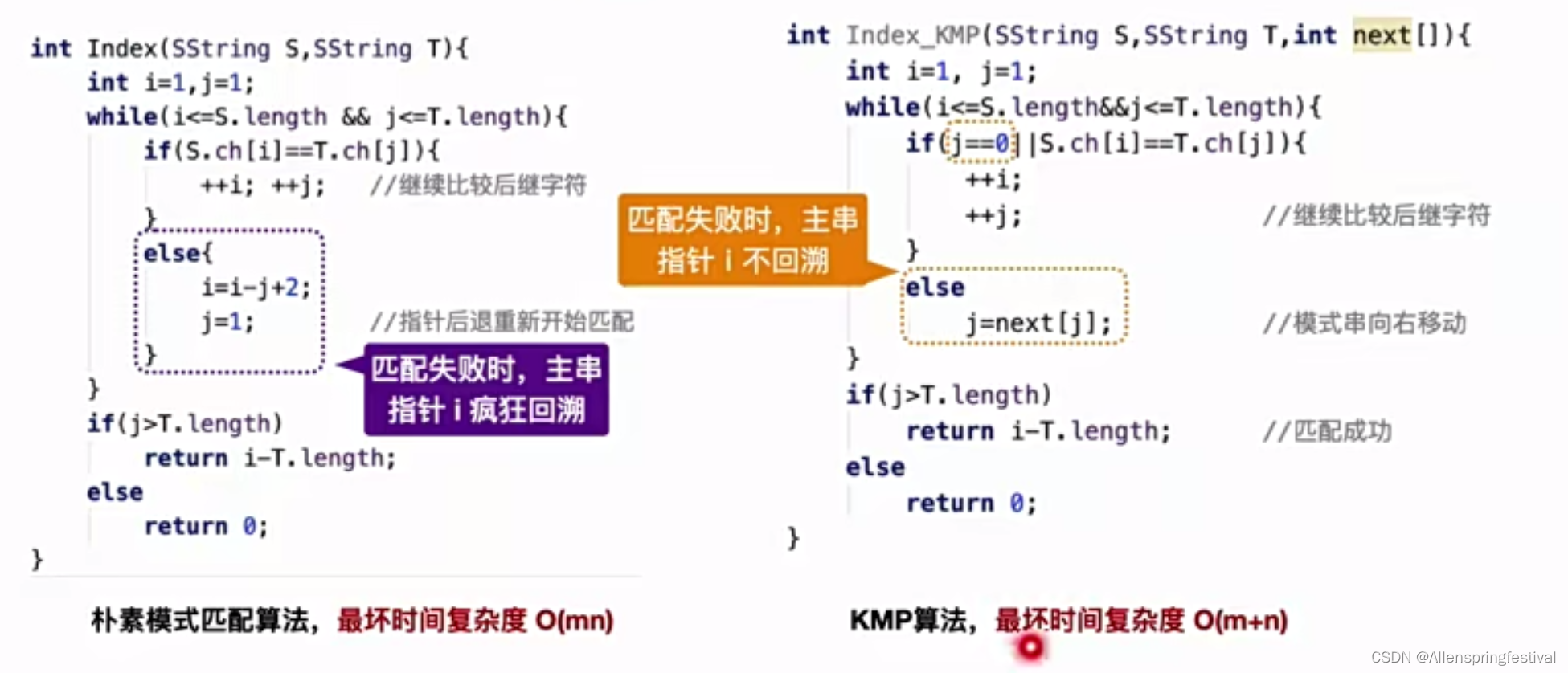
对朴素模式匹配算法的优化:

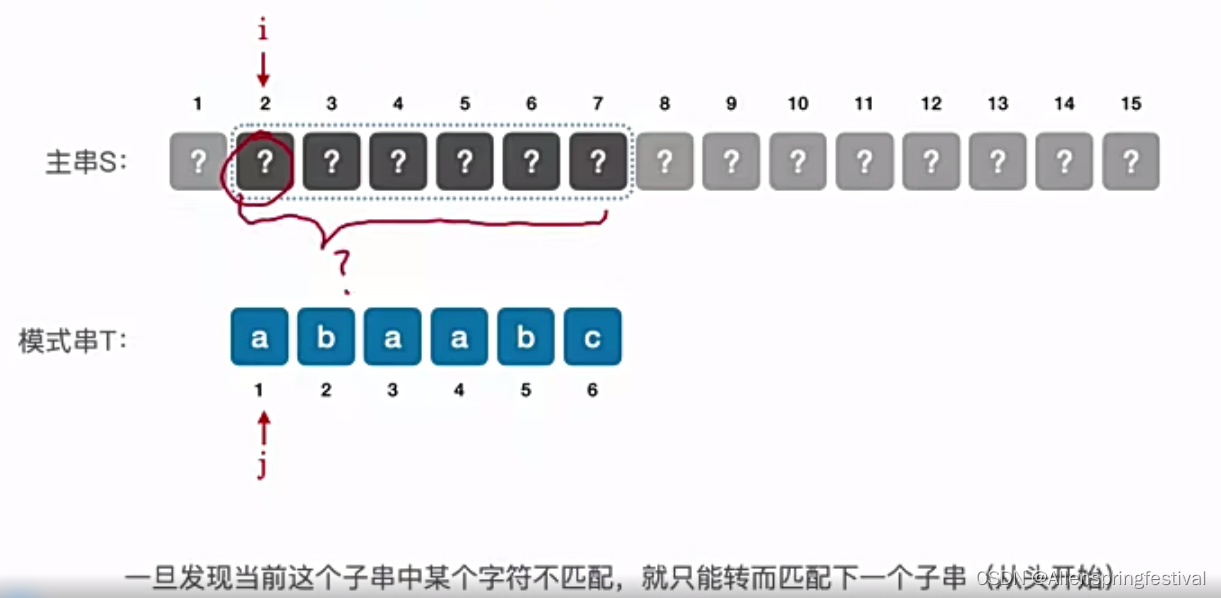


当我们匹配最后一个字符才发现匹配失败。
那么前面这些字符一定是与模式串对应的。

通过模式串的部分匹配

朴素模式匹配算法优化思路:

不匹配的字符之前,一定是和模式串一致的。


可以跳过中间好几个没有必要的对比
前面5个已知字符中我们已知ab当i=4和i=5时。

我们得到的结论并不依赖于主串,只与模式串有关。
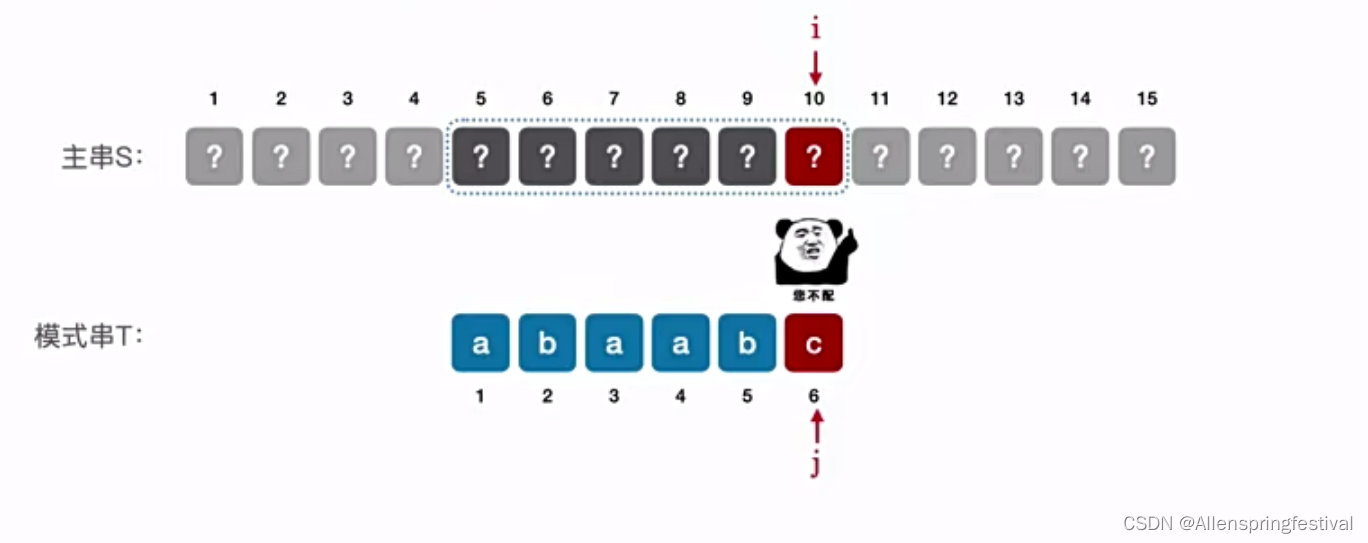
前面这几个字符肯定是与模式串匹配的。


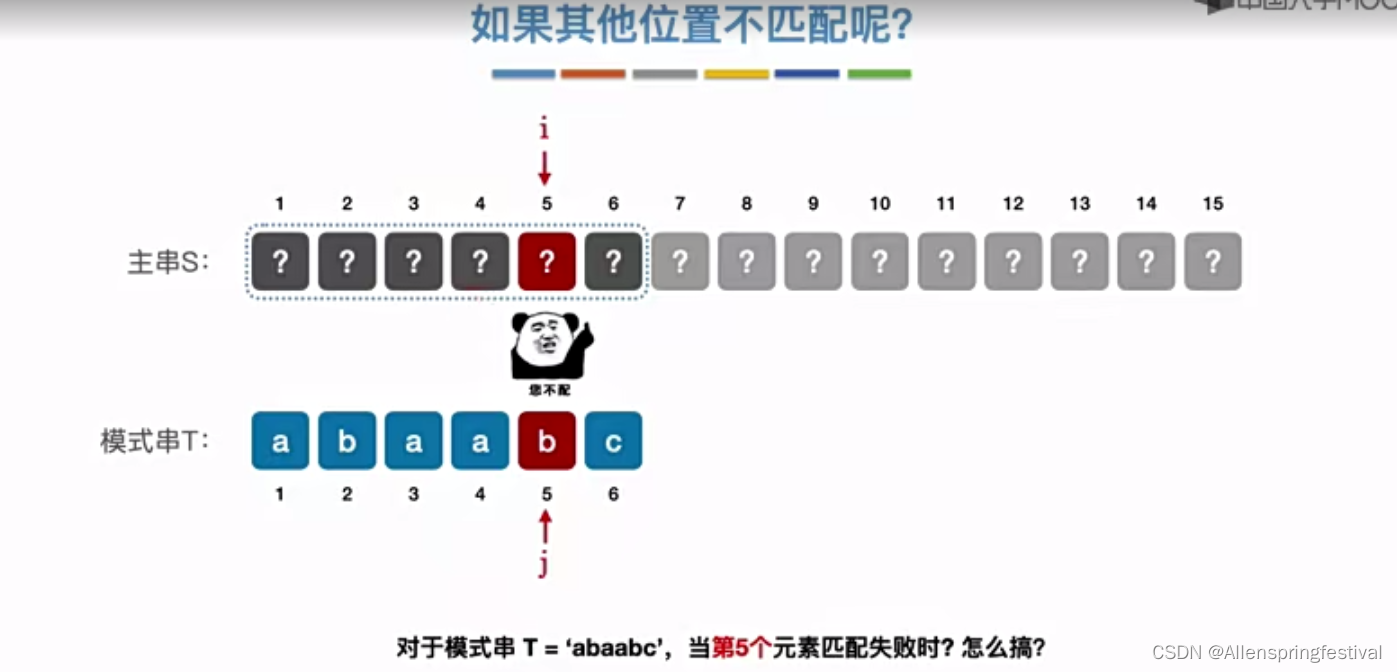
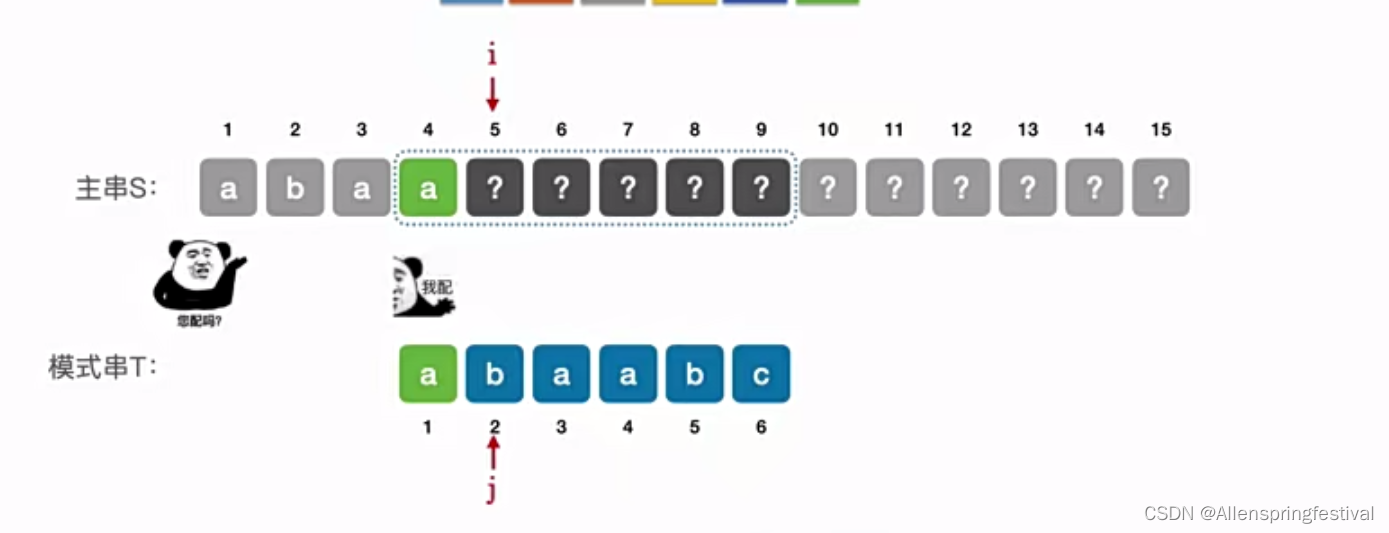
当第五个元素匹配失败后,主串指针i保持不变,模式串指针j=2
那如果第4个元素匹配失败呢?
主串指针i保持不变,模式串指针j=2

可令主串指针i不变,模式串指针j=1



IN CONCLUSION

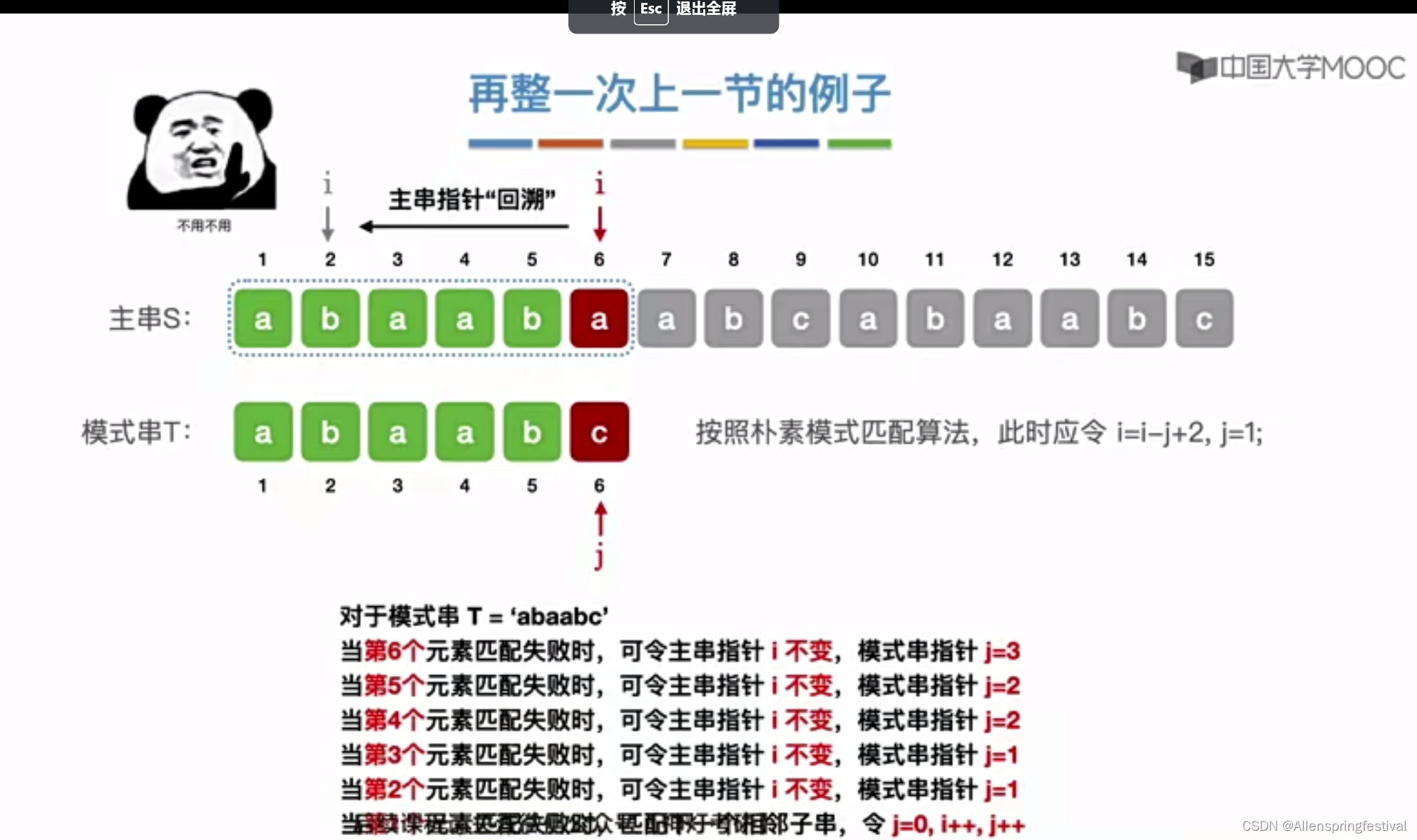
现在呢,我们知道当第六个元素匹配失败,可令主串指针i不变,模式串指针j=3。
那我们接下来改一下例子哈
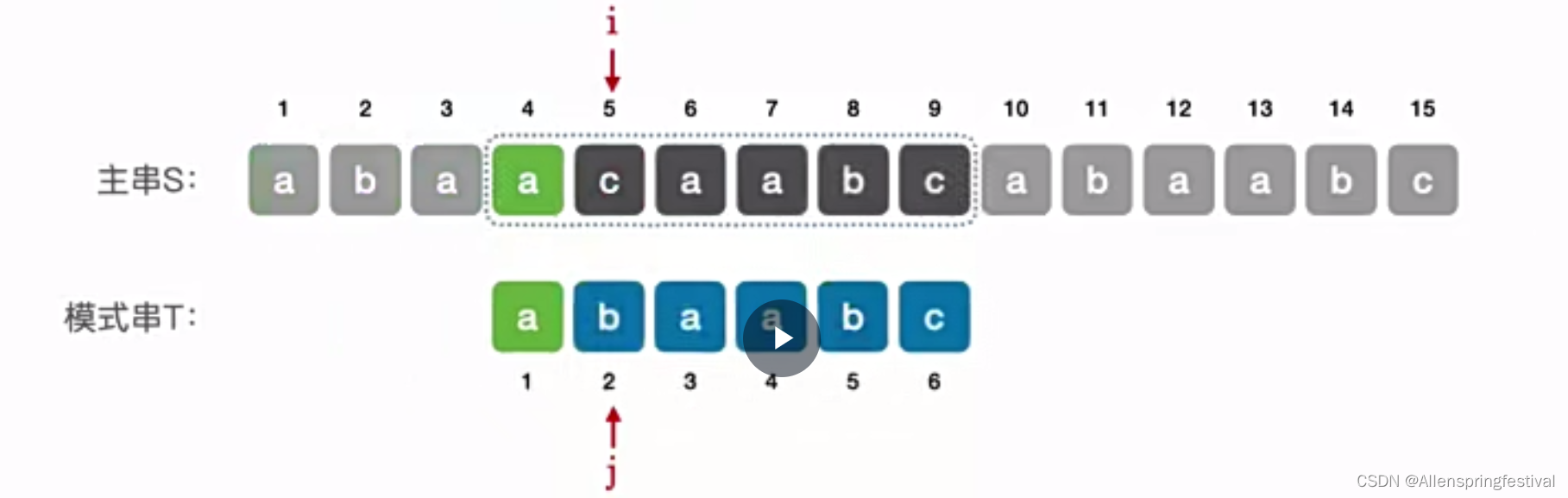
我们发现第5个元素匹配失败,那接下来令主串指针i不变,模式串指针j=2。
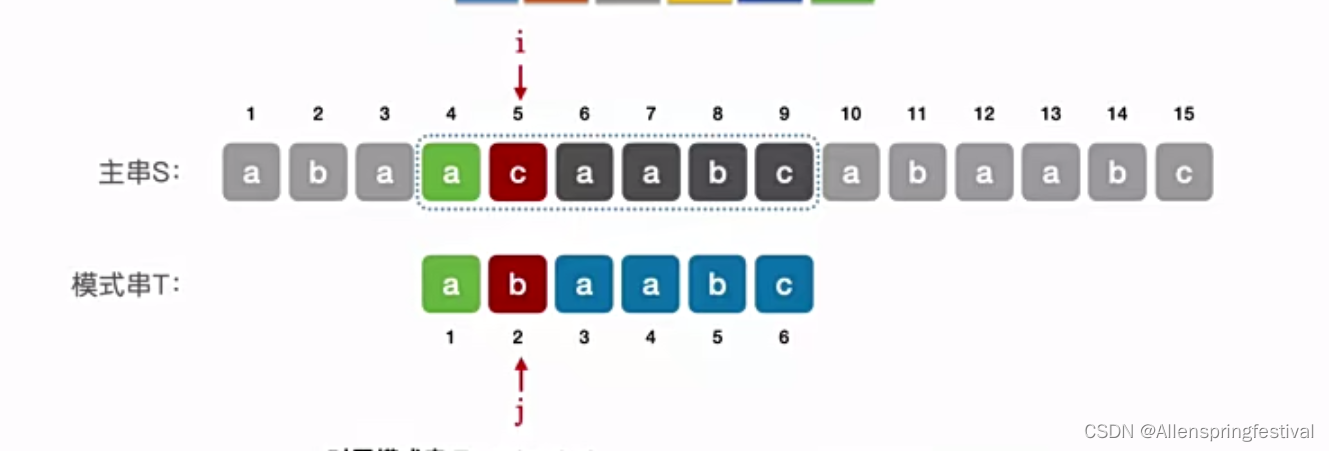
我们发现第2个元素发生失配,令主串指针i不变,模式串指针j=1.
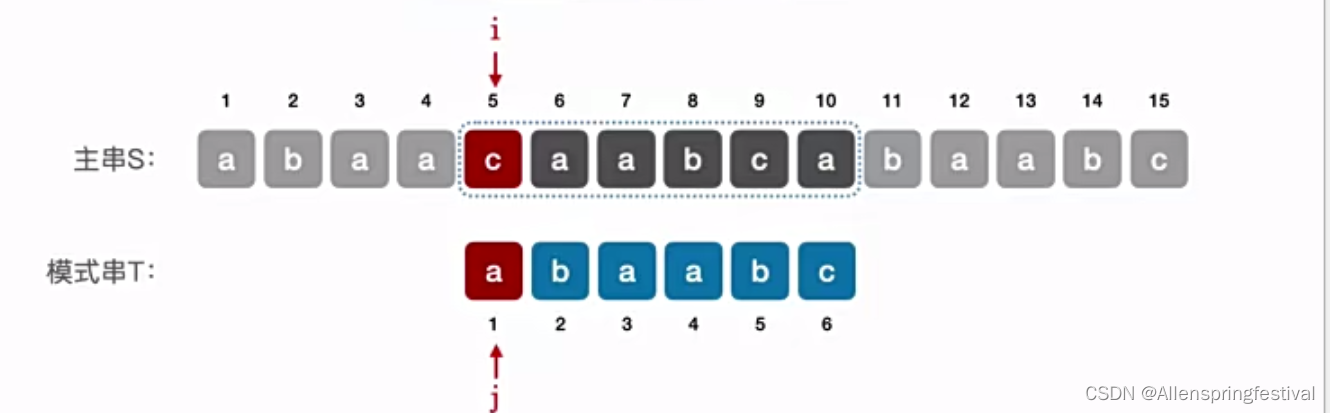
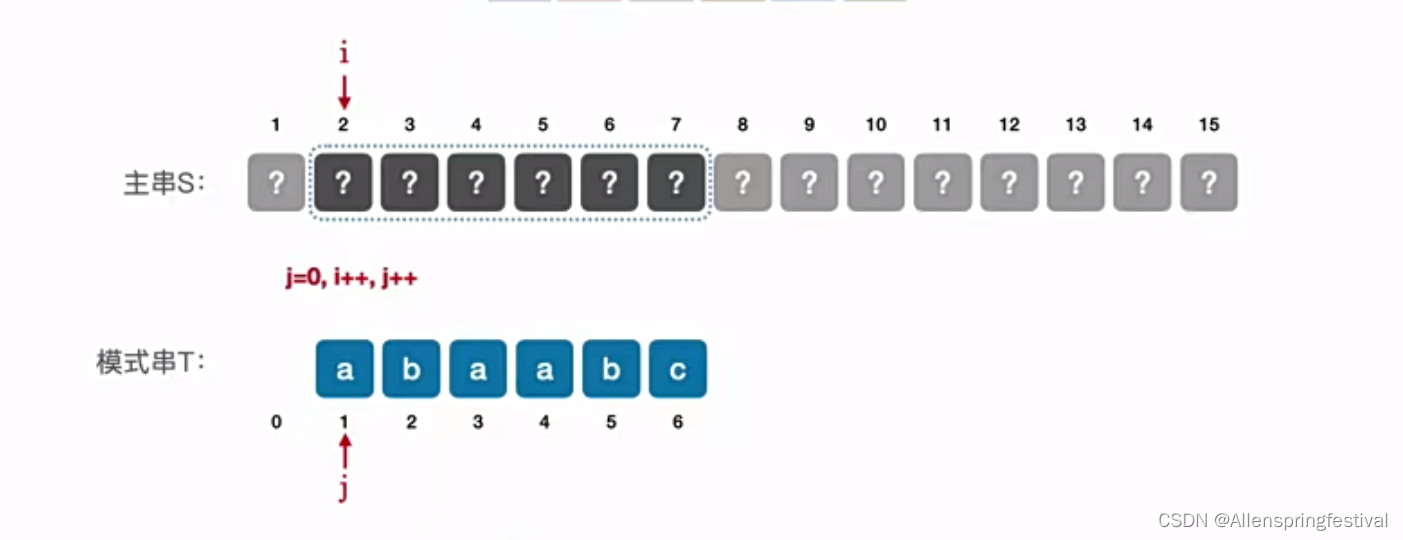
第一个元素匹配失败,匹配下一个相邻字串,令j=0,i++,j++

中间省略,与上述相同。if
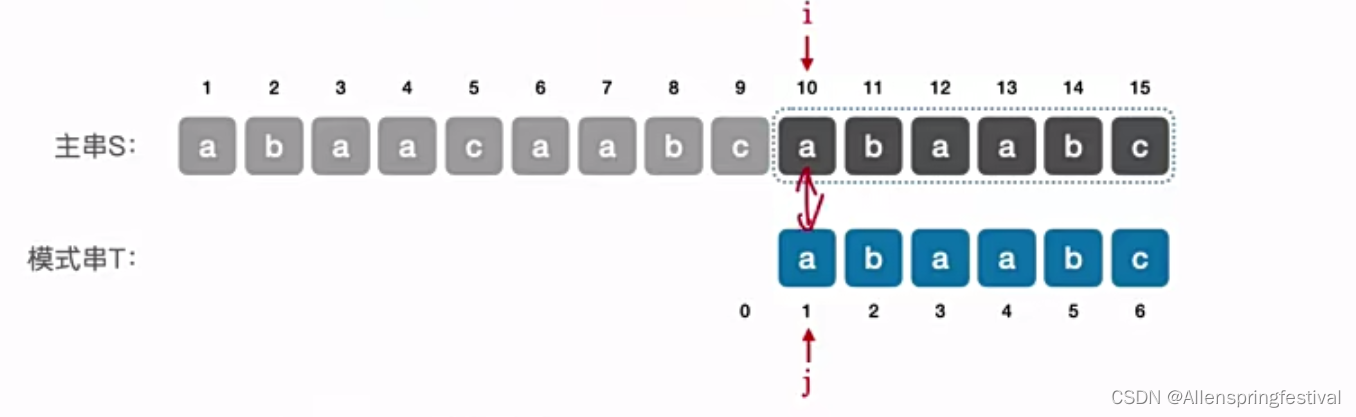
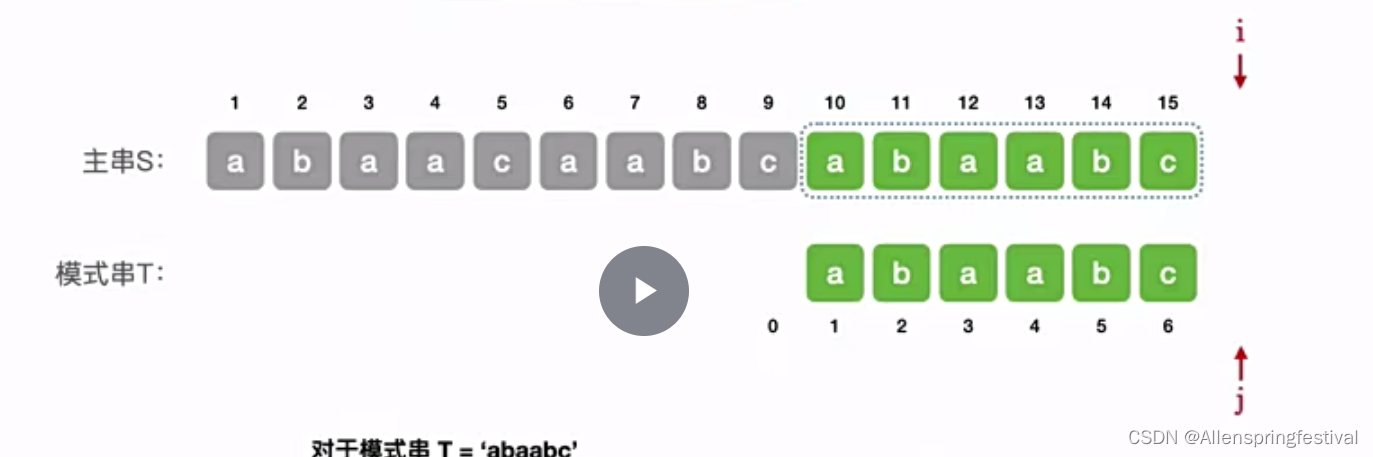
此时j超过了模式串的匹配范围而停止。


这个算法指对模式串T="abaabc"生效
第i个元素匹配失效,next[i]
模式串指针的数值由next数组存储。

这就是KMP算法
特殊情况下,if(j==0){i++;j++}
process:
(1)根据模式串T,求出next数组。
(2)利用next数组进行匹配(主串指针不回溯)

传入主串S,模式串T,以及与模式串相关的next数组。
我们来进行一个对比
 改变的只是我们圈起来的部分。
改变的只是我们圈起来的部分。