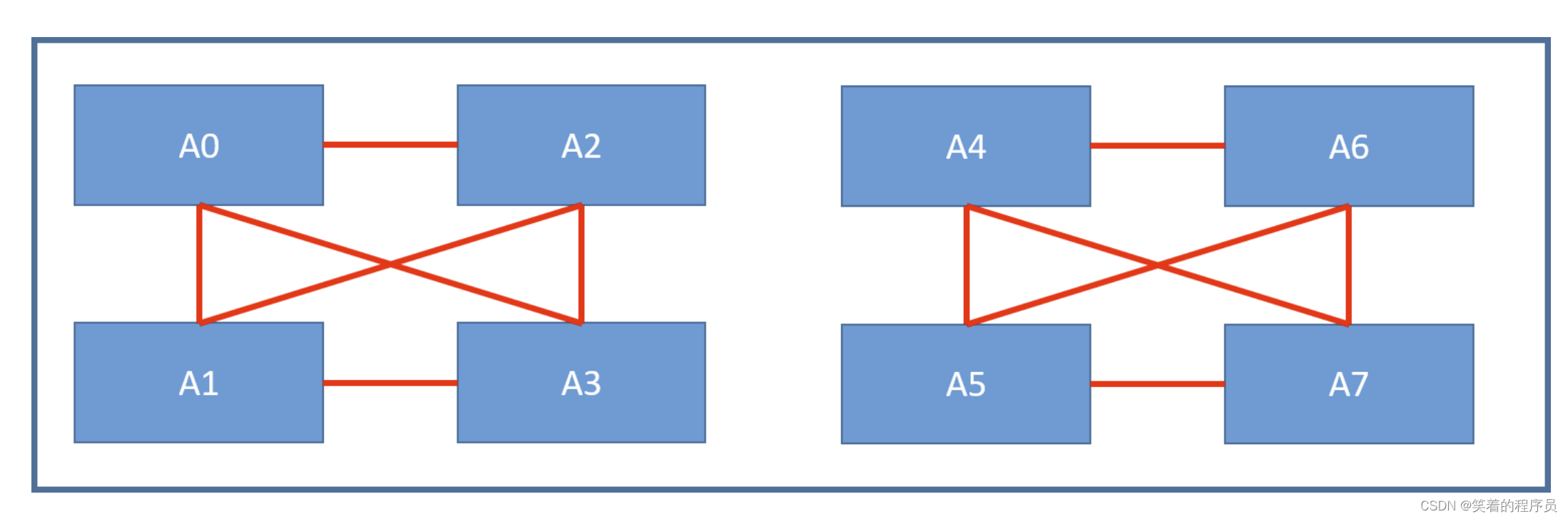
什么是二分图

1. 从离散数学的角度理解：

A ---R---> B，B ---R---> A，且A、B自身不存在R关系，那么这种R关系对应的图就是二分图

二分图是一种无向图

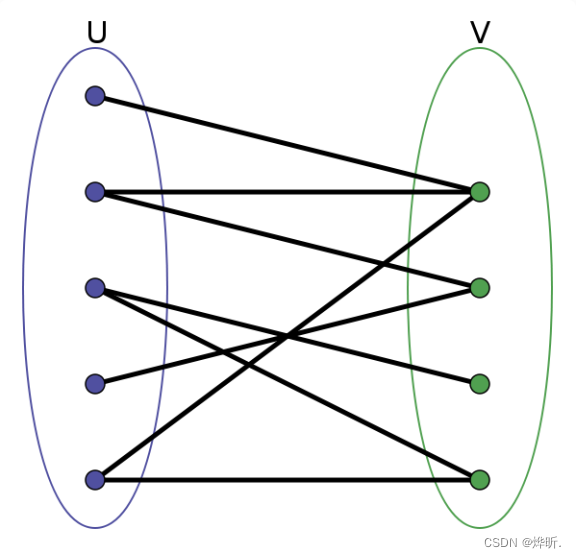
 2. 从染色问题角度

你会发现：

奇数个结点无法完成染色 => 不会是二分图

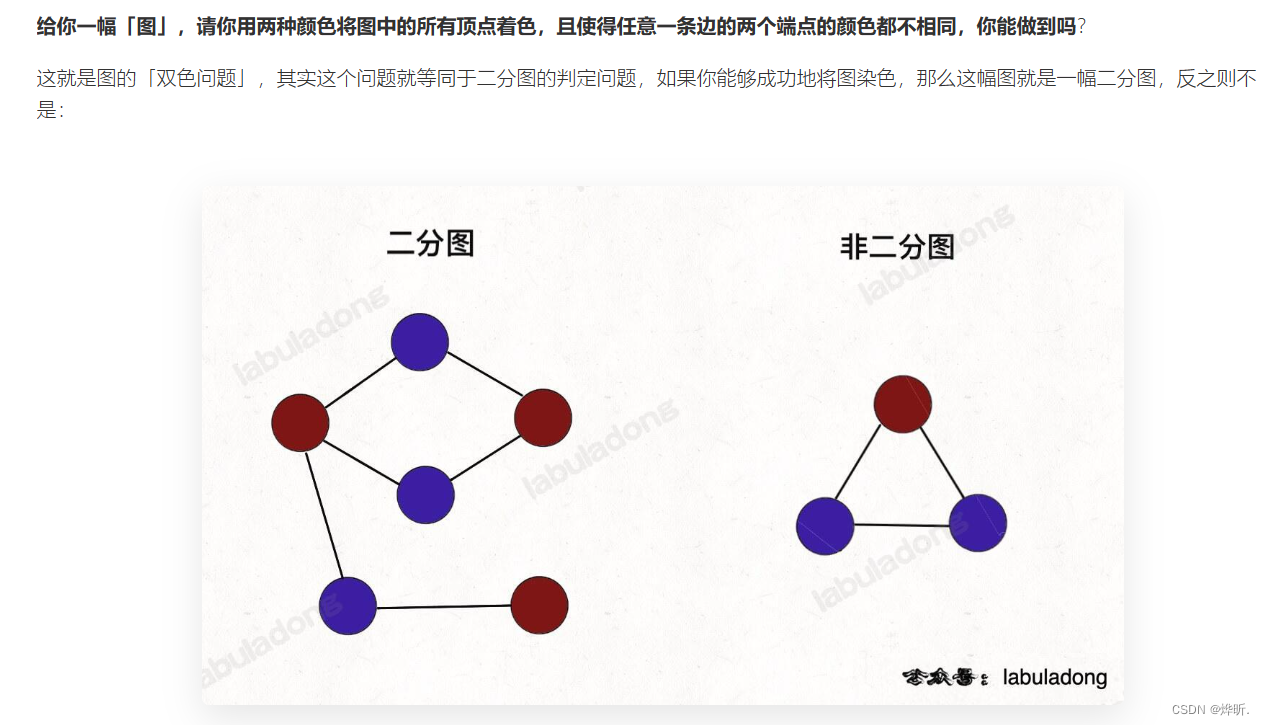
 然后本文的代码实现思路就是依据染色角度实现

代码实现

DFS

class Solution {
public:
    bool ok = true;
    vector<bool> visited;
    vector<bool> color;
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        visited.resize(n);
        color.resize(n);
        for(int i = 0; i < n; i++) {
            DFS(graph, i);
        }
        return ok;
    }

    void DFS(vector<vector<int>>& graph, int now) {
        if(!ok) return;
        visited[now] = true;
        for(auto next: graph[now]) {
            if(!visited[next]) {
                color[next] = !color[now];
                DFS(graph, next);
            }else {
                if(color[next] == color[now]) ok = false;
            }
        }
    }
};

BFS

class Solution {
public:
    bool ok = true;
    vector<bool> color;
    vector<bool> visited;
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        color.resize(n);
        visited.resize(n);
        for(int i = 0; i < n; i++) {
            BFS(graph, i);
        }
        return ok;
    }

    void BFS(vector<vector<int>>& graph, int start) {
        queue<int> q;
        visited[start] = true;
        q.push(start);
        while(!q.empty()) {
            int cur = q.front();
            q.pop();
            for(auto next: graph[cur]) {
                if(!visited[next]) {
                    visited[next] = true;
                    q.push(next);
                    color[next] = !color[cur];
                }else {
                    if(color[next] == color[cur]) {
                        ok = false;
                        return;
                    }
                }
            }
        }
    }
};

 886. 可能的二分法 - 力扣（LeetCode）

把每个人看做节点，相互讨厌的关系看做图中的边，那么 dislikes 数组就可以构成一幅图；

(相互 => 双向图 => 无向图)

又因为题目说互相讨厌的人不能放在同一组里，相当于图中的所有相邻节点都要放进两个不同的组；

那就回到了「双色问题」，如果能够用两种颜色着色所有节点，且相邻节点颜色都不同，那么你按照颜色把这些节点分成两组不就行了嘛。

需要注意的是:

这题编号是从1开始，并非程序员熟悉的从0开始

建图的时候注意二分图是无向图

 DFS

class Solution {
public:
    vector<vector<int>> graph;
    vector<bool> visited;
    vector<bool> color;
    bool ok = true;
    bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
        visited.resize(n + 1);
        color.resize(n + 1);
        buildGraph(n + 1, dislikes);
        for(int i = 1; i <= n; i++) {
            DFS(i);
        }
        return ok;
    }
    
    void buildGraph(int num, vector<vector<int>>& dis) {
        graph.resize(num);
        for(auto d: dis) {
            graph[d[0]].emplace_back(d[1]);
            graph[d[1]].emplace_back(d[0]);
        }
    }

    void DFS(int now) {
        if(!ok) return;
        visited[now] = true;
        for(auto next: graph[now]) {
            if(!visited[next]) {
                color[next] = !color[now];
                DFS(next);
            }else {
                if(color[next] == color[now]) ok = false;
            }
        }
    }
};

BFS

class Solution {
public: 
    vector<vector<int>> graph;
    vector<bool> visited;
    vector<bool> color;
    bool ok = true;
    bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
        visited.resize(n + 1);
        color.resize(n + 1);
        buildGraph(n + 1, dislikes);
        for(int i = 1; i <= n; i++) {
            BFS(i);
        }
        return ok;
    }

    void buildGraph(int num, vector<vector<int>>& dis) {
        graph.resize(num);
        for(auto d: dis) {
            graph[d[0]].emplace_back(d[1]);
            graph[d[1]].emplace_back(d[0]);
        }
    }

    void BFS(int start) {
        queue<int> q;
        q.push(start);
        visited[start] = true;
        while(!q.empty()) {
            int cur = q.front();
            q.pop();
            for(auto next: graph[cur]) {
                if(!visited[next]) {
                    visited[next] = true;
                    color[next] = !color[cur];
                    q.push(next);
                }else {
                    if(color[next] == color[cur]) {
                        ok = false;
                        return;
                    }
                }
            }
        }
    }
};