摘要

  在电子商务行业，利用丰富的历史行为数据更好地提取用户兴趣对于构建在线广告系统的点击率(CTR)预测模型至关重要。关于用户行为数据有两个关键观察结果：i) 多样性(diversity)。用户在访问电子商务网站时对不同种类的商品感兴趣。ii) 局部激活(local activation)。用户是否点击商品仅取决于他们相关的历史行为的一部分。然而，大多数传统的 CTR 模型缺乏捕获这些行为数据结构。在本文中，我们介绍了一种新提出的模型，即深度兴趣网络(DIN)，该模型是在阿里巴巴的展示广告系统中开发和部署的。DIN以兴趣分布代表用户的不同兴趣，并设计了一个类似注意力的网络结构，根据候选广告局部激活相关兴趣，证明是有效的，并且明显优于传统模型。在训练这种大规模稀疏输入的工业深度网络时，很容易遇到过拟合问题。我们仔细研究了这个问题，并提出了一种有用的自适应正则化技术。

• 多样性(diversity)。用户在访问电子商务网站时对不同种类的商品感兴趣
• 局部激活(local activation)。用户是否点击商品仅取决于他们相关的历史行为的一部分。
• DIN以兴趣分布代表用户的不同兴趣，并设计了一个类似注意力的网络结构，根据候选广告局部激活相关兴趣，证明是有效的，并且明显优于传统模型。
• 提出了一种有用的自适应正则化技术防止模型过拟合

1.引言

  广告业务每年为阿里巴巴带来数十亿美元的收入。 在每次点击费用 (CPC) 广告系统中，广告按 eCPM(每千次有效成本)排名，该 eCPM 是投标价格和 CTR(点击率)的乘积。 因此，点击率预测模型的性能直接影响最终收入，在广告系统中起着关键作用。

  在深度学习在图像识别、计算机视觉和自然语言处理方面取得成功的推动下，已经针对 CTR 预测任务提出了许多基于深度学习的方法。这些方法通常首先在输入上使用嵌入层，将原始大规模稀疏 id 特征映射到分布式表示，然后添加全连接层(即多层感知器，MLP)来自动学习特征之间的非线性关系。与传统常用的逻辑回归模型相比。 MLPs可以减少很多特征工程，这项工作在行业应用中是耗时耗力的。MLPs 现在已经成为 CTR 预测问题的流行模型结构。 然而，在互联网规模的用户行为数据丰富的领域，如电子商务行业的在线广告和推荐系统，这些MLPs模型往往缺乏对行为数据具体结构的深入理解和挖掘，为进一步改进留下了空间。

  为了总结阿里巴巴展示广告系统中收集的用户行为数据的结构，我们报告了两个关键观察结果：

• Diversity
  • 用户在访问电子商务网站时对不同种类的商品感兴趣。 例如，一位年轻的妈妈可能同时对 T 恤、皮包、鞋子、耳环、儿童外套等感兴趣。
• Local activation
  • 由于用户兴趣的多样性，每次点击只有一部分用户的历史行为有贡献。 例如，游泳者会点击推荐的护目镜，主要是因为购买了泳衣，而不是她上周购物清单中的书籍。

  在本文中，我们介绍了一种新的模型，称为深度兴趣网络（DIN），该模型是在阿里巴巴的展示广告系统中开发和部署的。受机器翻译模型中使用的注意力机制的启发，DIN 以兴趣分布表示用户的不同兴趣，并设计了一个类似注意力的网络结构，以根据候选广告局部激活相关兴趣。我们在实验部分 6.1 中演示了这种现象。 与候选广告具有更高相关性的行为会获得更高的关注分数并主导预测。在阿里巴巴生产的 CTR 预测数据集上进行的实验证明，在 GAUC(组加权 AUC，见第 3.3 节)度量测量下，所提出的 DIN 模型显着优于 MLP。

  在训练这种大规模稀疏输入的工业深度网络时，很容易遇到过拟合问题。 实验表明，通过添加细粒度的用户行为特征(例如，good-id)，深度网络模型很容易陷入过拟合陷阱并导致模型性能迅速下降。 在本文中，我们仔细研究了这个问题并提出了一种有用的自适应正则化技术，该技术被证明可以有效地提高我们应用中的网络收敛性。

  DIN 在一个名为 X-Deep Learning (XDL) 的多 GPU 分布式训练平台上实现，该平台支持模型并行和数据并行。 利用网络行为的结构属性数据，我们采用共同特征技巧来降低存储和计算成本。 由于 XDL 平台的高性能和灵活性，我们将训练过程加速了大约 10 倍，并以高效率自动优化超参数。

本文的主要贡献如下:

• 我们研究并总结了工业电子商务应用中互联网规模用户行为数据的两个关键结构：多样性和局部激活。
• 我们提出了一个深度兴趣网络(DIN)，它可以更好地捕捉行为数据的具体结构并带来模型性能的提升。
• 我们引入了一种有用的自适应正则化技术来克服在训练具有大规模稀疏输入的工业深度网络中的过拟合问题，这可以很容易地推广到类似的行业任务。
• 我们开发了 XDL，这是一个用于深度网络的多 GPU 分布式训练平台，它具有可扩展性和灵活性，可以支持我们的各种高性能实验。

  在本文中，我们专注于电子商务行业展示广告场景中的点击率预测任务。 这里讨论的方法可以应用于具有丰富互联网规模用户行为数据的类似场景，例如电子商务网站中的个性化推荐、社交网络中的提要排序等。

  本文的其余部分安排如下。 我们在第 2 节讨论相关工作。第 3 节概述了我们的展示广告系统，包括用户行为数据和特征表示。 第 4 节描述了 DIN 模型的设计以及自适应正则化技术。 第 5 节简要介绍了已开发的 XDL 平台。 第 6 节展示了实验和分析。 最后，我们在第 7 节结束本文。

2.相关工作

  CTR预测模型由浅层结构演变为深层结构，特征和样本的规模同时越来越大。 随着特征表示的挖掘，模型结构的设计涉及更多的见解。

  作为一项开创性工作，NNLM(神经网络语言模型) 提出学习单词的分布式表示，旨在避免语言建模中的维度灾难。 这个想法，我们称之为嵌入，启发了许多需要处理大规模稀疏输入的自然语言模型和 CTR 预测模型。

  LS-PLM 和 FM 模型可以看作是一类具有一个隐藏层的网络，它首先在稀疏输入上使用嵌入层，然后对输出施加特殊设计的变换函数，旨在捕捉特征之间的组合关系。

  Deep Crossing、Wide&Deep Learning 和 YouTube Recommendation CTR 模型通过将变换函数替换为复杂的 MLP 网络，扩展了 LS-PLM 和 FM，极大地增强了模型能力。它们遵循类似的模型结构，结合了嵌入层(用于学习稀疏 id 特征的分布式表示)和 MLP(用于自动学习特征的组合关系)。这种CTR预测模型在很大程度上替代了人工人工的特征组合。我们的基础模型遵循这种模型结构。然而，值得一提的是，对于具有用户行为数据的 CTR 预测任务，特征通常包含在多热点稀疏 id中，例如 YouTube 推荐系统中的搜索词和观看的视频。这些模型通常在嵌入层之后添加一个池化层，通过求和或平均等操作来获得固定大小的嵌入向量。这会导致信息丢失，无法充分利用用户丰富的行为数据的内部结构。

  神经机器翻译领域的注意力机制给了我们灵感。NMT 对所有注释进行加权求和以获得预期的注释，并且只关注与双向 RNN 机器翻译任务中下一个目标词的生成相关的信息。这启发了我们设计类似注意力的结构，以更好地模拟用户的历史多样化兴趣。最近的一项工作，DeepIntent 还应用了注意力技术来更好地建模数据的丰富内部结构，它学习将注意力分数分配给不同的单词，以便在赞助搜索中获得更好的句子表示。但是，查询和文档之间没有交互，也就是说，给定模型，查询或文档表示是固定的。这种情况与我们不同，因为在 DIN 模型中，用户表示会随着展示广告系统中的不同候选广告而自适应变化。换句话说，DeepIntent 捕获了数据的多样性结构，但错过了局部激活属性，而提出的 DIN 模型捕获了两者(数据的多样性&局部激活属性)。

3.系统概述

  广告系统的整体场景如图 1 所示。请注意，在电子商务网站中，广告是自然商品。 因此，在没有特别声明的情况下，我们在本文的其余部分将广告称为商品。

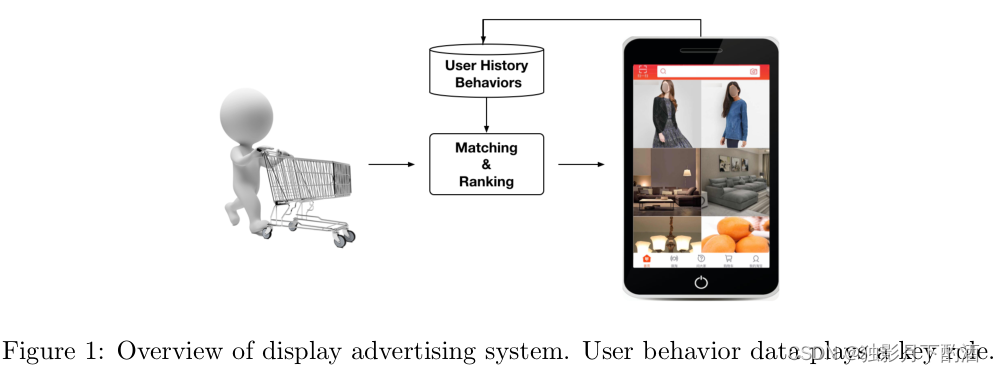
  当用户访问电子商务网站时，系统i) 检查他的历史行为数据ii) 通过匹配模块生成候选广告iii) 预测每个广告的点击概率，并通过排名模块选择合适的可以吸引注意力(点击)的广告iii) 记录给定显示广告的用户反应。这变成了用户行为数据的闭环消费和生成。在阿里巴巴，每天有数亿用户访问电子商务网站，给我们留下大量真实数据。

3.1 用户行为数据的特征

  表 1 显示了从我们的在线产品收集的用户行为示例。 在我们的系统中，用户的行为数据有两个明显的特征：

• Diversity 用户对不同种类的商品感兴趣。
• Local activation 只有一部分用户的历史行为与候选广告相关。

3.2 特征表示

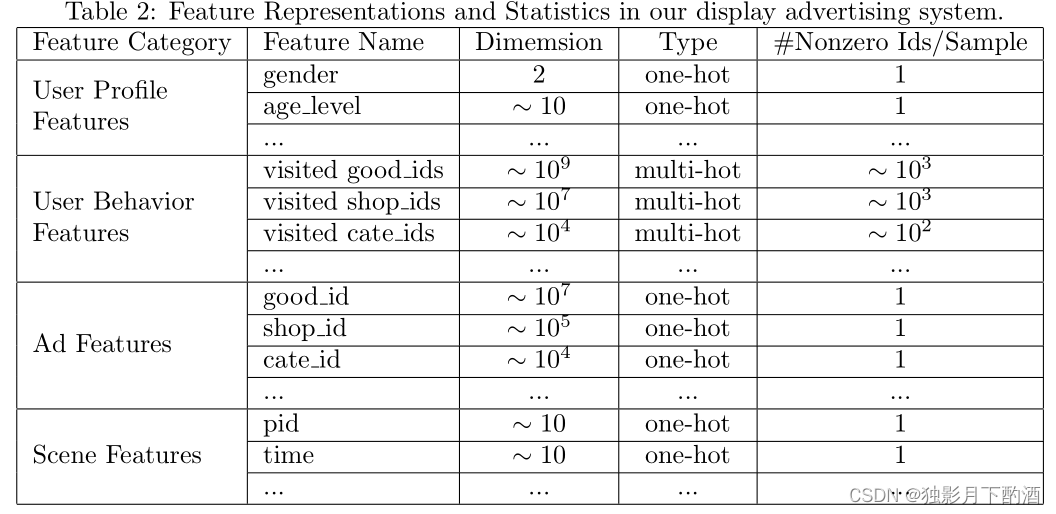
  我们的特征集由稀疏 id 组成，类似于传统的行业设置。 我们将它们分为四组，如表 2 所述。请注意，在我们的设置中没有组合特征。 我们捕捉特征与深度网络的交互。

3.3 评估标准

  接收者操作曲线下面积 (AUC) 是 CTR 预测面积中常用的指标。 在实践中，我们设计了一个 GAUC 的新指标，它是 AUC 的泛化。 GAUC 是每个用户在样本组子集中计算的 AUC 的加权平均值。权重可以是曝光次数或点击次数。 基于曝光的 GAUC 计算如下：
$$GAUC=\frac{{\sum }_{i=1}^n{w}_i\ast AU{C}_i}{{\sum }_{i=1}^n{w}_i}=\frac{{\sum }_{i=1}^{n}impressio{n}_i\ast AU{C}_i}{{\sum }_{i=1}^{n}impressio{n}_i}(1)$$
  GAUC 被实践证明在展示广告场景中更具指示性，其中应用 CTR 模型对每个用户的候选广告进行排名，模型性能主要通过排名列表的好坏来衡量，即用户特定的 AUC。 因此，该方法可以消除用户偏差的影响，更准确地衡量模型对所有用户的性能。 经过多年在我们的生产系统中的应用，GAUC度量被证明比AUC更稳定可靠。

4.模型架构

  与赞助搜索不同的是，大多数用户进入展示广告系统并没有明确的目标。 因此，我们的系统需要一种有效的方法来从丰富的历史行为中提取用户的兴趣，同时构建点击率 (CTR) 预测模型。

4.1基线模型

  遵循流行模型结构，我们的基本模型由两个步骤组成：i) 将每个稀疏 id 特征转移到嵌入式向量空间 ii) 应用 MLP 来拟合输出。 请注意，输入包含用户行为序列 id，其长度可以是各种不同的。 因此，我们添加了一个池化层（eg.求和操作）来处理序列并获得一个固定大小的向量。 如图 2 左侧所示，基本模型在实际中运行良好，现在服务于我们在线展示广告系统的主要流量。

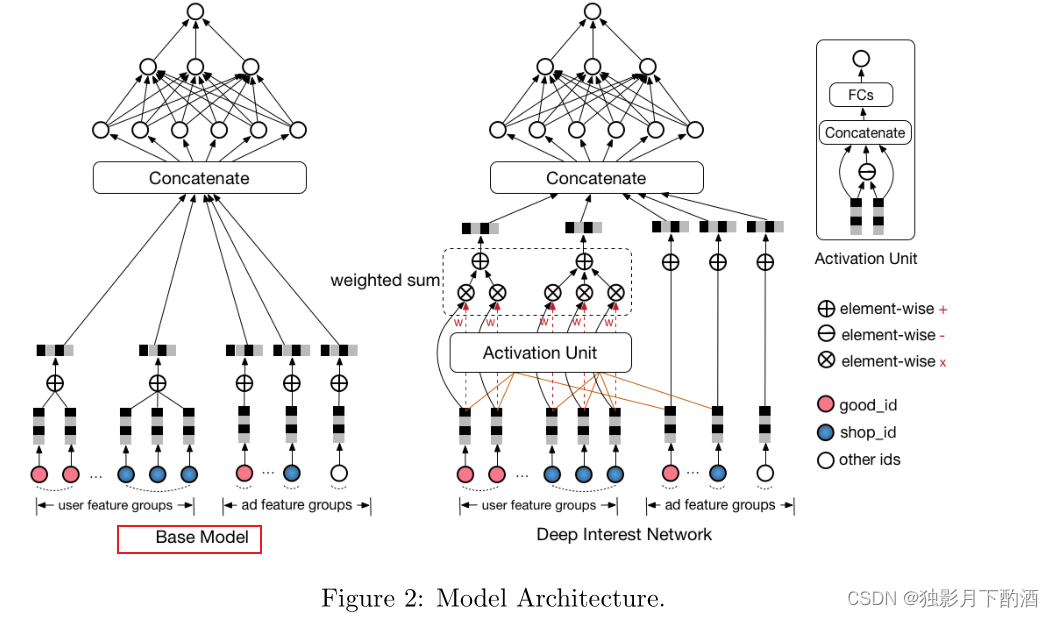
  但是深入池化操作会发现丢失了很多信息，也就是破坏了用户行为数据的内部结构。 这一观察启发我们设计一个更好的模型。

4.2 深度神经网络设计

  在我们的广告场景中，希望模型能够根据用户的历史行为真实地揭示候选广告与用户兴趣之间的关系。

  如上所述，行为数据包含两种结构：多样性和局部激活。 行为数据的多样性反映了用户的各种兴趣。用户对广告的点击往往源于用户的部分兴趣。 我们发现它类似于注意力机制。在 NMT(神经机器翻译) 任务中，假设每个解码过程中每个单词的重要性在句子中是不同的。注意力网络(可以看作是一个特殊设计的池化层)学习为句子中的每个单词分配注意力分数，换句话说，它遵循数据的多样性结构。然而，在我们的应用程序中直接应用注意力层是不合适的，其中用户感兴趣的嵌入向量应该根据不同的候选广告而变化，即它应该遵循局部激活结构。如果不遵循局部激活结构会发生什么。 现在我们得到用户($V_u)$和广告$(V_a)$的分布式表示。对于同一个用户，$V_u$ 是嵌入空间中的一个不动点。广告嵌入 $V_a$ 也是如此。假设我们使用内积来计算用户和广告之间的相关性，$F(U,A)=V_u•V_a$ 。如果 $F(U,A)$ 和 $F(U,B)$ 都很高，这意味着用户 $U$ 与广告 $A$ 和 $B$ 都相关。在这种计算方式下，$V_a$ 和 $V_b$ 的向量连线上的任意一点都会得到很高的相关性分数。 它给用户和广告的分布式表示向量的学习带来了硬约束。可以增加向量空间的嵌入维度来满足约束，这或许可行，但会导致模型参数的巨大增加。

  在本文中，我们介绍了一种新的网络，名为 DIN，它遵循两种数据结构。 DIN 如图 2 的右侧部分所示。从数学上讲，用户 $U$ 的嵌入向量 $V_u$ 变为广告 $A$ 的嵌入向量 $V_a$ 的函数，即：
$$\begin{array}{rl}& V_u=f(V_a)=\sum _{i=1}^N{w}_i\ast V_i=\sum _{i=1}^{N}g(V_i,V_a)\ast V_i(2)\end{array}$$
其中$V_i$表示行为 id $i$ 的embedding向量, 比如good_id、shop_id等。$V_u$ 表示所有行为 id 的加权和。
$w_i$表示行为id $i$ 对候选广告 A 的整体用户兴趣嵌入向量 $V_u$ 贡献的注意力分数。在我们的实现中，$w_i$ 是激活单元（用函数 $g$ 表示）的输出，输入为 $V_i$ 和 $V_a$ 。

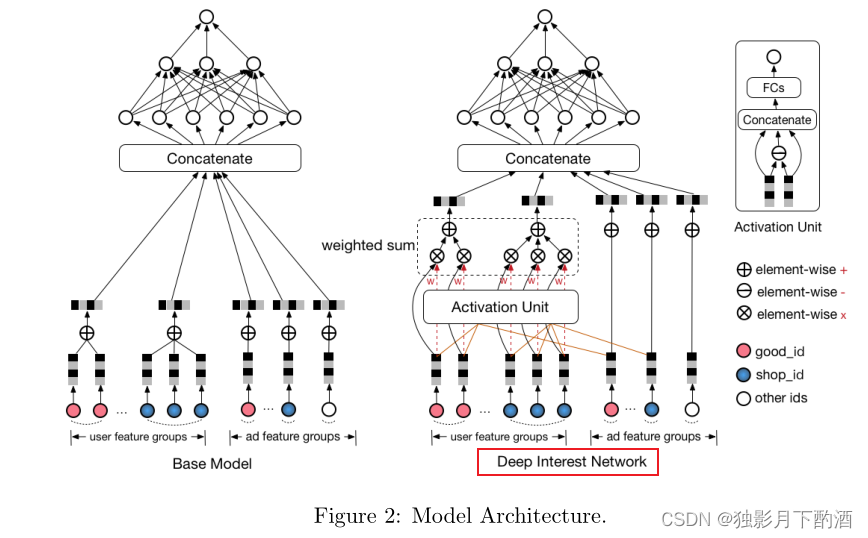
总之，DIN 设计激活单元遵循局部激活结构和加权和池化操作遵循多样性结构。据我们所知，DIN 是第一个在 CTR 预测任务中同时遵循两种用户行为数据结构的模型。

4.3 数据相关激活函数

PReLU 是一种常用的激活函数，在我们一开始的设置中选择，定义为:
$$y_i=\{\begin{array}{l}{y}_i,if{y}_i>0\\ a_i{y}_i,if{y}_i\le 0\end{array}\text{\hspace{1em}(3)}$$
PReLU 扮演 Leaky ReLU 的角色，以避免在 $a_i$ 较小的情况下出现零梯度。先前的研究表明，PReLU 可以提高准确性，但会增加一点过度拟合的风险。

  然而，在我们具有大规模稀疏输入 id 的应用程序中，训练这种工业规模的网络仍然面临很多挑战。为了进一步提高模型的收敛速度和性能，我们考虑并设计了一种新颖的数据相关激活函数，我们将其命名为 Dice：
$$\begin{array}{rl}& y_i=a_i(1-p_i)y_i+y_i{p}_i(4)\\ & p_i=\frac{1}{1+e^{-\frac{y_i-E[y_i]}{\sqrt{Var[y_i]+ϵ}}}}(5)\end{array}$$
训练步骤中的 $E[y_i]$ 和 $Var[y_i]$ 是直接从每个 mini batch 数据中计算出来的，同时我们采用动量法来估计运行中的 $E[y_i{]}^{´}$ 和 $Var[y_i{]}^{´}$：
$$\begin{array}{rl}& {E[y_i{]}_{t+1}}^{´}=E[y_i{]}_t´+\alpha E[y_i{]}_{t+1}(6)\\ & {Var[y_i{]}_{t+1}}^{´}=Var[y_i{]}_t´+\alpha Var[y_i{]}_{t+1}(7)\end{array}$$
其中 $t$ 是训练过程的小批量步数，$\alpha$ 是像 0.99 这样的超参数，在测试步数中，我们使用了运行的 $E[y_i{]}^{´}$ 和 $Var[y_i{]}^{´}$

  Dice 的关键思想是根据数据自适应调整整流器点，这与使用基于 yi>0 的硬整流器的 PReLU 不同。这样，Dice 可以看作是一个有两个通道的软整流器：$a_i{y}_i$ 和基于 $p_i$ 的 $y_i$。$p_i$ 是保持原始 $y_i$ 的权重，当 $y_i$ 偏离每个 mini batch 数据的 $E[y_i]$ 时，它会更低。实验表明，Dice 对收敛速度和 GAUC 有明显的改进。

4.4 自适应正则化技术

  毫不奇怪，在使用大规模参数和稀疏输入训练我们的模型时会遇到过拟合问题。我们通过实验证明，通过添加细粒度的用户访问good_ids 特征，模型性能在第一个 epoch 之后迅速下降。

  防止模型过拟合的方法很多，例如 L2 和 L1 正则化以及 Dropout。然而，对于稀疏和高维数据，点击率预测任务面临更大的挑战。众所周知，互联网规模的用户行为数据遵循长尾定律，即大量特征ids在训练样本中出现几次，而很少出现多次。这不可避免地会在训练过程中引入噪声并加剧过拟合。

  减少过拟合的一个简单方法是过滤掉那些低频特征 id，可以看作是手动正则化。然而，这种基于频率的滤波器在信息丢失和阈值设置方面相当粗糙。在这里，我们介绍了一种自适应正则化方法，其中我们根据特征 id 的出现频率对其施加不同的正则化强度。
$$I_i=\{\begin{array}{l}1,\exists (x_j,y_j)\in B.s.t.[x_j{]}_i\ne 0\\ 0,otherwises\end{array}\text{\hspace{1em}(8)}$$
  更新公式如式（9）所示。 $B$ 代表大小为 $b$ 的小批量样本。 n${}_i$ 是特征 $i$ 的频率，$\lambda$ 是正则化参数。
$$\begin{array}{r}{w}_i\leftarrow w_i-\eta [\frac{1}{b}\sum _{(x_i,y_i)\in B}\frac{\partial L(f(x_j),y_j)}{\partial w_i}+\lambda \frac{1}{n_i}{w}_i{I}_i]\end{array}\text{\hspace{1em}(9)}$$
等式（9）背后的思想是惩罚低频特征并放松高频特征以控制梯度更新方差。

  自适应正则化的类似做法可以在 [17](Mu Li.et.al) 中找到，它将正则系数设置为与特征频率成正比，如下所示：
$$\begin{array}{r}{w}_i\leftarrow w_i-\eta [\frac{1}{b}\sum _{(x_i,y_i)\in B}\frac{\partial L(f(x_j),y_j)}{\partial w_i}+\lambda n_i{w}_i{I}_i]\end{array}\text{\hspace{1em}(10)}$$
  然而，在我们的数据集中，使用 Eq.(10) 的正则化训练没有明显缓解过拟合。 相反，它减慢了训练过程的收敛速度。 等式(10)对高频的good id比长尾的好，而前者在电子商务系统中对度量和在线收入的贡献更大。 此外，我们还评估了 dropout 技术，发现对过拟合有轻微的改进。

5.实现

  DIN 在一个名为 X-Deep Learning (XDL) 的多 GPU 分布式训练平台上实现，该平台支持模型并行和数据并行。 XDL 旨在解决训练具有大规模备用输入和数百亿参数的工业规模深度学习网络的挑战。 在我们的观察中，现在发布的大多数深度网络都是通过两个步骤构建的：i) 采用嵌入技术将原始稀疏输入转换为低维密集向量 ii) 与 MLP、RNN、CNN 等网络进行桥接。大多数参数都集中在第一个嵌入步骤中，该步骤需要分布在多台机器上。 第二个网络步骤可以在单机内处理。在这样的思想下，我们以桥接方式构建XDL平台，如图3所示，由三种主要组件组成：

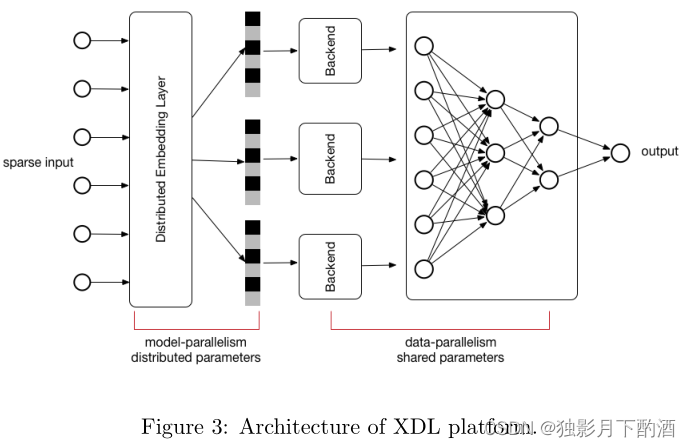
• Distributed Embedding Layer
  • 它是一个模型并行模块，嵌入层的参数分布在多个 GPU 上。 嵌入层作为预定义的网络单元工作，提供前向和后向模式。
• Local Backend
  • 它是一个独立的模块，旨在处理本地网络训练。 这里我们用了开源的深度学习框架，如tensorflow、mxnet、theano等。通过统一的数据交换接口和抽象，我们很容易在不同类型的框架中集成和切换。 后端架构的另一个好处是可以方便地轻松跟进开源社区，并利用这些开源深度学习框架开发的最新发布的网络结构或更新算法。
• Communication Component
  • 它是基本模块，有助于并行嵌入层和后端。 在我们的第一个版本中，它是用 MPI 实现的。

  此外，关于数据的结构属性，我们还采用了共同特征技巧[8]。 读者可以在[8]中找到详细的介绍。

[8] Learning piece-wise linear models from large scale data for ad click prediction

  由于 XDL 平台的高性能和灵活性，我们将训练过程加速了大约 10 倍，并以高调优效率自动优化超参数。

6.实验

6.1可视化DIN

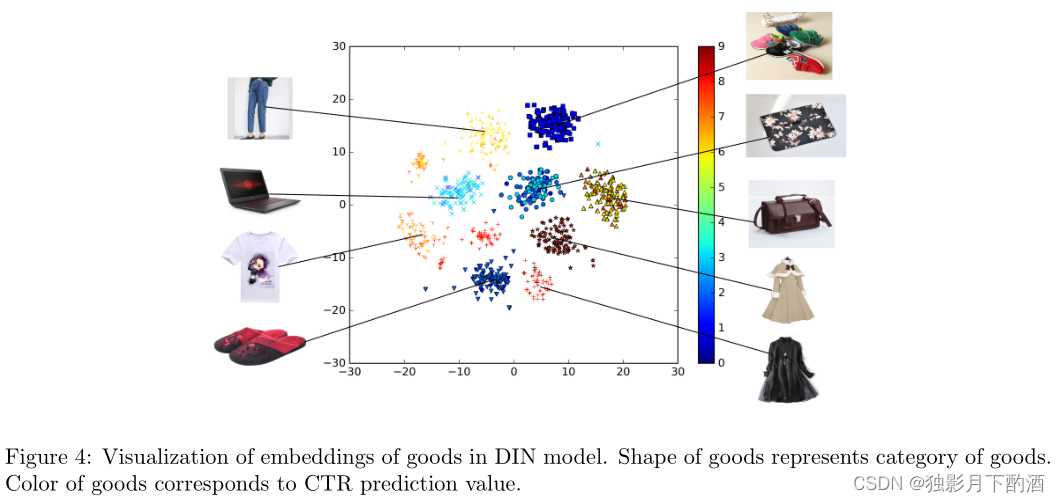
  在 DIN 模型中，稀疏的 id 特征被编码为嵌入向量。 在这里，我们随机选择了 9 个类别(连衣裙、运动鞋、包包等)和每个类别的 100 件商品。 图 4 展示了基于 t-SNE 的商品嵌入向量的可视化，其中形状相同的点对应相同的类别。 它清楚地显示了 DIN 嵌入的聚类特性。

  此外，我们以预测方式对图 4 中的点进行着色：假设所有商品都是年轻母亲的候选商品(表 1 中的示例)，它们按预测值着色(红色的 CTR 比蓝色的高)。 DIN模型正确识别满足用户多样化兴趣的商品。

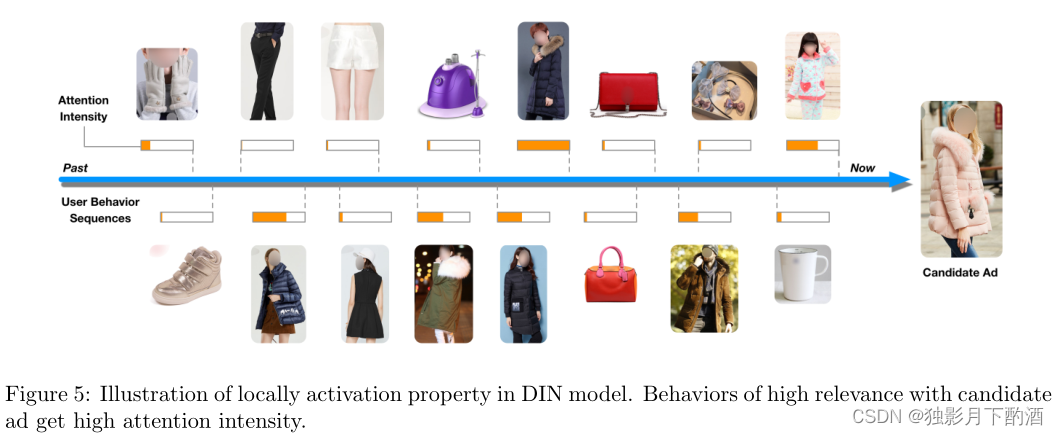
  此外，我们深入研究 DIN 模型以检查工作机制。 如第 4.2 节所述，DIN 设计注意单元以局部激活与候选广告相关的行为。 图 5 说明了激活强度(注意力分数 $w$)。 正如预期的那样，与候选广告高度相关的行为会得到高度关注。

6.2 正则化

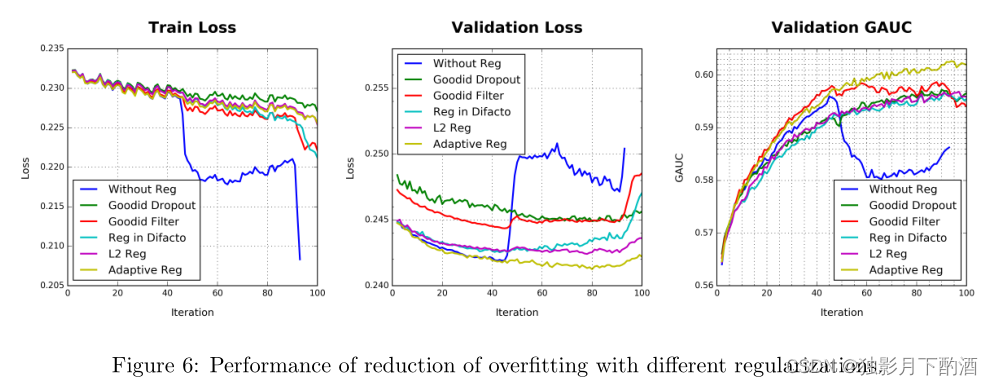
  基线模型和我们提出的 DIN 模型在训练过程中都遇到过拟合问题，并添加了细粒度特征，例如 good_id 特征。 图 6 说明了有/没有细粒度 good_id 特征的训练过程，清楚地说明了过拟合问题。

我们现在通过实验比较不同类型的正则化。

• Dropout 随机丢弃每个样本中 50% 的 good_id。
• Filter 按样本中的出现频率过滤good id，只留下最频繁的good id。 在我们的设置中，剩下前 2000 万个good的 ID。
• L2 regularization 参数λ并设置为0.01。
• Regularization in DiFacto DiFacto 提出了 Eq.(10) 的这种方法。 参数λ并设置为0.01。
• Adaptive regularization 我们提出的方程式方 (9)。 我们使用 Adam 作为优化方法。 参数 $\lambda$ 并设置为0.01。

  比较结果如图6所示。验证结果证明了我们提出的自适应正则化方法的有效性。 使用自适应正则化技术进行训练，具有细粒度good_id 特征的模型与没有它的模型相比，在 GAUC 上实现了 0.7% 的增益，这是 CTR 预测任务的显着改进。

  Dropout 方法导致第一个 epoch 的收敛速度较慢，而在第一个 epoch 完成后，过拟合得到了一定程度的缓解。 频率滤波器在第一个epoch保持与无操作设置相同的收敛速度。 在第一个 epoch 之后，过拟合也得到了缓解，但仍然比 dropout 设置差。 在自适应正则化设置中，我们几乎看不到第一个 epoch 之后的过度拟合。 当第二个 epoch 完成时，验证集上的损失和 GAUC 几乎收敛。

  Eq.(10) 的 DiFacto [17] 中的正则化对高频的 good id 设置了更大的惩罚。 然而，在我们的任务中，高频的good id 更自信地刻画了用户的兴趣，而低频good id 会带来很多噪声。 频率滤波器的实验可以说明这一点。 我们的方法通过应用商品频率的常规倒数来软化低频商品 ID。

6.3 DIN与基线模型比较

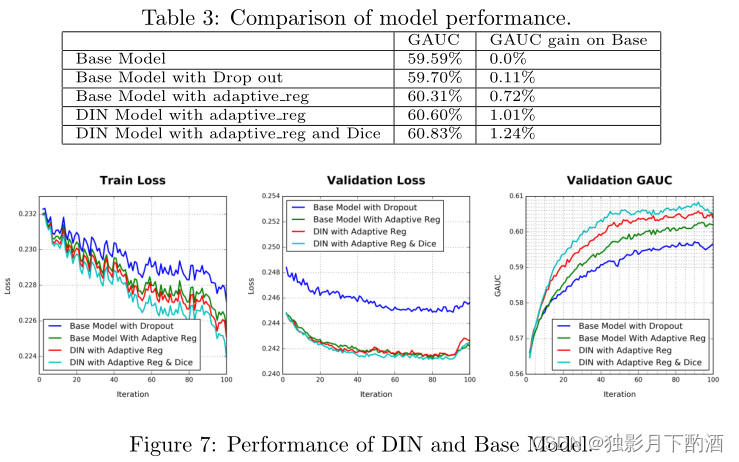
  在阿里巴巴的生产性展示广告系统上测试模型性能。 训练和测试数据集都是从系统日志生成的，包括曝光和点击日志。 我们收集两周的训练样本和第二天的测试样本，这是我们系统中的一个高效设置。 基本模型和我们提出的 DIN 模型都是在表 3.2 中描述的相同特征表示上构建的。 参数单独调整，报告最佳结果。 GAUC 用于评估模型性能。

  结果如表 3 和图 7 所示。显然，使用自适应正则化训练的 DIN 模型明显优于基础模型。 具有自适应 reg 的 DIN 仅使用基本模型的一半迭代来获得基本模型的最高 GAUC。 最终它比基础模型实现了 1.08% 的 GAUC 增益，这对我们的生产系统来说是一个很大的改进。 与 DIN 相比，Dice 获得了 0.23% 的 GAUC 增益。 随着对用户行为数据结构的更好理解和利用，DIN模型表现出更好的捕捉用户和候选广告非线性关系的能力。

7.结论

  在本文中，我们专注于电子商务行业展示广告场景下的CTR预测任务，其中涉及互联网规模的用户行为数据。 我们揭示和总结了数据的两个关键结构：多样性和局部激活，并设计了一个名为 DIN 的新模型，更好地利用了数据结构。 实验表明，与流行的 MLPs 模型相比，DIN 带来了更多的可解释性并实现了更好的 GAUC 性能。 此外，我们研究了在训练此类工业深度网络中的过拟合问题，并提出了一种自适应正则化技术，可以在我们的场景中大大减少过拟合。 我们认为这两种方法可能对其他工业深度学习任务具有指导意义。

  与图像识别和自然语言处理领域具有成熟和最先进的深度网络结构不同，具有丰富互联网规模用户行为数据的应用仍然面临着许多挑战，值得付出更多努力。 研究和设计更常见和有用的网络结构。 我们将继续关注这个方向。