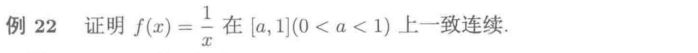目录
利用单调有界原理求数列收敛,主要分为两步
利用切线放缩和定积分放缩
拆成两个调和级数相减+拉链定理
使用诱导公式转化为可以使用等价无穷小的情形
无穷区间零点定理的取点
证明数列收敛有四种方法
证明调和级数发散的方法
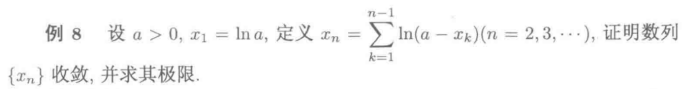
利用单调有界原理求数列收敛,主要分为两步
- 使用数学归纳法证明数列有界
- 通过作差或作商比较,证明数列是单调的
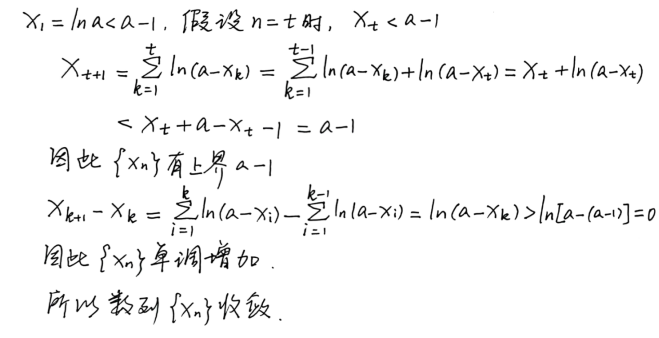
至于书上的解答,实际上是把证明有界和证明单调的过程混在一起了,做法很巧妙,但是有一点点乱,个人感觉不如分开,分别证明
求极限的过程略去
![]()
这个收敛的值显然就是欧拉常数C
证明单调较为简单,证明有界时需要放缩。这里给出两种解答,分别
利用切线放缩和定积分放缩
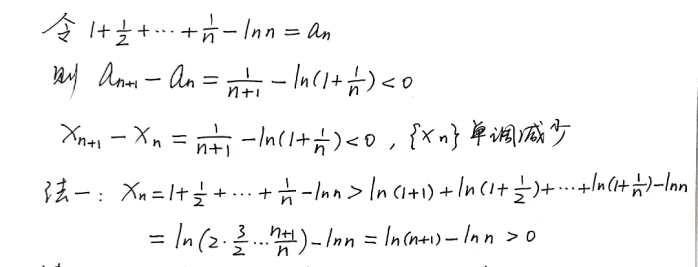
以上是利用了切线放缩。下面来看看利用定积分放缩
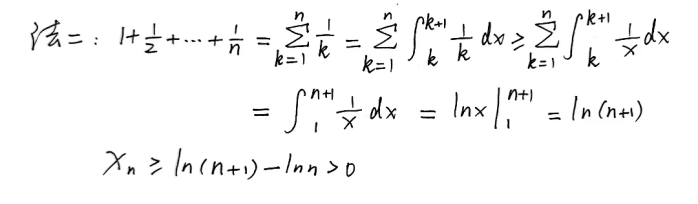
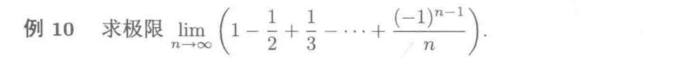
拆成两个调和级数相减+拉链定理
基本思路是拆成两个调和级数相减,再用欧拉常数即可
但是要注意的是,这里需要分奇偶讨论,然后再用拉链定理证明原式极限存在
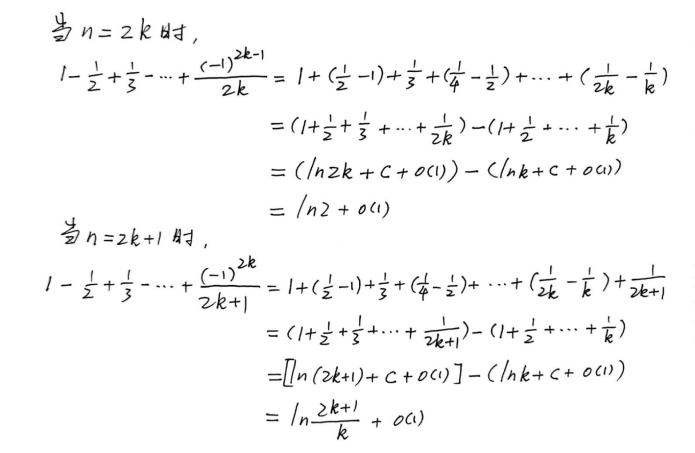
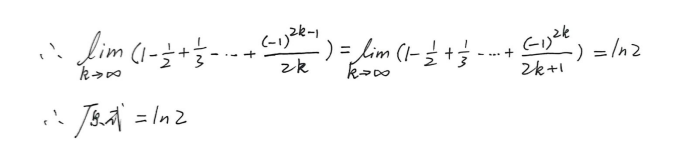
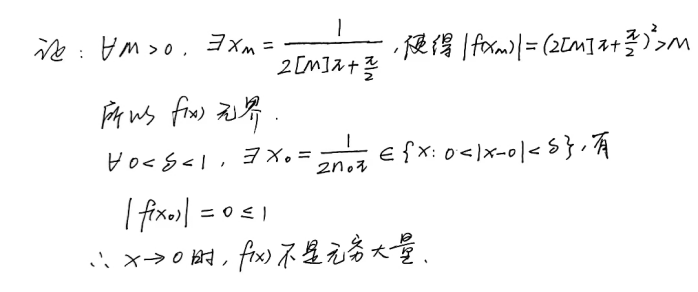
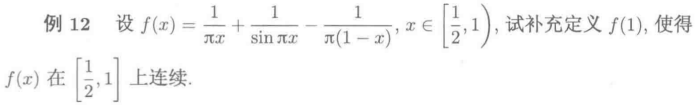
使用诱导公式转化为可以使用等价无穷小的情形
这个题如果直接使用等价无穷小时会遇到问题,sin()括号中的是趋于π的。但事实上只需要简单转化以下,因为互补的角正弦值是相等的
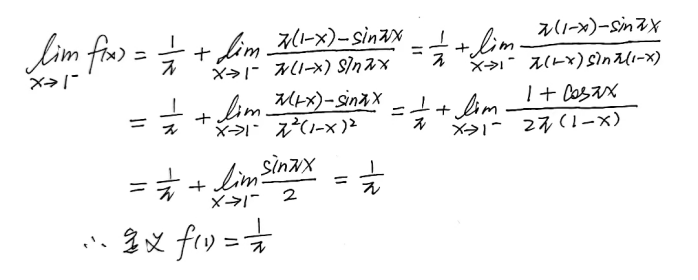

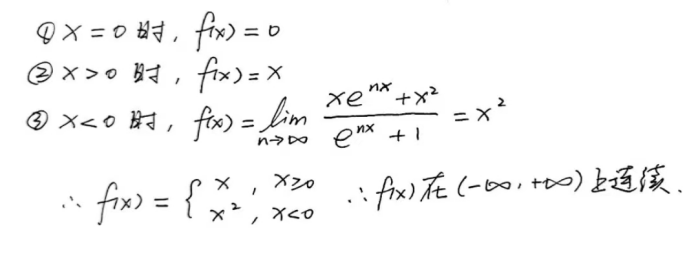
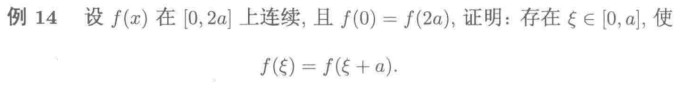
张天德常考题型中有十分相近的原题,做法也如出一辙
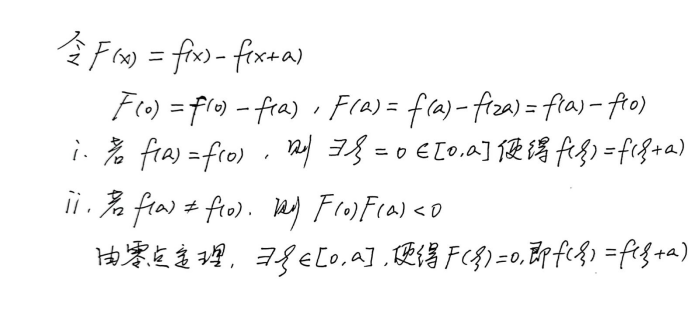
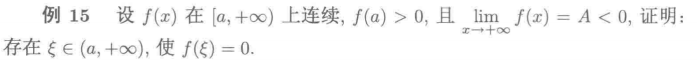
无穷区间零点定理的取点
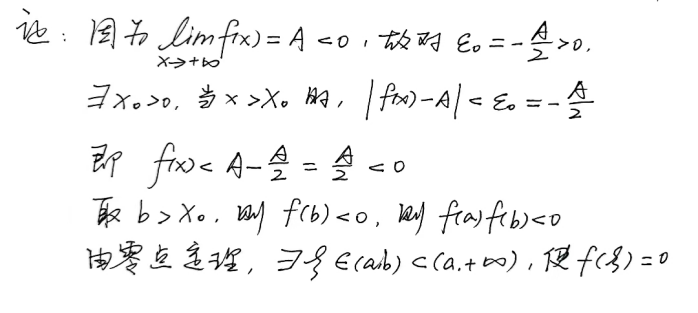
![]()
如何求解该题目?
证明数列收敛有四种方法
- 极限的定义 需要知道收敛到何值
- 单调有界准则 抽象数列,或容易判断单调性和上下界
- 夹逼准则 尤其使用含有阶乘项的;放缩后两端的极限要存在且相等
- 柯西收敛原理 不知道具体极限,不单调,也无法使用夹逼准则的
具体该用哪一个呢?首先,由于不知道该数列具体收敛于哪个值,所以定义法不做考虑。由于每一项有正有负,显然不单调,也不能用单调有界准则。能不能用夹逼准则?貌似也不太行,如果按照简单的|sinx|小于等于1来放缩,左右两端的极限不相等。于是我们采用柯西收敛准则
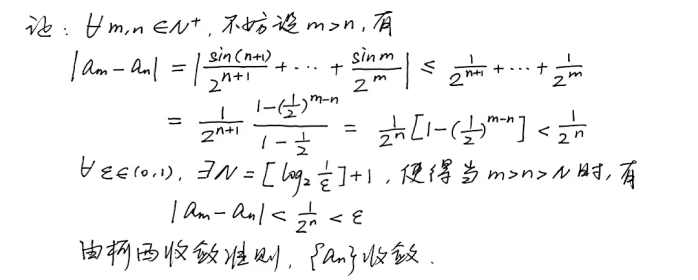
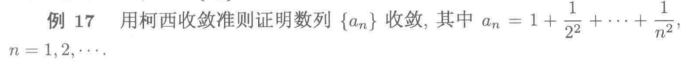
本题虽然指定了证明方法,在这里也用单调有界原理证明一下
其单调递增是显然的,现证明其有上界
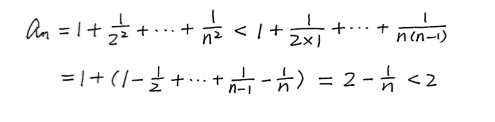
下面用柯西收敛原理来证明

![]()
证明调和级数发散的方法
这里只列举部分
- 伯努利兄弟的证法
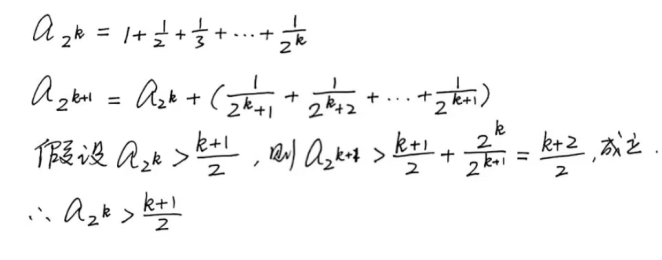
- lnx的切线放缩
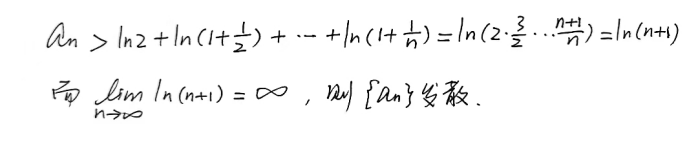
- 柯西收敛准则的否定叙述
这也是本书中的做法
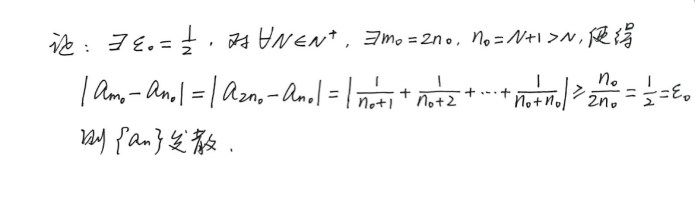

证明此题需要用到海涅定理


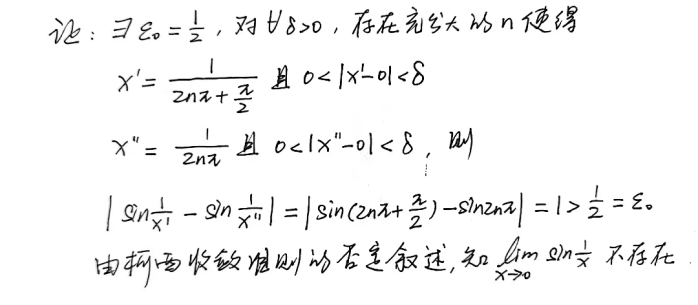

这道题较为繁琐了