文章目录
- 1. 冒泡排序
- 2. 插入排序
- 3. 希尔排序
- 4. 选择排序
- 5. 堆排序
- 6. 快速排序
- 7. 归并排序
1. 冒泡排序
从 0 号下标开始遍历,相邻两个数相互比较,如果左边的数大于右边的数,执行交换操作,最终每一趟冒泡都会将一个最大的数移到最右边
public class Main {
public static void sort(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
// 外层循环记录比较次数,n 个数只需要比较 n - 1 此即可
for (int i = 0; i < nums.length - 1; i++) {
// 每次冒泡都会将一个最大的数移到最后,下一次冒泡不需要再遍历它,所以 -i
for (int j = 0; j < nums.length - 1 - i; j++) {
if (nums[j] > nums[j + 1]) {
// 如果左边的大于右边的,进行交换
swap(nums, j, j + 1);
}
}
}
}
public static void swap(int[] nums, int a, int b) {
int tmp = nums[a];
nums[a] = nums[b];
nums[b] = tmp;
}
}
2. 插入排序
一次插入排序的过程大致如下:
-
将整个区间分成一个无序区间和一个有序区间,有序区间为 [0, i],无序区间为 [i + 1, n)
-
取出无序区间的第一个元素记为 k,反向遍历有序区间,将遍历到的每个元素跟 k 进行比较,当遍历到的元素大于 k 时,就将此元素后移一位
-
当遍历到有序区间的某个元素小于 k 时,说明前面的所有数小于 k,将 k 放入此元素的后一个位置即可,至此一次插排结束
public void insertSort(int[] nums) {
for (int i = 0; i < nums.length - 1; i++) {
// 外层循环记录插排的次数
// 取出无序区间的第一个元素
int k = nums[i + 1];
int j;
for (j = i; j >= 0; j--) {
// 内层循环反向遍历无序区间,跟 k 进行比较
if (nums[j] <= k) {
// 遍历到的元素 <= k,说明前面的元素都 <= k,直接跳出循环
break;
}
// 遍历到的元素 > k,将此元素位置后移一位
nums[j + 1] = nums[j];
}
// 将 k 值放在比它大的元素后一个位置
nums[j + 1] = k;
}
}
3. 希尔排序
希尔排序可以认为是一种特殊的插入排序,一种在逻辑上设置间隔分组的插入排序
将序列内每相隔 gap 各单位的数认为是一组,然后在组内进行插入排序
gap 的初始值设置为数组长度的一半,每进行一次希尔排序,gap 变为原来的一半
当 gap 等于 1 时,就可以认为本次希尔排序是插入排序

public void shellSort(int[] nums) {
// 定义间隔 gap
int gap = nums.length / 2;
// 循环开始进行排序
while (gap >= 1) {
for (int i = 0; i < nums.length - gap; i++) {
// 取出无序数组第一个元素
// 组内元素之间是有间隔存在的,所以取无序区间的第一个元素时需要加上间隔值 gap
int k = nums[i + gap];
int j;
// 循环遍历本组的有序区间,并且将遍历到的元素跟 k 比较
for (j = i; j >= 0; j -= gap) {
if (nums[j] <= k) {
break;
}
// 当遍历到的元素大于 k,就将此元素位置后移 gap 位
nums[j + gap] = nums[j];
}
// 将 k 值放在比它大的元素后 gap 位
nums[j + gap] = k;
}
// 每进行完一次希尔排序,就将 gap 变为原来的一半
gap /= 2;
}
}
4. 选择排序
将整个序列在逻辑上分成有序区间和无序区间,有序区间在前,无序区间在后
每一次选择排序都会将无序区间中最大的元素放到无需区间的最后一位,然后在逻辑上将无序区间的最后一位规划给有序区间
因为每次在无序区间中选出的都是最大的元素,所以可以保证后面有序区间必然有序
在第一次选择排序之前,有序区间是不存在的,整个序列都是无序序列
public void selectSort(int[] nums) {
// 外层循环控制进行选择排序的次数
for (int i = 0; i < nums.length - 1; i++) {
int maxIndex = 0; // 假设无需区间的最大元素在第一位
// 遍历无序区间,找到最大的元素,将最大元素的下标赋给 maxIndex
for (int j = 1; j < nums.length - i; j++) {
if (nums[j] > nums[maxIndex]) {
maxIndex = j;
}
}
// 交换最大元素和无序区间的最后一个元素
swap(nums, maxIndex, nums.length - 1 - i);
}
}
private void swap(int[] nums, int a, int b) {
int tmp = nums[a];
nums[a] = nums[b];
nums[b] = tmp;
}
}
5. 堆排序
堆排序可以说是一种特殊的选择排序
同选择排序一样,将整个序列分为有序区间和无序区间,再将无序区间的最大值(或最小值)放到无序区间的最后,再在逻辑上把这个元素规划给有序区间
不同的是,堆排序中以堆的性质来要求无序区间,使得无序区间的第一个元素永远是最大(或最小)的
也就是把在选择排序中循环寻找最大值的操作替换成了堆中的向下调整的操作,向下调整可以使得堆顶元素保持最大(或最小)
向下调整的步骤:
- 判断当前节点是不是叶子节点,如果是叶子节点,直接退出,如果不是,继续下面步骤
- 找到当前节点左右孩子的最大值
- 如果小于,说明符合大根堆的性质,退出即可
- 如果最大值大于当前节点就交换当前节点的值和最大值
- 如果发生了交换,很有可能破坏了下面节点的大根堆性质,则继续对下面节点进行向下调整
public void heapSort(long[] nums) {
// 建立大根堆
// 当前例子进行递增排序,如果需要进行递减排序,则需要建立小根堆
createBigHeap(nums);
// 控制交换次数
for (int i = 0; i < nums.length - 1; i++) {
// 交换无序区间第一个元素和最后一个元素
swap(nums, 0, nums.length - 1 - i);
// 交换完成之后进行向下调整,使得数组符合大根堆的性质
// 逻辑上交换完成之后无序区间的最后一个元素已经属于有序区间,所以进行向下调整的堆的 size 应该减去已经进入有序区间的元素的个数
shiftDown(nums, nums.length - 1 - i, 0);
}
}
// 建堆就是对数组从最后一个非叶子节点下标处开始向前循环进行向下调整的操作
private void createBigHeap(long[] nums) {
for (int i = (nums.length - 2) / 2; i >= 0; i--) {
shiftDown(nums, nums.length, i);
}
}
private void shiftDown(long[] nums, int size, int index) {
// 当当前节点的下标大于或等于 size 时,说明当前节点是叶子节点
while (2 * index + 1 < size) {
int maxIndex = 2 * index + 1; // 假设当前节点左孩子为最大值
int right = maxIndex + 1;
// 如果右孩子存在且右孩子的值大于左孩子的值,将右孩子的值赋给最大值
if (right < size && nums[right] > nums[maxIndex]) {
maxIndex = right;
}
// 如果当前节点的值大于等于最大值,说明符合大根堆,直接 return
if (nums[index] >= nums[maxIndex]) {
return;
}
// 如果不满足大根堆,就交换当前节点的值和最大值
swap(nums, index, maxIndex);
// 将最大值下标赋给 index,继续循环进行向下调整
index = maxIndex;
}
}
private void swap(long[] nums, int a, int b) {
long tmp = nums[a];
nums[a] = nums[b];
nums[b] = tmp;
}
6. 快速排序
大致流程:
- 选择一个元素作为基准值(pivot),一般选择最右边或最左边的元素,通过遍历的方式,比较 pivot 和区间内其他元素的大小关系
- 在遍历期间,通过算法的设计,保证如下图所示的区间内位置关系,此时 pivot 就位于当区间有序时它该处于的位置
- 继续对左右两个小区间按照同样的方式进行处理

在元素遍历过程中,引入几个边界值,来保证下图所示的区间位置关系

public void quickSort(long[] nums) {
quickSortRange(nums, 0, nums.length - 1);
}
private void quickSortRange(long[] nums, int from, int to) {
// 当待比较区间中只有一个或没有元素时,说明比较结束
if (to - from + 1 <= 1) {
return;
}
// 对待比较区间中的元素做 partition
// 将大于基准值(pivot)的元素放在 pivot 前面,小于 pivot 的元素放在 pivot 后面
// 最终得到 pivot 有序时应该存在于区间中的下标
int pi = partition(nums, from, to);
// 对 pivot 左边的元素递归排序
quickSortRange(nums, from, pi - 1);
// 对 pivot 右边的元素递归排序
quickSortRange(nums, pi + 1, to);
}
private int partition(long[] nums, int from, int to) {
// 定义 left 和 right,确定待比较区间的左右边界下标
int left = from;
int right = to;
// 定义 pivot 值,一般定义为区间最右边的值
long pivot = nums[to];
// 只要待比较区间中还有元素,就继续循环
while (left < right) {
// 循环比较,当左边的元素小于 pivot 时,left 下标就右移,大于时跳出循环
// 加上 left < right 条件是因为,left 在循环 ++ 的时候,很有可能跳出边界值,所以在每次比较之前先保证 left 值合法
while (left < right && nums[left] <= pivot) {
left++;
}
// 循环比较,当右边的元素大于 pivot 时,right 下标就左移,小于时跳出循环
// 加上 left < right 条件是因为,right 在循环 -- 的时候,很有可能跳出边界值,所以在每次比较之前先保证 right 值合法
while (left < right && nums[right] >= pivot) {
right--;
}
// 上面两次循环都跳出之后,说明当前 right 下标处元素小于 pivot,left 下标处元素大于 pivot,交换两元素位置
swap(nums, left, right);
}
// 当待比较区间没有元素时,将 pivot 和当前 left 下标处的元素交换位置
swap(nums, left, to);
// 返回 pivot 下标
return left;
}
private void swap(long[] nums, int a, int b) {
long tmp = nums[a];
nums[a] = nums[b];
nums[b] = tmp;
}
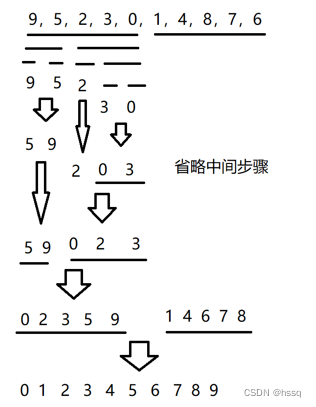
7. 归并排序
基本思路: 归并排序就是将区间分成一个个小区间分别进行排序,在对小区间进行合并得到最终有序的大区间。基本步骤如下图:
public void mergeSort(long[] nums) {
mergeSortRange(nums, 0, nums.length);
}
private void mergeSortRange(long[] nums, int from, int to) {
// 计算当前区间元素数量
int size = to - from;
// 找到当前区间中间下标
int mid = from + size / 2;
// 当前区间中元素个数 <= 1 时,说明此区间排序完成
if (size <= 1) {
return;
}
// 对左边小区间进行递归排序
mergeSortRange(nums, from, mid);
// 对右边小区间进行递归排序
mergeSortRange(nums, mid, to);
// 合并有序数组
merge(nums, from, mid, to);
}
private void merge(long[] nums, int from, int mid, int to) {
// 计算合并后总共需要的数组大小
int size = to - from;
// 初始化一个数组,用来存放排好序的元素
long[] array = new long[size];
// 左边小区间的下标
int left = from;
// 右边小区间的下标
int right = mid;
// 存放有序序列的数组下标
int dest = 0;
// 左右两个区间中还有元素,就继续进行比较
while (left < mid && right < to) {
if (nums[left] <= nums[right]) {
// 左边区间元素更小,放入临时数组
array[dest++] = nums[left++];
} else {
// 右边区间元素更小,放入临时数组
array[dest++] = nums[right++];
}
}
// 当有一个区间的元素取完之后,另一个区间的元素还有可能没有取完,全部放入
// 下面两个循环肯定只会执行一个
while (left < mid) {
array[dest++] = nums[left++];
}
while (right < to) {
array[dest++] = nums[right++];
}
// 将临时数组的元素放入原始数组中
for (int i = 0; i < size; i++) {
nums[from + i] = array[i];
}
}