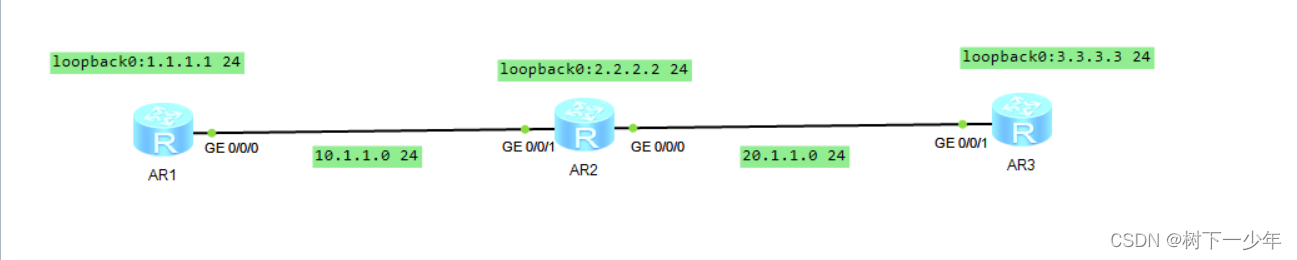
学习目标:
学习定积分的换元积分法和分部积分法,我会采取以下步骤:
-
熟悉基本概念和公式:首先,要对定积分、换元积分法和分部积分法有基本的理解,并掌握它们的基本公式和性质。
-
学习经典例题:找一些经典的例题,理解它们的解题思路,注意其中的技巧和要点,掌握其中的方法和步骤。
-
多做练习题:练习是巩固知识的关键。选择适当难度的练习题,不断地进行练习和实践,提高自己的解题能力和熟练度。
-
理解应用场景:在学习过程中,应该注意定积分、换元积分法和分部积分法的应用场景,理解它们在实际问题中的作用和意义。
-
注重细节和常见错误:在学习过程中,需要特别注重细节和常见错误,注意细节处理,避免犯常见的错误,提高解题的准确性和有效性。
-
请教老师和同学:在学习过程中,如果遇到问题或不理解的地方,可以向老师或同学请教,及时解决问题,提高学习效率。





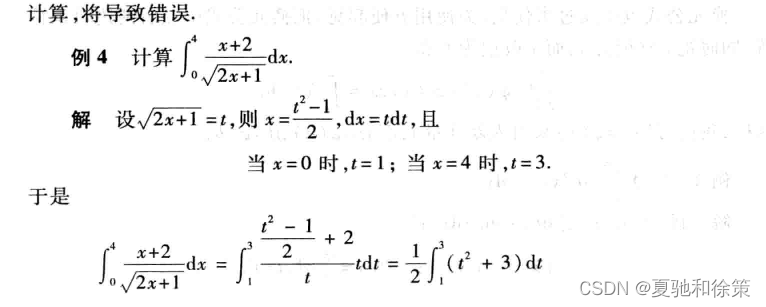





 我的理解:
我的理解:
定积分的换元积分法,也称为定积分的代换法,是利用换元公式对定积分进行求解的方法。
具体而言,定积分的换元积分法包括以下步骤:
-
选择适当的代换变量:选择一个新的自变量,令其等于原来的自变量经过一个函数变换后的结果。
-
计算新的积分上下限:将原积分上下限带入代换变量中,得到新的积分上下限。
-
求解新的被积函数:将原函数用代换变量表示,并对其进行求导和化简,得到新的被积函数。
-
用新的被积函数求解定积分:将新的被积函数代入积分公式中,求解新的积分。
-
将代换变量换回原来的自变量:将代换变量用原来的自变量表示,得到最终的积分解。
需要注意的是,选择适当的代换变量是定积分的换元积分法的重点和难点,需要根据具体问题的特点和要求进行选择。此外,还需要注意积分上下限的变换和新的被积函数的求解过程中的代数化简和计算技巧,避免出现计算错误和漏项。
定积分和不定积分的换元积分法的异同:
定积分的换元积分法和不定积分的换元积分法在基本思路上是相同的,都是利用代换公式对积分式进行变形求解。但是,两者在具体的计算方法上存在一些异同:
-
代换变量的选择不同:对于不定积分的换元积分法,一般选择一个新的自变量,令其等于原来的自变量经过一个函数变换后的结果。而对于定积分的换元积分法,除了代换自变量之外,还需要对积分上下限进行相应的变换。
-
积分公式的使用不同:在不定积分的换元积分法中,通常需要将被积函数和其导数的乘积用积分公式进行转化。而在定积分的换元积分法中,需要根据积分上下限的变换情况,选择合适的积分公式进行求解。
-
计算步骤的不同:不定积分的换元积分法通常包括选取代换变量、计算新的被积函数、对新的被积函数进行积分等步骤。而定积分的换元积分法则需要在计算新的被积函数的同时,对积分上下限进行相应的变换,最后才能利用积分公式进行求解。
因此,在学习和应用换元积分法时,需要注意对两者的异同进行理解和区分,根据具体情况选择适当的方法进行求解。

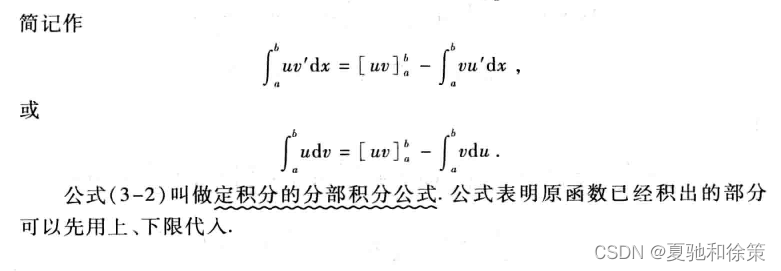



定积分的分部积分法是指利用不定积分的分部积分法,求解定积分的方法。其基本思想是将被积函数表示成两个函数相乘的形式,然后再对其中一个函数积分,对另一个函数求导。具体步骤如下:
-
将被积函数表示成两个函数相乘的形式,即
-
对求导,对 积分,即 和 。
-
将步骤2中求导和积分得到的表达式代入积分式中,得到
-
对得到的积分式不断应用分部积分法,直到能够求得积分或者无法再应用分部积分法为止。
分部积分法对于一些具有一定规律的积分可以起到很好的作用,但是也存在一些难点和易错点:
- 需要选择合适的,通常选择较为困难。
- 分部积分法通常需要多次应用,容易出错。
- 需要注意积分的边界条件,否则会出现漏解或重复解的情况。
因此,在应用分部积分法时,需要仔细选择,注意积分的边界条件,以避免出现错误。