[洛谷-P2585][ZJOI2006]三色二叉树(树形DP+状态机DP)
- 一、题目
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 数据规模与约定
- 二、分析
- 1、递归建树
- 2、树形DP + 状态机DP
- (1)状态表示
- (2)状态转移
- 三、代码
一、题目
题目描述
一棵二叉树可以按照如下规则表示成一个由 0 0 0、 1 1 1、 2 2 2 组成的字符序列,我们称之为“二叉树序列 S S S”:
S = { 0 表示该树没有子节点 1 S 1 表示该树有一个节点, S 1 为其子树的二叉树序列 2 S 1 S 2 表示该树由两个子节点, S 1 和 S 2 分别表示其两个子树的二叉树序列 S= \begin{cases} 0& \text表示该树没有子节点\\ 1S_1& 表示该树有一个节点,S_1 为其子树的二叉树序列\\ 2S_1S_2& 表示该树由两个子节点,S_1 和 S_2 分别表示其两个子树的二叉树序列 \end{cases} S=⎩ ⎨ ⎧01S12S1S2表示该树没有子节点表示该树有一个节点,S1为其子树的二叉树序列表示该树由两个子节点,S1和S2分别表示其两个子树的二叉树序列
例如,下图所表示的二叉树可以用二叉树序列 S = 21200110 S=\texttt{21200110} S=21200110 来表示。
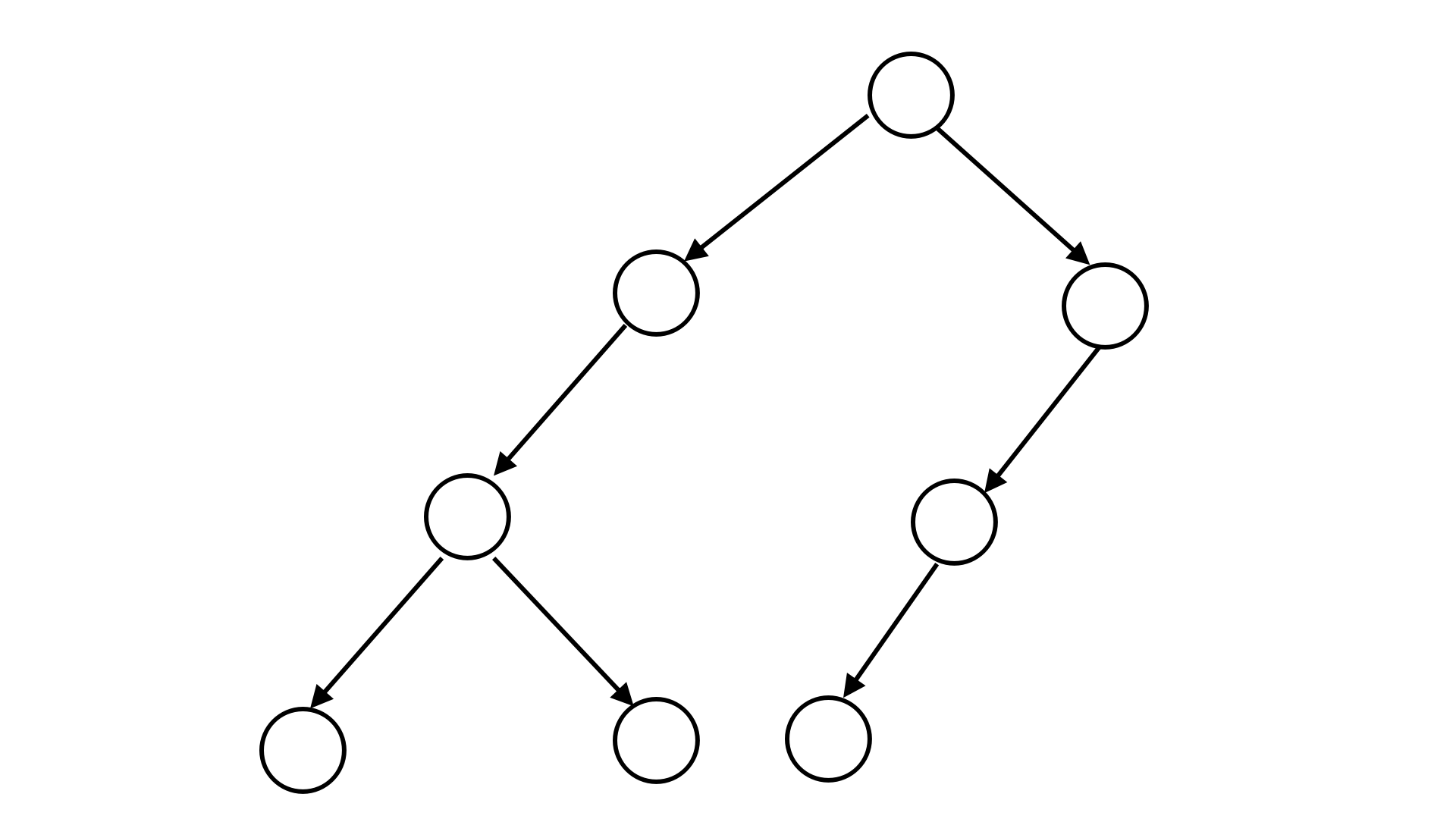
你的任务是要对一棵二叉树的节点进行染色。每个节点可以被染成红色、绿色或蓝色。并且,一个节点与其子节点的颜色必须不同,如果该节点有两个子节点,那么这两个子节点的颜色也必须不同。给定一颗二叉树的二叉树序列,请求出这棵树中最多和最少有多少个点能够被染成绿色。
输入格式
输入只有一行一个字符串 s s s,表示二叉树序列。
输出格式
输出只有一行,包含两个数,依次表示最多和最少有多少个点能够被染成绿色。
样例 #1
样例输入 #1
1122002010
样例输出 #1
5 2
提示
数据规模与约定
对于全部的测试点,保证
1
≤
∣
s
∣
≤
5
×
1
0
5
1 \leq |s| \leq 5 \times 10^5
1≤∣s∣≤5×105,
s
s
s 中只含字符 0 1 2。
二、分析
这道题有两个难点:
第一个难点是如何递归建树。
第二个难点则是我们如何写DP转移方程。
1、递归建树
题目中给了我们一个字符串,这个字符串的长度就是树中所有节点的个数。那么我们就先从左到右给这些点进行一个编号。
这个编号的过程我们用一个全局变量 t o t tot tot表示。
因为这是一个二叉树,所以它总共就分为三种情况,没有子树,一个子树,两个子树。
我们定义一个DFS函数:这个DFS的作用是建立以 u u u为根节点的树。
如果当前字符串中对应的字符是 0 0 0,则说明当前的点是叶子节点,我们将叶子节点插入到树中后,就无需向下递归(因为叶子节点没有子树),直接返回即可。
如果当前字符串中对应的字符是 1 1 1,则说明当前节点有一个子树,所以我们就需要去继续DFS。
如果当前字符串中对应的字符是 2 2 2,说明当前节点有两个子树,则我们需要先去递归第一个子树,当第一个子树建成以后,再去建第二个子树。
//递归建树
void dfs(int root)
{
tot ++;
if(str[root] == '0')return;
if(str[root] == '1')
{
edge[root + 1].push_back(root + 2);
dfs(root + 1);
}
if(str[root] == '2')
{
edge[root + 1].push_back(root + 2);
dfs(root + 1);
edge[root + 1].push_back(tot + 1);
dfs(tot);
}
}
2、树形DP + 状态机DP
我们以最大值为例,最小值就是将取最大值的过程改成取最小值。
因为子树的颜色状态影响到了当前点的染色选择,所以我们需要对所有的染色情况进行讨论,同时用0,1,2三个数字表示当前的染色情况。
(1)状态表示
f
[
u
]
[
0
]
f[u][0]
f[u][0] : 以u为根节点,u为绿色, 最多的绿色点个数。
f
[
u
]
[
1
]
f[u][1]
f[u][1]: 以u为根节点, u为红色, 最多的绿色点个数。
f
[
u
]
[
2
]
f[u][2]
f[u][2]: 以u为根节点, u为蓝色, 最多的绿色点个数。
(2)状态转移
如果当前节点是叶子节点,那么只需要给当前节点染色,状态方程为:
f
[
u
]
[
0
]
=
1
f
[
u
]
[
1
]
=
0
f
[
u
]
[
2
]
=
0
f[u][0]=1\\ f[u][1]=0\\ f[u][2]=0
f[u][0]=1f[u][1]=0f[u][2]=0
如果当前节点只有一个子树,那么状态转移方程为:
f
[
u
]
[
0
]
=
m
a
x
(
f
[
s
o
n
]
[
1
]
,
f
[
s
o
n
]
[
2
]
)
+
1
f
[
u
]
[
1
]
=
m
a
x
(
f
[
s
o
n
]
[
0
]
,
f
[
s
o
n
]
[
2
]
)
f
[
u
]
[
2
]
=
m
a
x
(
f
[
s
o
n
]
[
1
]
,
f
[
s
o
n
]
[
0
]
)
f[u][0]=max(f[son][1],f[son][2])+1 \\f[u][1]=max(f[son][0],f[son][2]) \\f[u][2]=max(f[son][1],f[son][0])
f[u][0]=max(f[son][1],f[son][2])+1f[u][1]=max(f[son][0],f[son][2])f[u][2]=max(f[son][1],f[son][0])
如果当前节点有两个子树的话,那么状态转移方程为:
f
[
u
]
[
0
]
=
m
a
x
(
f
[
s
o
n
1
]
[
1
]
+
f
[
s
o
n
]
[
2
]
,
f
[
s
o
n
1
]
[
2
]
+
f
[
s
o
n
2
]
[
1
]
)
+
1
f
[
u
]
[
1
]
=
m
a
x
(
f
[
s
o
n
1
]
[
0
]
+
f
[
s
o
n
2
]
[
2
]
,
f
[
s
o
n
1
]
[
2
]
+
f
[
s
o
n
2
]
[
0
]
)
f
[
u
]
[
2
]
=
m
a
x
(
f
[
s
o
n
1
]
[
0
]
+
f
[
s
o
n
2
]
[
1
]
,
f
[
s
o
n
1
]
[
1
]
+
f
[
s
o
n
2
]
[
0
]
)
f[u][0]=max(f[son1][1]+f[son][2],f[son1][2]+f[son2][1])+1 \\f[u][1]=max(f[son1][0]+f[son2][2],f[son1][2]+f[son2][0]) \\f[u][2]=max(f[son1][0]+f[son2][1],f[son1][1]+f[son2][0])
f[u][0]=max(f[son1][1]+f[son][2],f[son1][2]+f[son2][1])+1f[u][1]=max(f[son1][0]+f[son2][2],f[son1][2]+f[son2][0])f[u][2]=max(f[son1][0]+f[son2][1],f[son1][1]+f[son2][0])
三、代码
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 5e5 + 10;
string str;
int f[N][3];
int g[N][3];
int tot = 0;
vector<int>edge[N];
//递归建树
void dfs(int root)
{
tot ++;
if(str[root] == '0')return;
if(str[root] == '1')
{
edge[root + 1].push_back(root + 2);
dfs(root + 1);
}
if(str[root] == '2')
{
edge[root + 1].push_back(root + 2);
dfs(root + 1);
edge[root + 1].push_back(tot + 1);
dfs(tot);
}
}
void dp(int u)
{
if(edge[u].size() == 1)
{
int son = edge[u][0];
dp(son);
f[u][0] = max(f[son][1], f[son][2]) + 1;
f[u][1] = max(f[son][2], f[son][0]);
f[u][2] = max(f[son][0], f[son][1]);
g[u][0] = min(g[son][1], g[son][2]) + 1;
g[u][1] = min(g[son][2], g[son][0]);
g[u][2] = min(g[son][0], g[son][1]);
}
else if(edge[u].size() == 2)
{
int son1 = edge[u][0], son2 = edge[u][1];
dp(son1);
dp(son2);
f[u][0] = max(f[son1][1] + f[son2][2], f[son1][2] + f[son2][1]) + 1;
f[u][1] = max(f[son1][0] + f[son2][2], f[son1][2] + f[son2][0]);
f[u][2] = max(f[son1][0] + f[son2][1], f[son1][1] + f[son2][0]);
g[u][0] = min(g[son1][1] + g[son2][2], g[son1][2] + g[son2][1]) + 1;
g[u][1] = min(g[son1][0] + g[son2][2], g[son1][2] + g[son2][0]);
g[u][2] = min(g[son1][0] + g[son2][1], g[son1][1] + g[son2][0]);
}
else
{
f[u][0] = 1;
g[u][1] = g[u][2] = 0;
g[u][0] = 1;
return;
}
}
/*
f[u][0] : 以u为根节点, u为绿色, 最多的绿色点
f[u][1] : 以u为根节点, u为红色, 最多的绿色点
f[u][2] : 以u为根节点, u为蓝色, 最多的绿色点
f[u][0] = max(f[u][0], f[son1][1] + f[son2][2]);
f[u][1] = max(f[u][1], f[son1][0] + f[son2][2]);
f[u][2] = max(f[u][2], f[son1][0] + f[son2][1]);
*/
void solve()
{
memset(g, INF, sizeof g);
cin >> str;
dfs(0);
dp(1);
// for(int i = 1; i <= str.size(); i ++)
// {
// cout << i << ": ";
// for(int j = 0; j < edge[i].size(); j ++ )
// {
// cout << edge[i][j] << " ";
// }
// cout << endl;
// }
cout << max(max(f[1][0], f[1][1]), f[1][2]) << " ";
cout << min(min(g[1][0], g[1][1]), g[1][2]) << endl;
return;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
solve();
}