二分——力扣篇
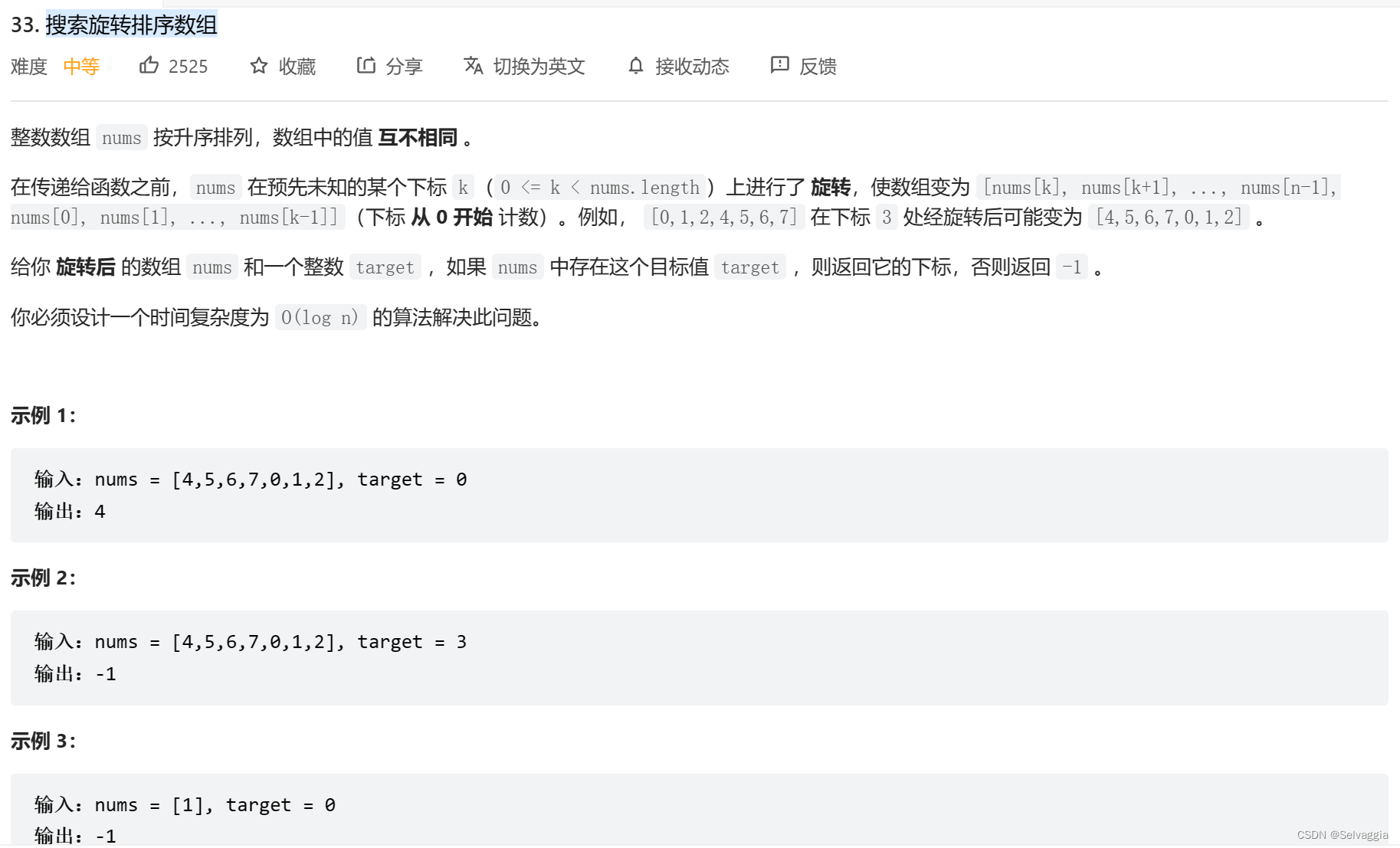
- 搜索旋转排序数组
- 搜索旋转排序数组II
- 寻找旋转排序数组中的最小值
- 寻找旋转排序数组中的最小值II
搜索旋转排序数组

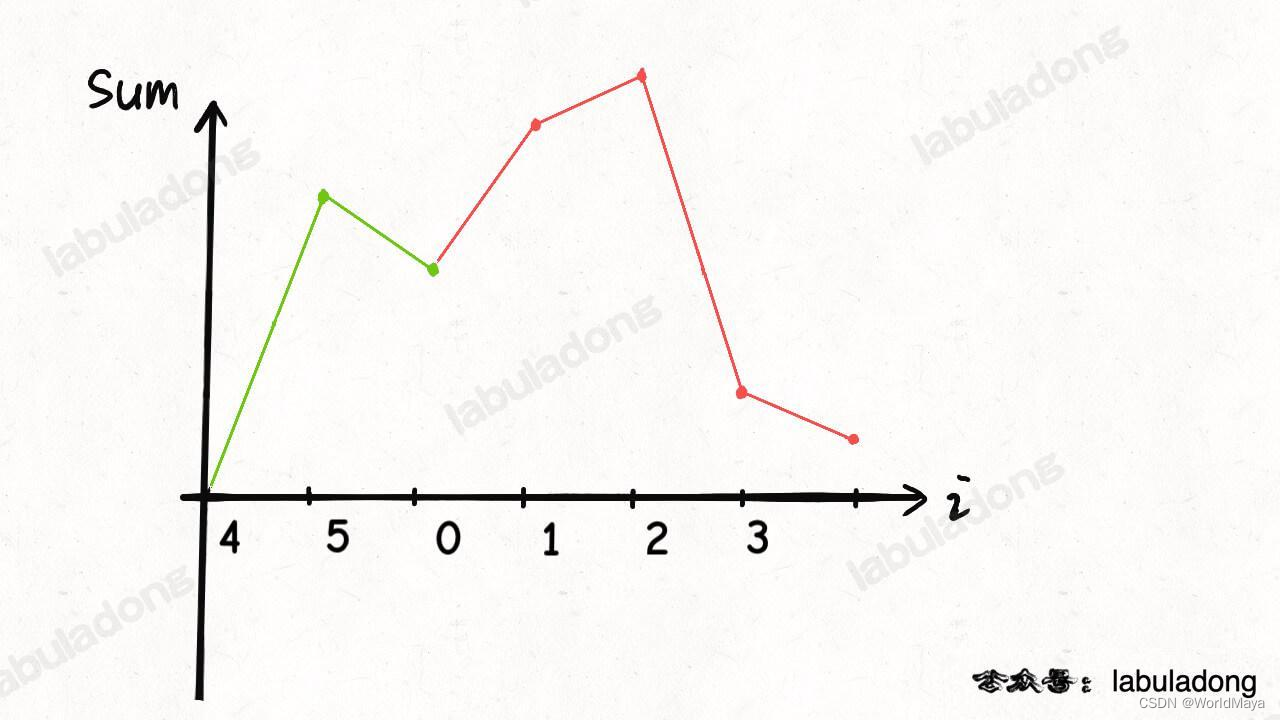
定理一:只有在顺序区间内才可以通过区间两端的数值判断target是否在其中。
定理二:判断顺序区间还是乱序区间,只需要对比 left 和 right 是否是顺序对即可,left <= right,顺序区间,否则乱序区间。
通过不断的用Mid二分,根据定理二,将整个数组划分成顺序区间和乱序区间,然后利用定理一判断target是否在顺序区间,如果在顺序区间,下次循环就直接取顺序区间,如果不在,那么下次循环就取乱序区间。
- 注意点一:整体二分前,必须对区间长度进行特判,比如二分之前,如果整个序列长度为1,按我这种二分方式
l<r根本不可能进入二分。 - 注意点二:判断是否为顺序区间,只需比较该区间左右端点的大小,
错误想法是以为不会有重复的元素,所以只需要判断是否左下标对应的元素严格小于右下标对应的元素,其实不然,涉及区间必须对区间长度进行特判,比如二分之前,如果整个序列长度为1,按我这种二分方式l<r根本不可能进入二分。回到判断是否为顺序区间,如果区间长度为1或者2,l的值和mid的值是相等的,指向的自然是同一元素,会是相等的。例子为3 1 找 1。我又想,是不是在整个二分之前特判区间长度为2的情况就OK呢?不对,因为二分就是缩小区间范围的过程,并不一定开局就是target在仅有的两个元素之间,很有可能一直二分直到缩小到区间长度为2
3、按照这套二分模板,
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
不断缩小区间范围只能遵循一种规律那就是由int mid = l + r >> 1;决定的从小到大找和l = mid + 1; (一定是匹配出现的),或者是由int mid = l + r+1 >> 1;决定的从大到小找和l = mid ; 这里
if(target>=nums[mid]&&target<=nums[r]){
if(nums[mid] == target) return mid;
else l=mid+1;
}
如果此时不提前判断mid及时返回mid,那么l应当取的值是l=mid,显然不对(记住死循环解释) OK,提前判断mid,ac啦
class Solution {
public:
int search(vector<int>& nums, int target) {
int n=nums.size();
if(n==0)return -1;
if(n==1)return nums[0]==target?0:-1;
int l=0,r=n-1;
while(l<r){
int mid=(l+r)>>1;
// if(nums[mid] == target) return mid;
// 数组旋转过后一定是一段或者两段上升的子段,仍然可以二分
// 但是整体二分[l,mid]不一定恰好处于上升子段之中,可能包含了俩子段各一部分
if(nums[l]<=nums[mid]){//不取等号是因为不存在重复元素 [l,mid]恰好处于升序子段
if(target>=nums[l]&&target<=nums[mid]){
r=mid;
}
else l=mid+1;
}
else{//[l,mid]不完全处于升序子段,好办,[mid+1,r]一定属于
if(target>=nums[mid]&&target<=nums[r]){
if(nums[mid] == target) return mid;
else l=mid+1;
}
else r=mid-1;
}
}
return (nums[l] == target)?l:-1;
}
};
//3 1
//1
//-1 其实是1
另一种二分代码
class Solution {
public:
int search(vector<int>& nums, int target) {
int n=nums.size();
if(n==0)return -1;
if(n==1)return nums[0]==target?0:-1;
// if(n==2){
// if(target==nums[0])return 0;
// else if(target==nums[1])return 1;
// else return -1;
// }
int l=0,r=n-1;
while(l<=r){
int mid=(l+r)>>1;
if(nums[mid] == target) return mid;
// 数组旋转过后一定是一段或者两段上升的子段,仍然可以二分
// 但是整体二分[l,mid]不一定恰好处于上升子段之中,可能包含了俩子段各一部分
if(nums[l]<nums[mid]){//[l,mid]恰好处于升序子段
//不取等号是因为不存在重复元素 ,错,要取, 比如 3 1 找1,l就是mid
// 5 1 2 3 4找1,只要target找的范围缩小到了旋转点+左 或 右转点+左
if(target>=nums[l]&&target<nums[mid]){
r=mid-1;
}
else l=mid+1;
}
else{//[l,mid]不完全处于升序子段,好办,[mid+1,r]一定属于
if(target>nums[mid]&&target<=nums[r]){
l=mid+1;
}
else r=mid-1;
}
}
return -1;
}
};
搜索旋转排序数组II


10111 和 11101 这种。此种情况下 nums[start] == nums[mid],分不清到底是前面有序还是后面有序,此时 start++ 即可。相当于去掉一个重复的干扰项。
顺带发现,if(nums[mid] == target) return true;用我的二分模板,每次得到mid先判断也无伤大雅,提前发现提前返回而已,主要是注意缩小区间的方式
class Solution {
public:
int search(vector<int>& nums, int target) {
int n=nums.size();
if(n==0)return -1;
if(n==1)return nums[0]==target?true:false;
int l=0,r=n-1;
while(l<r){
int mid=(l+r)>>1;
if(nums[mid] == target) return true;
if (nums[l] == nums[mid] && nums[mid] == nums[r]) {
++l;
--r;
}
else if(nums[l]<=nums[mid]){//不取等号是因为不存在重复元素 [l,mid]恰好处于升序子段
if(target>=nums[l]&&target<=nums[mid]){
r=mid;
}
else l=mid+1;
}
else{//[l,mid]不完全处于升序子段,好办,[mid+1,r]一定属于
if(target>=nums[mid]&&target<=nums[r]){
if(nums[mid] == target) return true;
else l=mid+1;
}
else r=mid-1;
}
}
return (nums[l] == target)?true:false;
}
};
//3 1
//1
//-1 其实是1
寻找旋转排序数组中的最小值
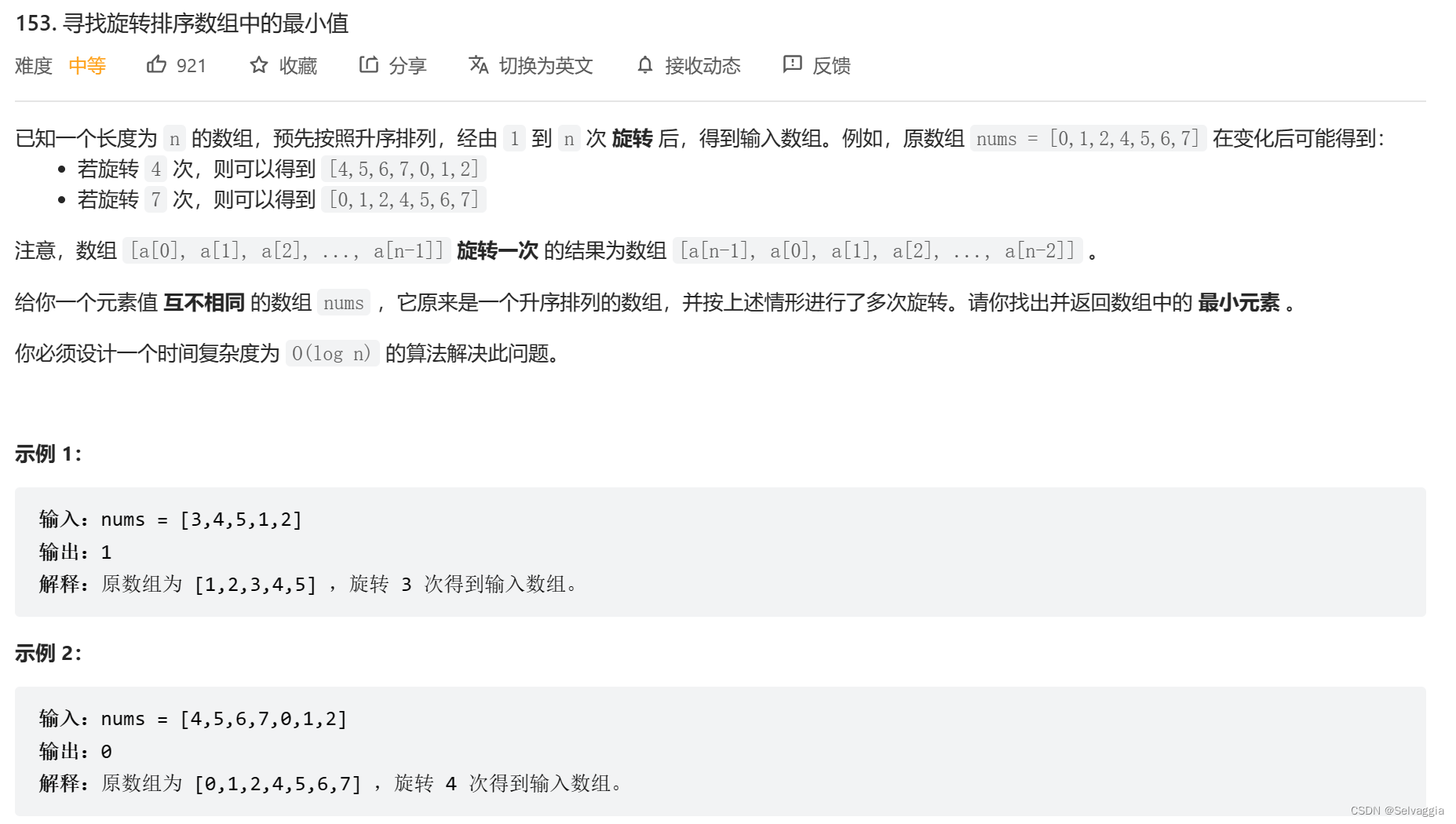

三种情况主要就是mid落在的位置不同,需要使区间来到第二段
class Solution {
public:
int findMin(vector<int>& nums) {
int n=nums.size();
int l=0,r=n-1;
while(l<r){
int mid=l+r>>1;
//经由 1 到 n 次 旋转,两段升序子序列,且第一段大于第二段,最小值一定在第二段
if(nums[mid]<nums[r]){
// l=mid;
r=mid;
}
else{
// r=mid-1;//不对的,记住永远在 第二段 找,lr需要使区间缩小到第二段
l=mid+1;
}
}
return nums[l];
}
};
寻找旋转排序数组中的最小值II

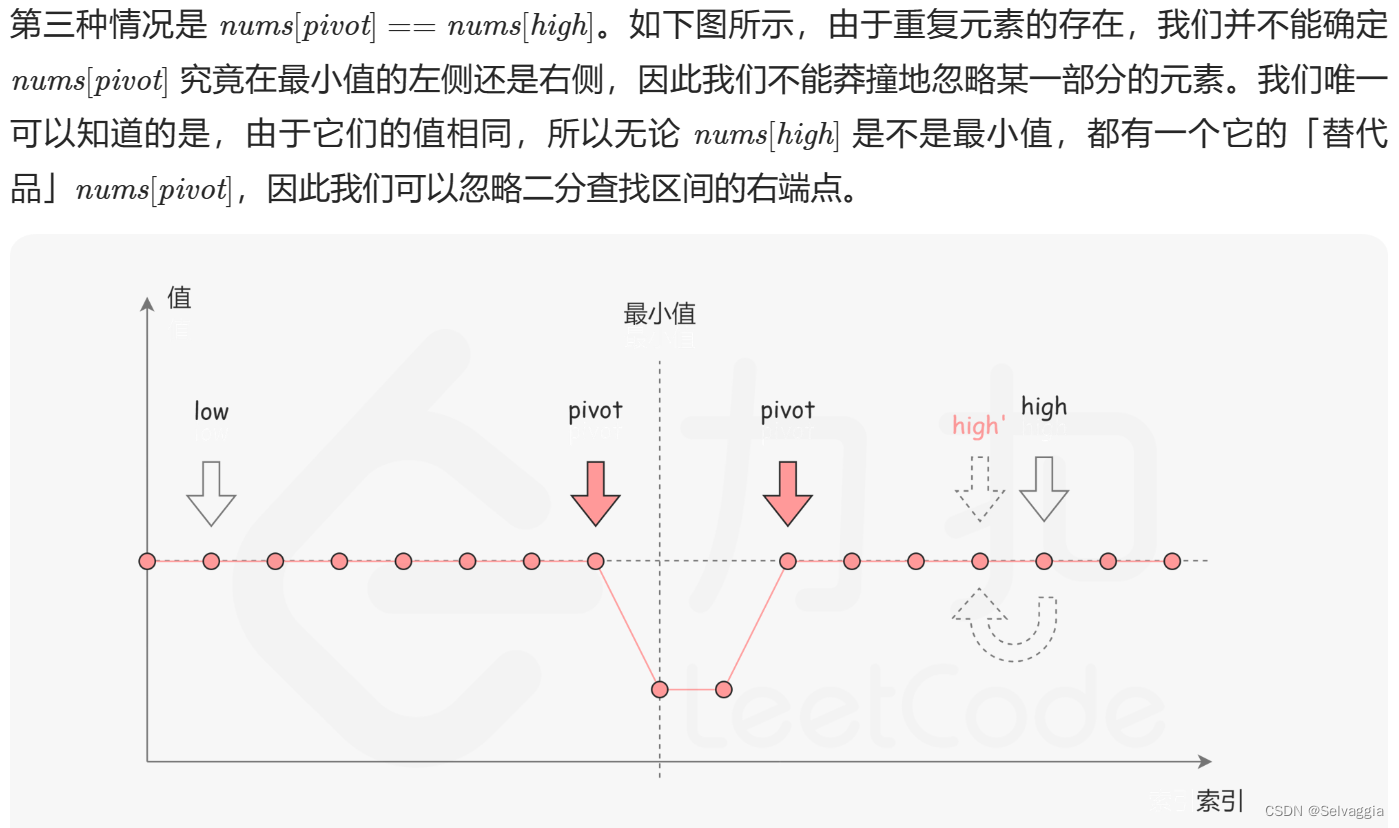
class Solution {
public:
int findMin(vector<int>& nums) {
int n=nums.size();
int l=0,r=n-1;
while(l<r){
int mid=l+r>>1;
//经由 1 到 n 次 旋转,两段升序子序列,且第一段大于第二段,最小值一定在第二段
if(nums[mid]<nums[r]){
// l=mid;
r=mid;
}
else if(nums[mid]>nums[r]){
// r=mid-1;//不对的,记住永远在 第二段 找,lr需要使区间缩小到第二段
l=mid+1;
}
else {//if(nums[mid]==nums[r])
r--;
}
}
return nums[l];
}
};