C++ 算法主题系列之集结0-1背包问题的所有求解方案

news2025/7/14 19:20:25

1. 前言

背包问题是类型问题，通过对这一类型问题的理解和掌握，从而可以归纳出求解此类问题的思路和模板。

背包问题的分类有：

  • 0-1背包问题，也称为不可分割背包问题。
  • 无限背包问题。
  • 判定性背包问题.
  • 带附属关系的背包问题。
  • 双背包求最优值.
  • 构造三角形问题.
  • 带上下界限制的背包问题(012背包)
  • ……

本文将介绍0-1背包问题的各种求解方案，通过对各种求解方案的研究，从而全方面了解0-1背包问题的本质。

2. 0-1 背包问题

问题描述：

有一背包，能容纳的重量为 m，现有 n种物品，每种物品有重量和价值 2 个属性。请设计一个算法，在不分割物品的情况下，保证背包中所容纳的物品的总价值是最大的。

0-1背包也称为完全背包或不可分割背包问题，是一类常见的背包问题。常用的实现方案有递归和动态规划 。

2.1 递归算法

可以有 3 种写法。

2.1.1 第一种递归回溯方案

回顾递归回溯算法适合的问题域：

  • 待解决的问题可以分多步。如迷宫问题、排列组合问题……
  • 每一步都可能存在多个选择，当某一个选择行不通，或此选择结束后，可以回溯到上一步再另行选择。

那么背包问题是否适合上述的要求？

  • 可以想象背包里有很多个格间。当每一个格间填充完毕，则表示得到一种求解。
  • 对于格间而言，每一种物品都是一种选择，可以通地回溯再选择另一个物品。
  • 其本质是对物品进行任意组合，然后再选择总价值最大的一种组合。

如下图，有 3 个物品需要放置入容量为 50 的背包中。初始可把背包想象成一个大格间，此时可以试着放入物品中的一个。

1.png

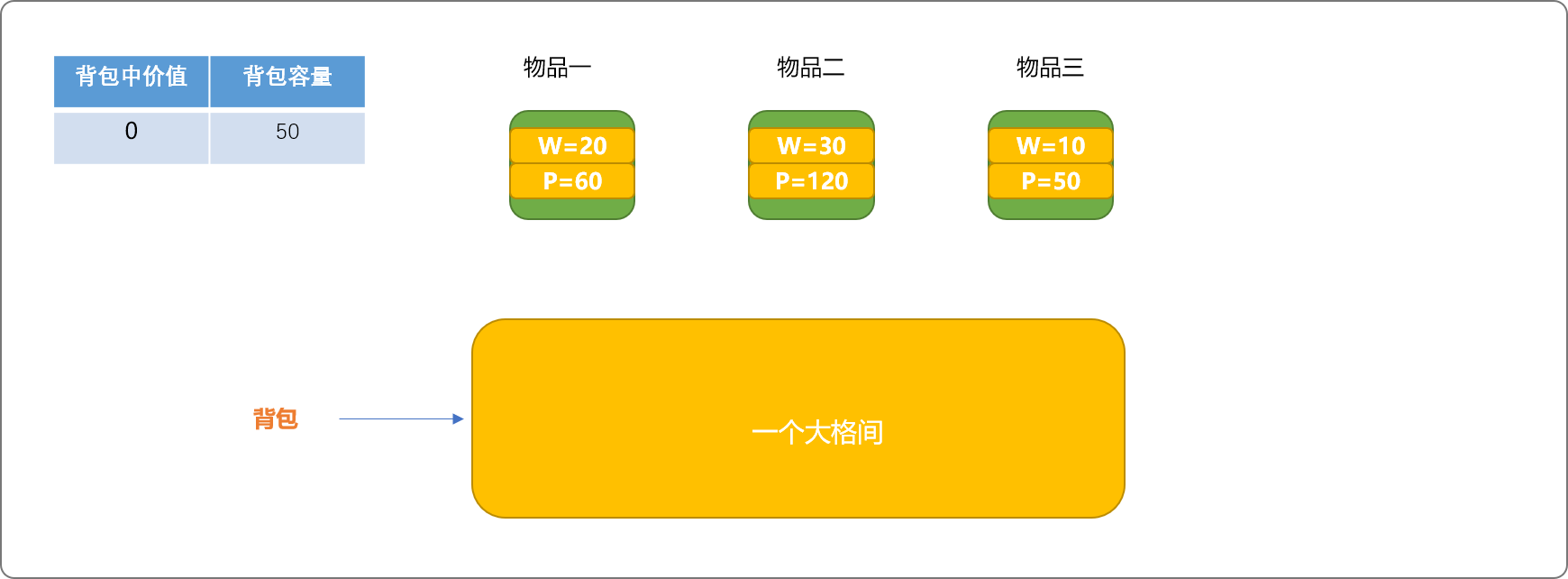
物品放入格间的条件：

  • 物品不曾在背包中。
  • 物品的重量小于或等于背包现有容量。

如下图，把物品一放入背包中。且把背包剩下空间想象为一个格间，在余下的物品中选择一个放入此格间中。

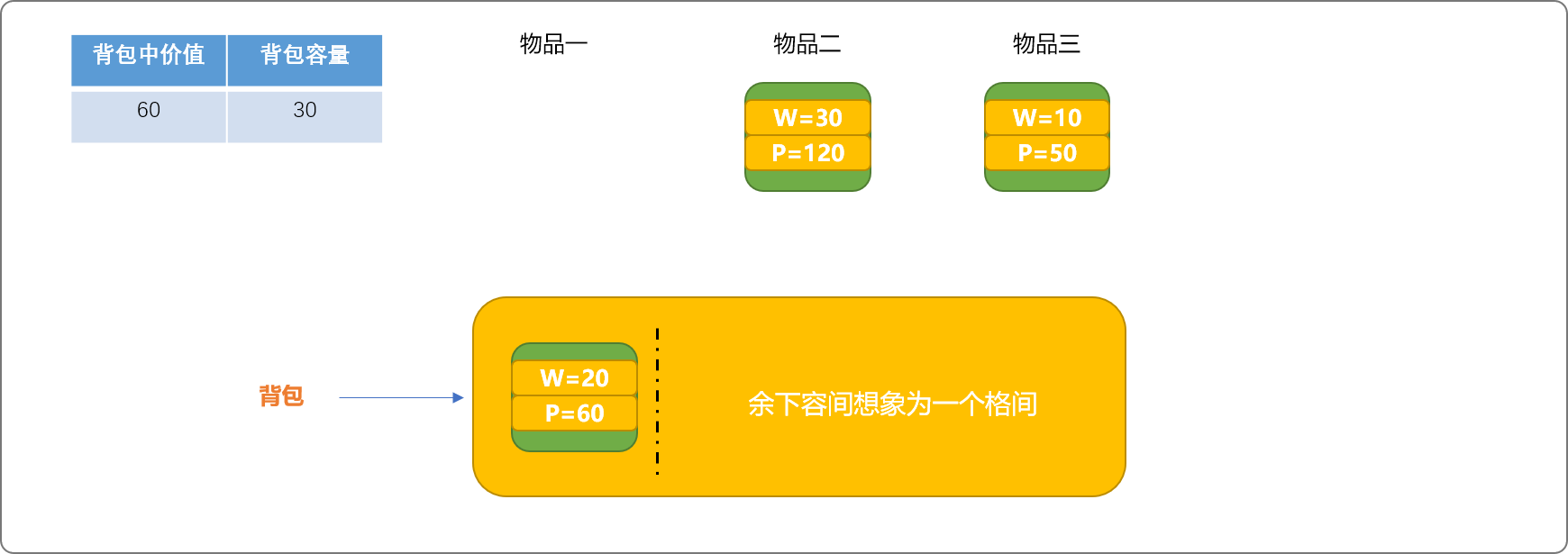
1_0.png

如下，把物品二放入格间中。

2.png

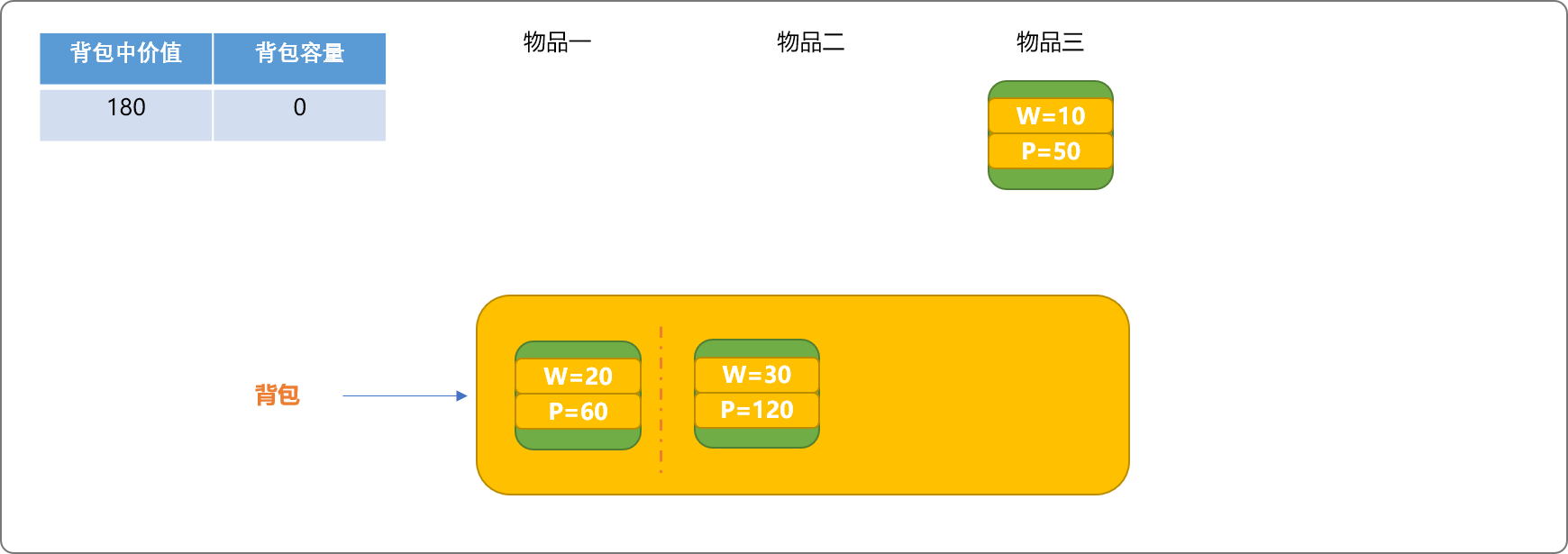
因物品一和物品二的重量之和为 50。等于背包总容量。此时，背包中已经没有剩余空间。也意味着不能再向此背包中放入物品。

至此，可以输出背包中的物品，且把背包中的总价值 180 存储在全局变量中，以便在后续操作时，查找是否还有比此值更大的值。

回溯物品

所谓回溯物品，指把物品从背包中移走，试着再放入一个其它物品。

如下图，回溯物品二，腾出格间。因物品三满足放入条件，放入格间。

3.png

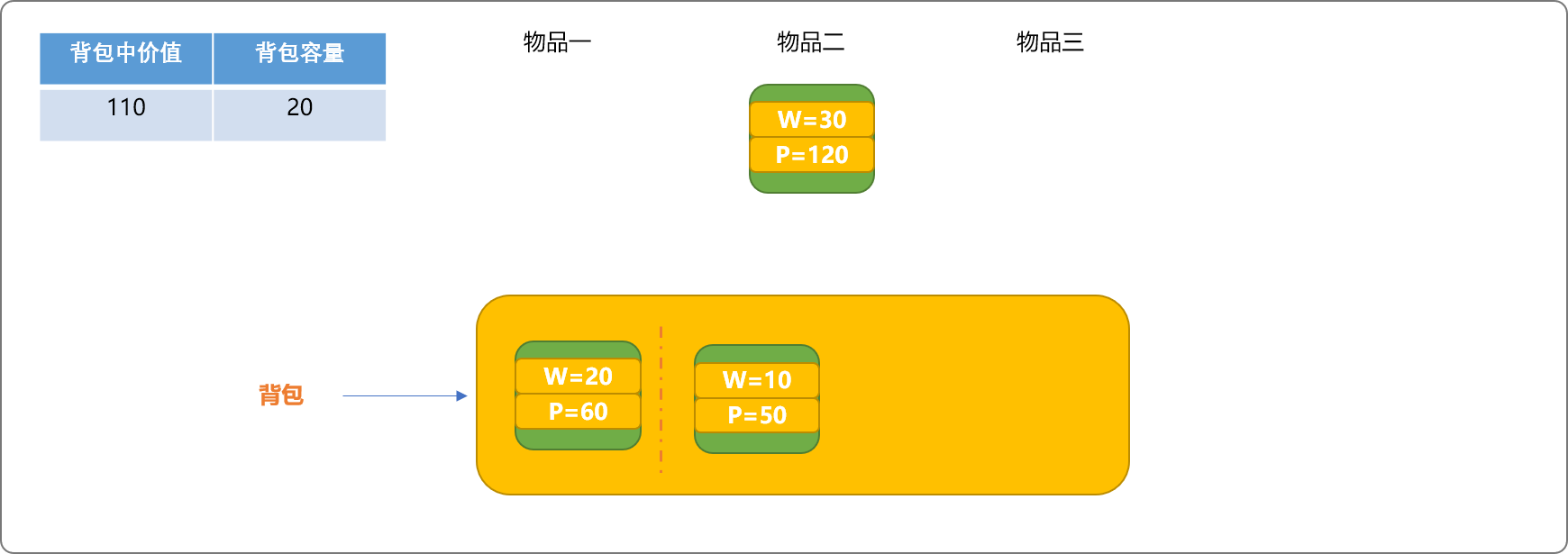
此时，背包还有剩余空间，同样把剩余空间想象成一个格间。因有剩余空间，可以试着把物品二放入背包中。

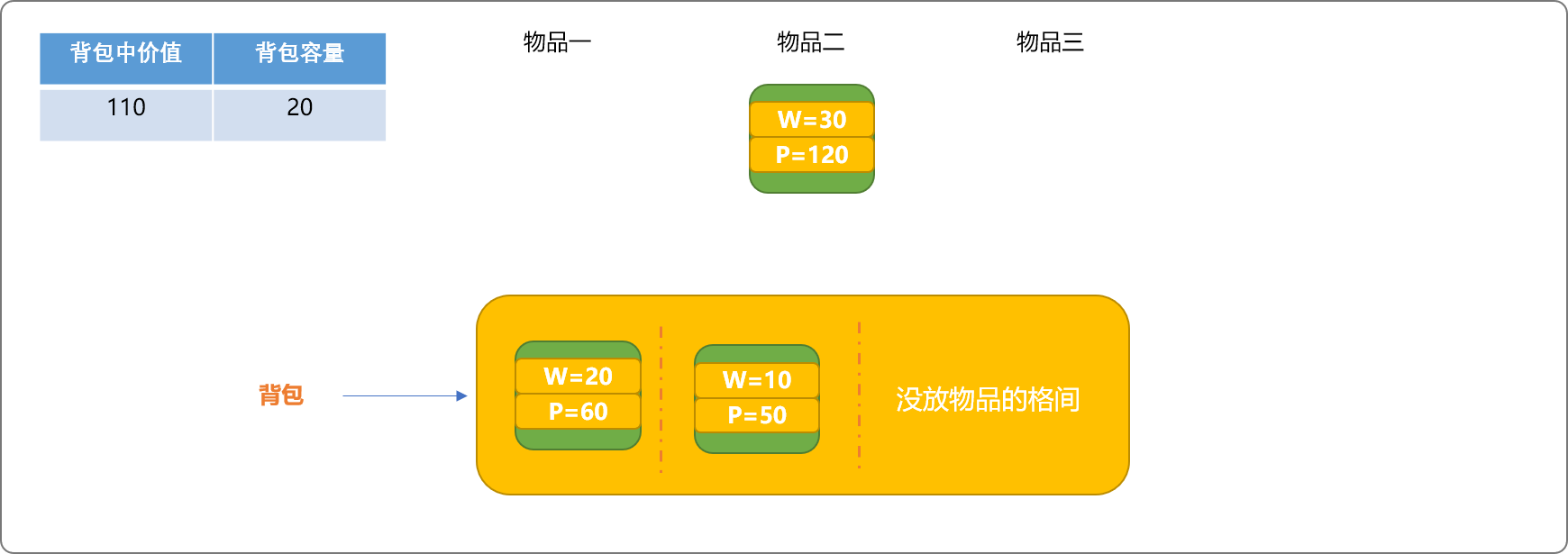
4_0.png

但因物品二的重量大于背包已有的容量，不能放入。此时，可以输出背包中的物品信息，并记录背包中的最大价值为110。因比前面的180的值小，继续保留 180这个价值为当前最大值。

对上述流程做一个简单总结：

  • 当背包还有空间，且有物品可以放入时，则加入到背包中。

  • 当背包不再能放下任何一件物品时，计算此时的总价值，并确定是不是最大价值。

    Tips：这里有一点需要注意，递归函数的出口有 2 个，一是还有物品可选择，但不能放入背包中。二是不再有物品可供选择。

  • 回溯当前已经放入物品，选择其它物品，重复上述过程，一直到找到真正的最大值。

代码如下所示：

#include<bits/stdc++.h>
using namespace std;
struct Goods {
	//重量
	int weight;
	//价值
	int price;
	//装入状态
	bool isUse;
};
/*
*初始化
*/
Goods allGoods[3]= { {20,60,false},{30,120,false},{10,50,false}};

//背包重量
int weight=50;
//最大价值
int maxPrice=0;
//总价值
int totalPrice=0;
/*
* 0-1 背包
* idx:物品编号，只需要考虑组合
* deep:递归深度
*/
void bag(int idx,int deep,int weight) {
	//每次都可以从所有物品中进行选择
	for(int i=idx; i<3; i++) {
		if( allGoods[i].isUse==false  ) {
			//物品不曾放入背包
			if( allGoods[i].weight<=weight) {
				//且可以放下，增加背包中的总价值
				totalPrice+=allGoods[i].price;
				//标志此物品已经放入
				allGoods[i].isUse=true;
				//继续放置物品
				bag(i,deep+1,weight - allGoods[i].weight);
				//回溯
				totalPrice-=allGoods[i].price;
				allGoods[i].isUse=false;
			} else {
				//出口一：不可以放下，计算此时背包中的物品的价值是否是最大值，
				cout<<"-----------查询到某个物品不能放下时，显示背包中信息------------"<<endl;
				if(totalPrice>maxPrice) maxPrice= totalPrice;
				for(int j=0; j<3; j++)
					if(allGoods[j].isUse)
						cout<<allGoods[j].weight<<","<<allGoods[j].price<<endl;
				return ;
			}
		}
	}
    //出口二：不再有物品可以选择
	cout<<"--------当没有物品可选择时也要显示背包中物品信息-----------"<<endl;
	if(totalPrice>maxPrice) maxPrice= totalPrice;
	cout<<"此时背包中物品"<<endl;
	for(int j=0; j<3; j++)
		if(allGoods[j].isUse)
			cout<<allGoods[j].weight<<","<<allGoods[j].price<<endl;
}
//测试
int main() {
	bag(0,1,weight);
	cout<<"---------------------"<<endl;
	cout<<"最终背包中最大价值"<<maxPrice<<endl;
	return 0;
}

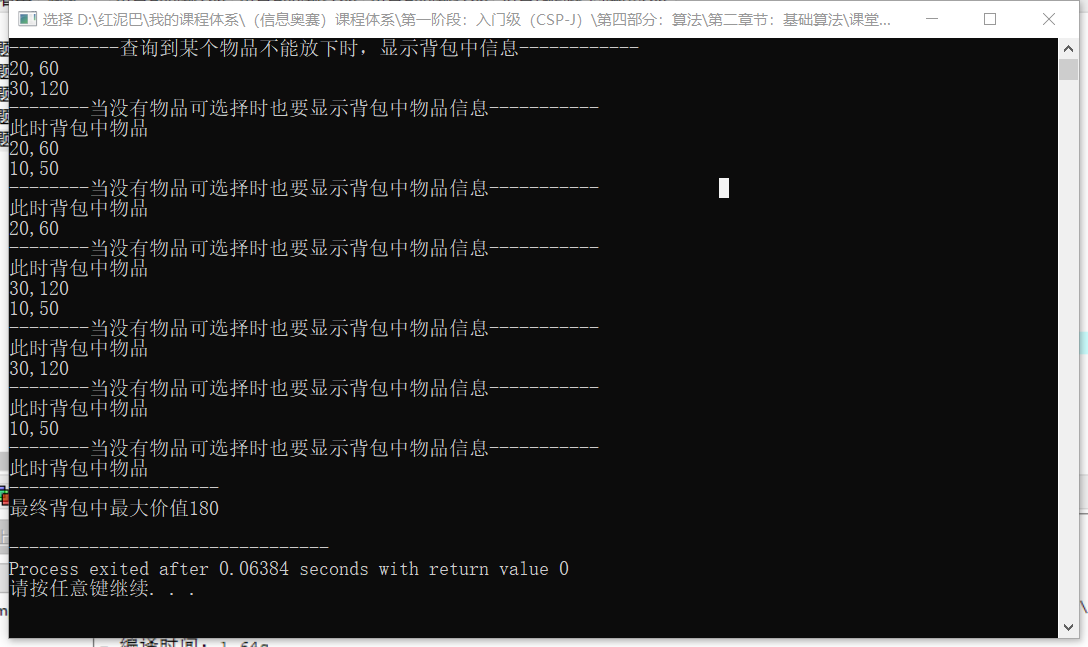
测试结果：

9.png

2.1.2 第二种回溯方案

第一种回溯方案，略显复杂，可以采用下面的回溯方案。

此方案中把物品可放入和不可放入做为选择。但其本质和上述实现是一样的。

#include<bits/stdc++.h>
using namespace std;
struct Goods {
	//物品重量
	int weight;
	//物品价值
	int value;
	//物品状态 1 已经使用，0 未使用
	int isUse;
};

//最大价值
int maxPrice=0;
//总价值
int totalPrice=0;
//背包重量
int bagWeight=100;
//物品信息
Goods allGoods[5]= { {20,60,false},{30,120,false},{10,50,false},{20,20,false},{40,100,false} };
int count=4;
/*
*显示背包中物品
*/
void showBag() {
	for(int i=0; i<5; i++) {
		if(allGoods[i].isUse)
			cout<<allGoods[i].weight<<","<<allGoods[i].value<<endl;
	}
}
/*
* idx: 物品编号
* count: 物品总数量
*/
void zeroAndOneBag(int idx,int weight) {
    //物品只有两种状态
	for(int i=0; i<=1; i++) {
		if( weight-allGoods[idx].weight*i>=0 ) {
			//物品状态
			allGoods[idx].isUse=i;
			//总价值
			totalPrice+=allGoods[idx].value*i;
			if(idx==4) {
				if(totalPrice>maxPrice) {
					maxPrice=totalPrice;
					cout<<"------------"<<endl;
					showBag();
					cout<<maxPrice<<endl;
				}
			} else {
				zeroAndOneBag(idx+1,weight-allGoods[idx].weight*i);
			}
			//回溯
			allGoods[idx].isUse=0;
			totalPrice-=allGoods[idx].value*i;
		}
	}
}
//测试
int main() {
	zeroAndOneBag(0,bagWeight);
	return 0;
}

2.1.3 第三种方案

前两种方案，不仅可得到最优值，且可以得到寻找过程中的各种组合方案。如果仅仅是想得到最终结果，不在乎中间的过程，则可以使用下面的递归方案。

#include<iostream>
#include<windows.h>//max函数
using namespace std;
struct Goods {
	//重量
	int weight;
	//价值
	int price;
	//装入状态
	bool isUse;
};
//所有物品
Goods allGoods[5]= { {20,60,false},{30,120,false},{10,50,false},{20,20,false},{40,100,false} };
//背包重量
int bagWeight = 100;
//物品总数量
int totalNumber = 5;
/*
*递归
*/
int zeroAndOneBag(int index, int remainWeight) {
	int totalPrice = 0;
	//没有物品可放
	if (index == totalNumber) return 0;
	if (allGoods[index].weight > remainWeight)
		//当前物品不能放入，查看其它物品放入的情况
		totalPrice = zeroAndOneBag(index + 1, remainWeight);
	else
		//当前物品可以放入，则在把此物品放入和不放入背包时的最大价值 
		totalPrice = max(zeroAndOneBag(index + 1, remainWeight -allGoods[index].weight) + allGoods[index].price, zeroAndOneBag(index + 1, remainWeight));
	return totalPrice;
}
//测试
int main() {
	int value = zeroAndOneBag(0, bagWeight);
	cout << value << endl;
	return 0;
}

2.2 动态规划

背包问题，有 2 个状态值，背包的容量和可选择的物品。

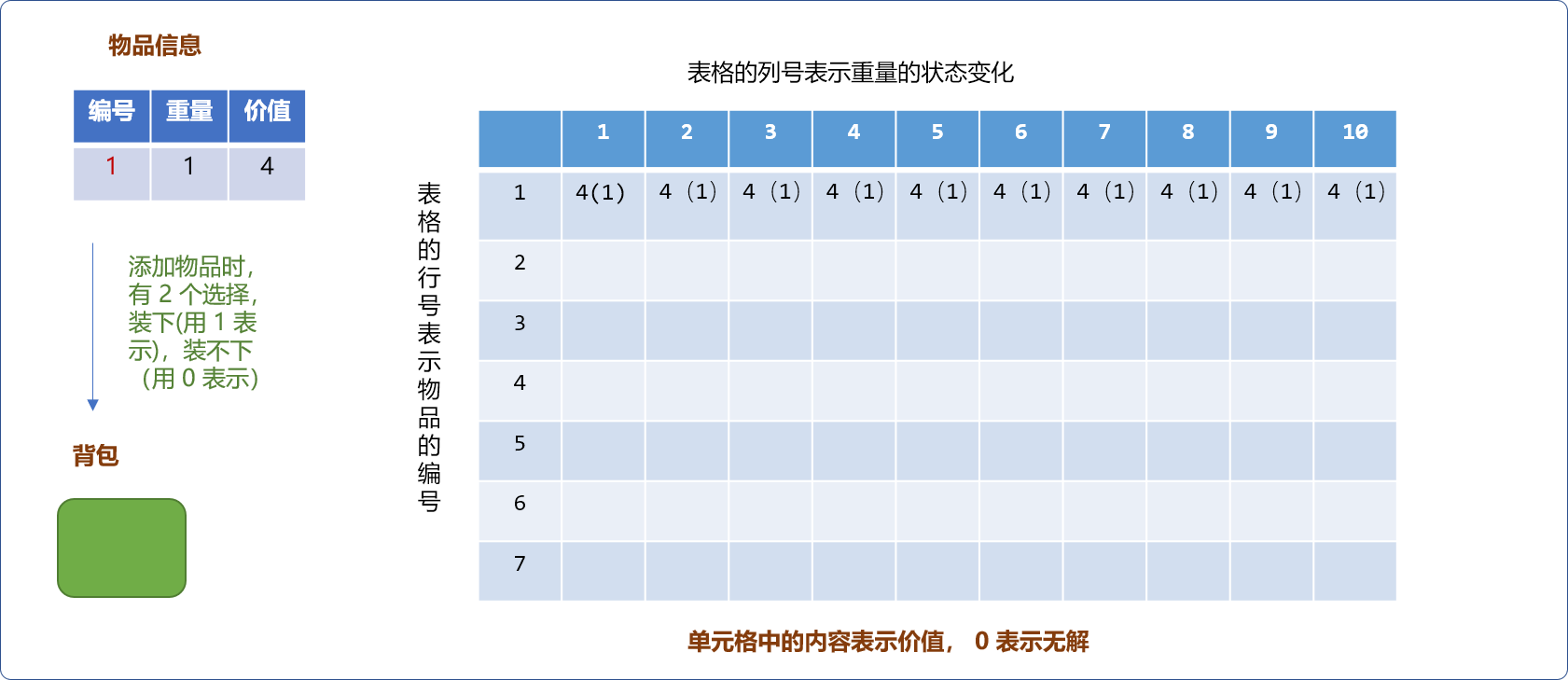
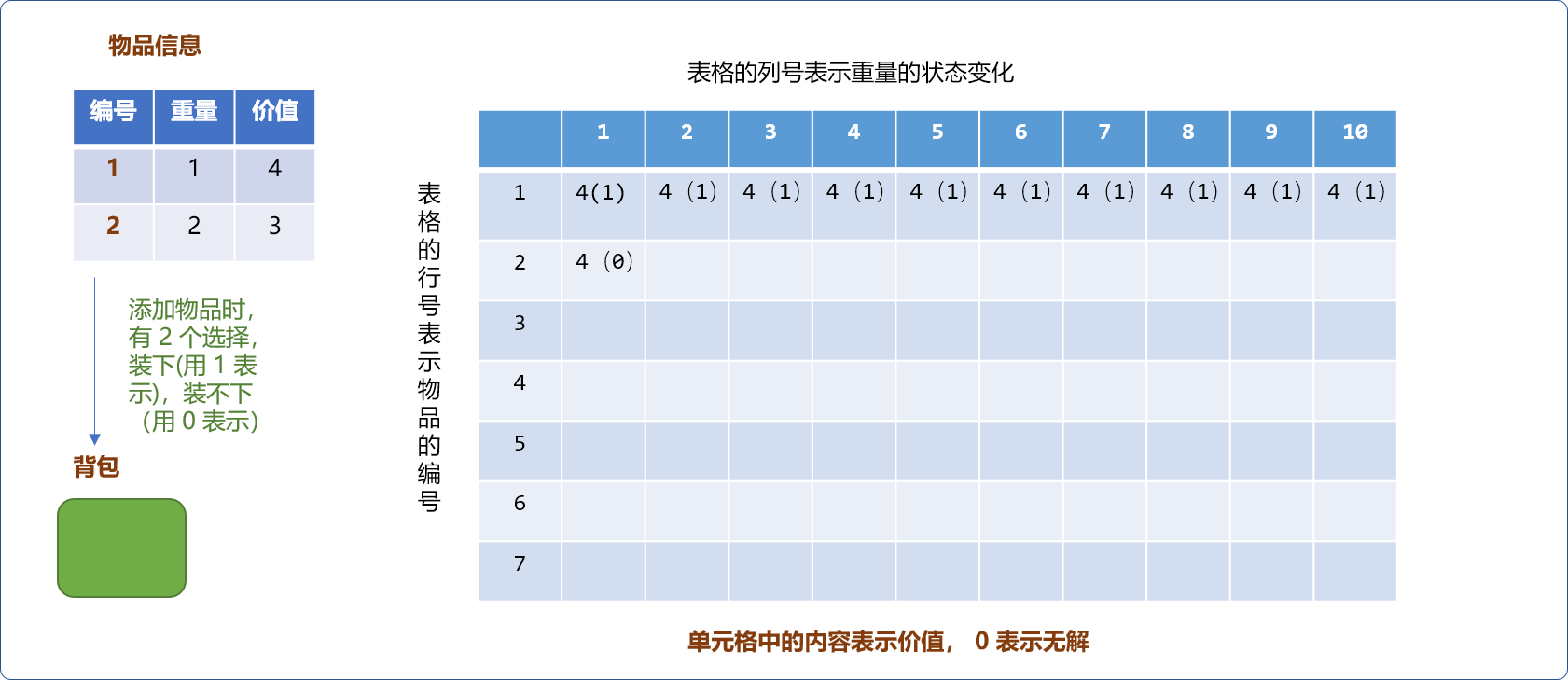
  • 物品对于背包而言，只有 2 种选择，要么装下物品，要么装不下，如下图所示，表格的行号表示物品编号，列号表示背包的重量。单元格中的数字表示背包中最大价值。当物品只有一件时，当物品重量大于背包容量，不能装下，反之，能装下。如下图，物品重量为 1。无论何种规格容量的背包都能装下（假设背包的容量至少为 1）。

dt22.png

  • 如下图，当增加重量为 2 的物品后，当背包的容量为 1 时，不能装下物品，则最大值为同容量背包中已经有的最大值。

dt23.png

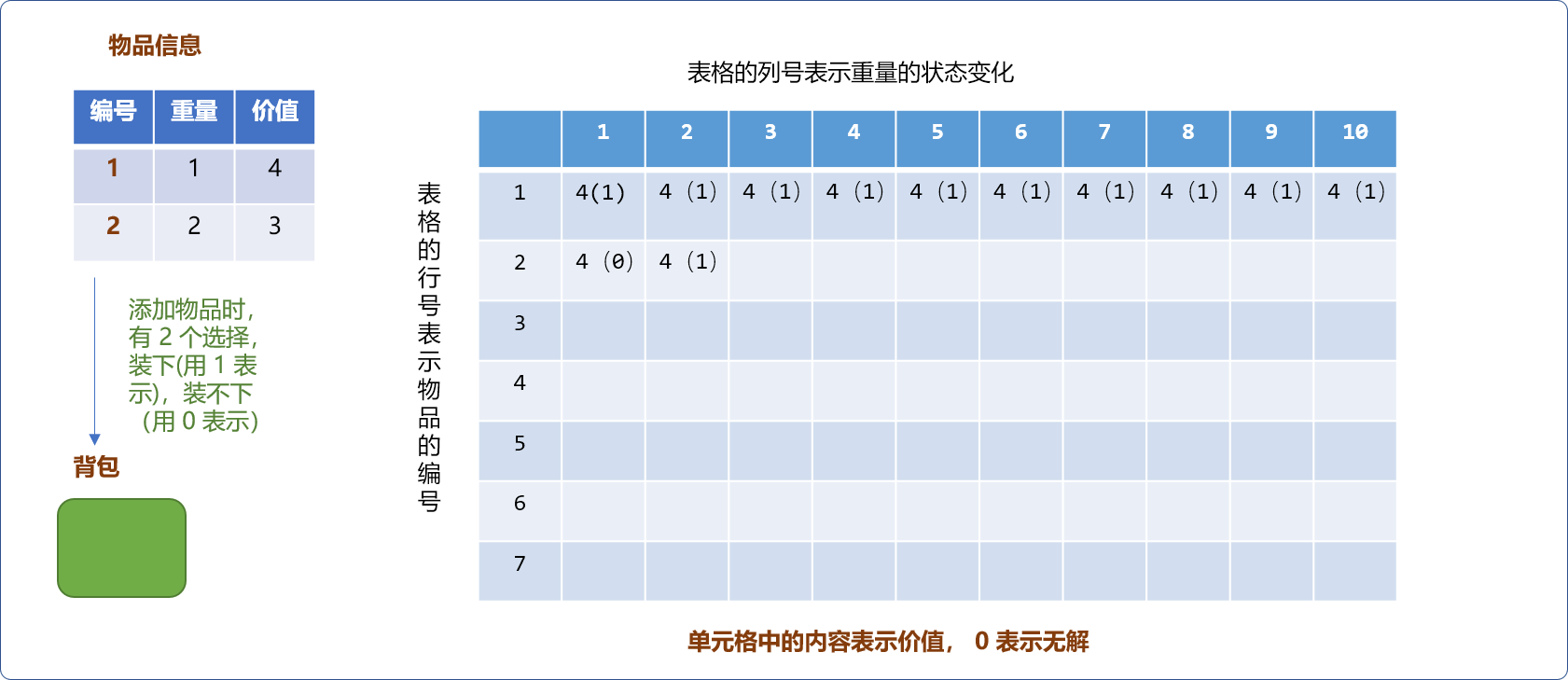
但对容量为 2的背包而言，恰好可以放入新物品，此时背包中的最大价值就会有 2 个选择，一是把物品 2 放进去，背包中的价值为 3。二是保留背包已有的价值4。然后，在两者中选择最大值 4。

dt24.png

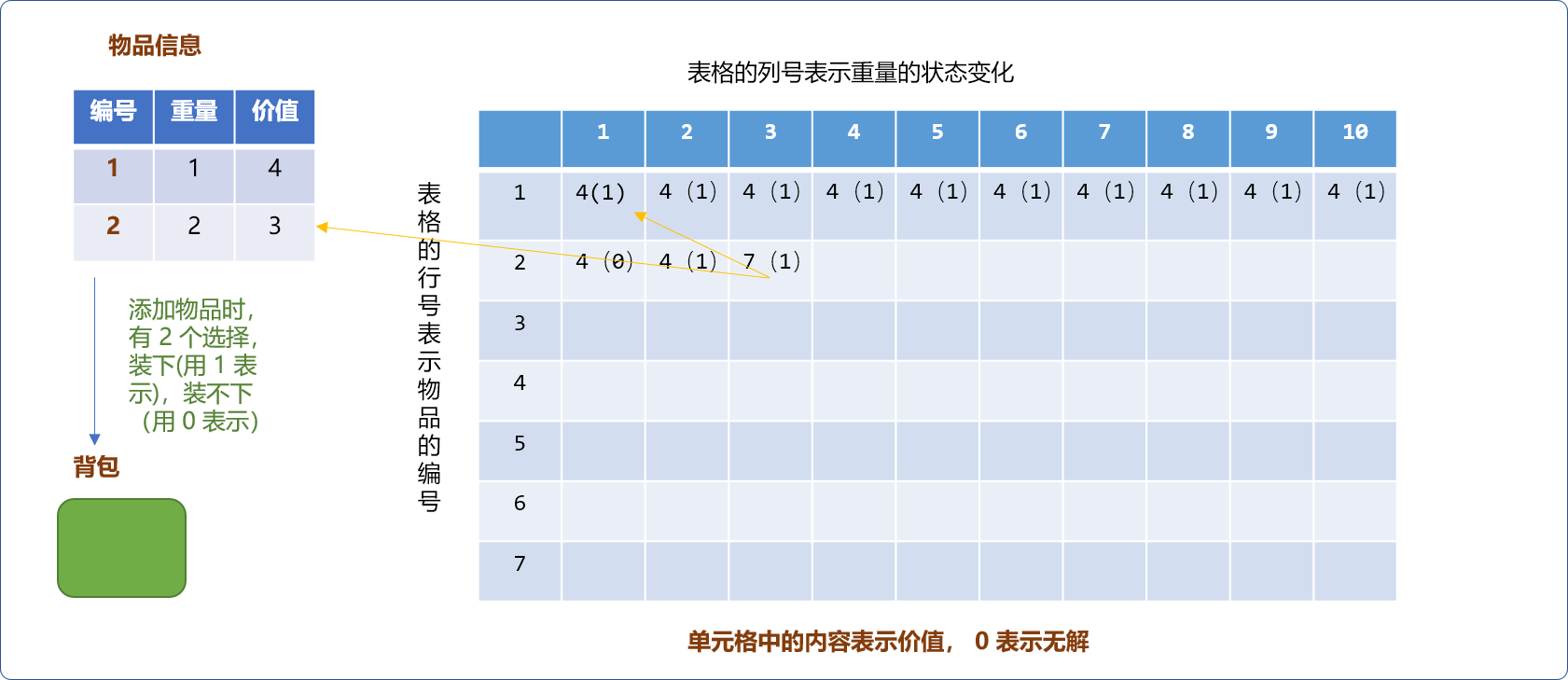
当背包容量是 3时，物品2也是可以放进去的。此时背包的价值可以是当前物品的价值 3加上背包剩余容量3-2=1能存放的最大价值4，计算后值为 7。要把此值和不把物品放进去时原来的价值 4 之间进行最大值选择。

dt25.png

所以，对于背包问题，核心思想就是：

  • 如果物品能放进背包：则先计算出物品的价值加上剩余容量能存储的最大价值之和，再找到不把物品放进背包时背包中原有价值。最后在两者之间进行最大值选择。
  • 当物品不能放进背包：显然，保留背包中原来的最大价值信息。

2.3.3 编码实现

#include <iostream>
#include <vector>
using namespace std;
int main(int argc, char** argv) {
	//物品信息
	int goods[3][3]= { {1,4},{2,3} };
	//背包容量
	int bagWeight=0;
	cout<<"请输入背包容量："<<endl;
	cin>>bagWeight;
	//状态表
	int db[4][bagWeight+1]= {0};
	for(int i=0; i<4; i++) {
		for(int j=0; j<bagWeight+1; j++) {
			db[i][j]=0;
		}
	}
	for(int w=1; w<4; w++) {
		for(int wt=1; wt<=bagWeight; wt++) {
			if( goods[w-1][0]>wt ) {
				//如果背包不能装下物品，保留背包上一次的结果
				db[w][wt]=db[w-1][wt];
			} else {
				//能装下,计算本物品价值和剩余容量的最大价值
				int val=goods[w-1][1] + db[w-1][ wt- goods[w-1][0] ];
				//背包原来的价值
				int val_= db[w-1][wt];
				//计算最大值
				db[w][wt]=val>val_?val:val_;
			}
		}
	}
	for(int i=1; i<3; i++) {
		for(int j=1; j<=bagWeight; j++) {
			cout<<db[i][j]<<"\t";
		}
		cout<<endl;
	}
	return 0;
}

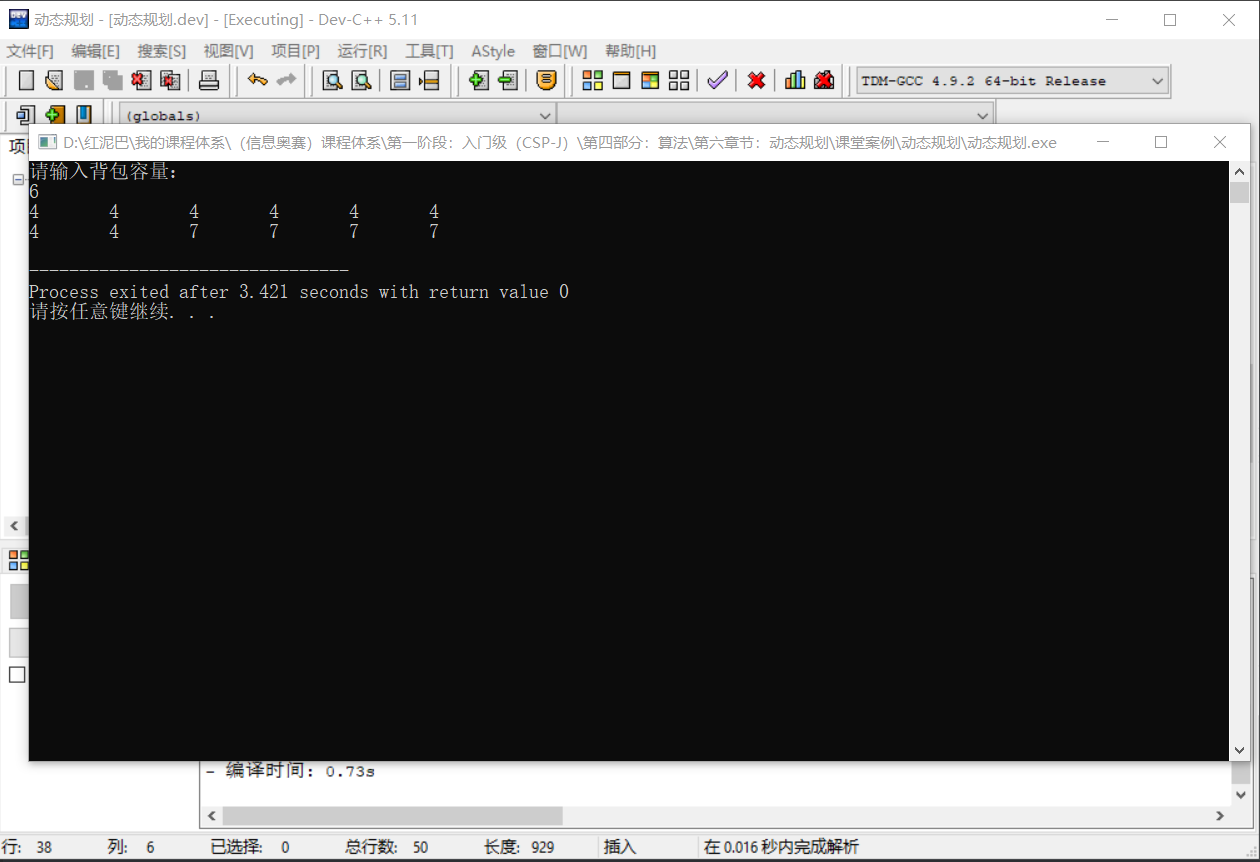
输出结果：

dt26.png

3. 总结

本文主要讲解背包系列 中的0-1背包问题。0-1背包问题可以使用递归和动态规划方案得到其解。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/395944.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何提高软件测试执行力

如何提高软件测试执行力

高效的测试执行力 不管在哪个行业&#xff0c;高校的执行力都是不可或缺的。在软件测试行业更是这样。有些测试人员&#xff0c;很勤奋也很吃苦&#xff0c;但是可能最终不能很好的完成测试任务。究其原因就是一个测试执行力的问题。 高效执行就是有目标&#xff0c;有计划&…
阅读更多...
BUUCTF [羊城杯 2020]easyre 题解

BUUCTF [羊城杯 2020]easyre 题解

一.查壳 64位无壳 二.主函数逻辑 可以得知flag长度为38,然后进行三次加密 第一次加密是base64加密,得到code1 第二次加密是将code1拆成四段赋给code2 第三次加密是将code2内的数字和字母移3位,其他字符不变 str2保存的是最终的加密字符 三.encode_one_base64 看到主函数…
阅读更多...
【Linux】Sudo的隐晦bug引发的一次业务问题排查

【Linux】Sudo的隐晦bug引发的一次业务问题排查

Sudo的隐晦bug引发的一次业务问题排查写在前面问题描述问题排查高负载现象排查日志排查跟踪任务调度过程Sudo引发的问题手动复现问题分析处理方案写在前面 记录一次生产环境sudo启动进程频繁被Kill且不报错的异常处理过程&#xff0c;如果遇到同样的问题只想要解决方案&#x…
阅读更多...
AWS攻略——初识流量镜像

AWS攻略——初识流量镜像

在实际应用场景下&#xff0c;我们可能需要建立一个测试环境&#xff0c;既能接线上流量&#xff0c;又不希望影响线上业务&#xff0c;这个时候流量镜像就派上用场。它会将一个网络接口中的流量复制到另外一个网络接口中&#xff0c;然后在后者上分发&#xff0c;而前者不受影…
阅读更多...
AQS 源码解读

AQS 源码解读

一、AQS AQS 是 AbstractQueuedSynchronizer 的简称&#xff0c;又称为同步阻塞队列&#xff0c;是 Java 中的一个抽象类。在其内部维护了一个由双向链表实现的 FIFO 线程等待队列&#xff0c;同时又提供和维护了一个共享资源 state &#xff0c;像我们平常使用的 ReentrantLo…
阅读更多...
OpenCV-PyQT项目实战（12）项目案例08：多线程视频播放

OpenCV-PyQT项目实战（12）项目案例08：多线程视频播放

欢迎关注『OpenCV-PyQT项目实战 Youcans』系列&#xff0c;持续更新中 OpenCV-PyQT项目实战&#xff08;1&#xff09;安装与环境配置 OpenCV-PyQT项目实战&#xff08;2&#xff09;QtDesigner 和 PyUIC 快速入门 OpenCV-PyQT项目实战&#xff08;3&#xff09;信号与槽机制 …
阅读更多...
配置Clion用于STM23开发（Makefile）

配置Clion用于STM23开发（Makefile）

前言 对于Clion配置STM32开发环境的教程在网上一搜一大堆&#xff0c;但是大部分都是22年之前的&#xff0c;使用的方法都是在STM32CubeMX生成SW4STM32工程。但是在22年不知道哪个版本后&#xff0c;CubeMX已经不再支持生成SW4STM32工程了&#xff0c;这也是我本人遇到的问题。…
阅读更多...
10 Wifi网络的封装

10 Wifi网络的封装

概述 Wifi有多种工作模式，比如：STA模式、AccessPoint模式、Monitor模式、Ad-hoc模式、Mesh模式等。但在IPC设备上，主要使用STA和AccessPoint这两种模式。下面分别进行介绍。 STA模式：任何一种无线网卡都可以运行在此模式，这种模式也是无线网卡的默认模式。在此模式下，无线…
阅读更多...
【算法】图的存储和遍历

【算法】图的存储和遍历

作者&#xff1a;指针不指南吗 专栏&#xff1a;算法篇 &#x1f43e;或许会很慢&#xff0c;但是不可以停下&#x1f43e; 文章目录1. 图的存储1.1 邻接矩阵1.2 邻接表2. 图的遍历2.1 dfs 遍历2.2 bfs 遍历1. 图的存储 引入 一般来说&#xff0c;树和图有两种存储方式&#…
阅读更多...
【Java】Mybatis查询数据库

【Java】Mybatis查询数据库

文章目录MyBatis查询数据库1. MyBatis 是什么&#xff1f;2. 为什么要学习MyBatis&#xff1f;3. 怎么学MyBatis&#xff1f;4. 第一个MyBatis查询4.1 创建数据库和表4.2 添加MyBatis框架支持4.3 配置连接字符串和MyBatis4.3.1 配置连接数据库配置MyBatis中的XML路径4.4 添加业…
阅读更多...
宝刀未老？VB语言迎来春天，低代码绝地逢生，程序员能淡定吗？

宝刀未老？VB语言迎来春天，低代码绝地逢生，程序员能淡定吗？

一、VB语言迎来春天 “VB语言过时了&#xff0c;早就淘汰了”&#xff0c;不少程序员认为&#xff0c;如今VB上不了台面。 有人说&#xff1a;VB是被微软砍掉的优秀产品之一&#xff0c;当年还和Delphi打对台来着, 那时候真的是如日中天&#xff01; 颠覆许多人认知的是28年过…
阅读更多...
postgre8.3跨平台升级大版本的一些问题以及解决方式

postgre8.3跨平台升级大版本的一些问题以及解决方式

背景&#xff1a; 因服务器升级&#xff08;Windows Server 2012-> 2019&#xff09;,服务器非直接版本升级&#xff0c;而是从一台2012直接移植到2019&#xff0c;考虑到以后可能还会升级更高版本&#xff0c;因此postgre8.3版本需要升级到新版本&#xff0c;当前时间postg…
阅读更多...
知识蒸馏论文阅读：DKD算法笔记

知识蒸馏论文阅读：DKD算法笔记

标题&#xff1a;Decoupled Knowledge Distillation 会议&#xff1a;CVPR2022 论文地址&#xff1a;https://ieeexplore.ieee.org/document/9879819/ 官方代码&#xff1a;https://github.com/megvii-research/mdistiller 作者单位&#xff1a;旷视科技、早稻田大学、清华大学…
阅读更多...
SpringCloud （Eureka服务注册、发现）

SpringCloud （Eureka服务注册、发现）

本章导学&#xff1a; 微服务各个服务如何调用&#xff1f;服务直接调用出现的问题Eureka的引出及其作用搭建单机Eureka 注册发现一、微服务各个服务之间的调用 很简单&#xff0c;我们只需要在SpringBoot的配置类里把RestTemplate类加载到容器&#xff0c;利用RestTemplate的…
阅读更多...
【目标检测 DETR】通俗理解 End-to-End Object Detection with Transformers，值得一品。

【目标检测 DETR】通俗理解 End-to-End Object Detection with Transformers，值得一品。

文章目录DETR1. 亮点工作1.1 E to E1.2 self-attention1.3 引入位置嵌入向量1.4 消除了候选框生成阶段2. Set Prediction2.1 N个对象2.2 Hungarian algorithm3. 实例剖析4. 代码4.1 配置文件4.1.1 数据集的类别数4.1.2 训练集和验证集的路径4.1.3 图片的大小4.1.4 训练时的批量…
阅读更多...
idea 2022.2.4 导入依赖警告的问题

idea 2022.2.4 导入依赖警告的问题

在我导入依赖的时候&#xff0c;pom文件提示警告如下信息 Provides transitive vulnerable dependency commons-collections:commons-collections:3.2.2 Cx78f40514-81ff 7.5 Uncontrolled Recursion vulnerability pending CVSS allocation Results powered by Checkmarx(c) …
阅读更多...
第十二章：网络编程

第十二章：网络编程

第十二章&#xff1a;网络编程 12.1&#xff1a;网络编程概述 ​ Java是Internet上的语言&#xff0c;它从语言级上提供了对网络应用程序的支持&#xff0c;程序员能够很容易开发常见的网络应用程序。 ​ Java提供的网络类库&#xff0c;可以实现无痛的网络连接&#xff0c;…
阅读更多...
【项目精选】基于struts+hibernate的采购管理系统

【项目精选】基于struts+hibernate的采购管理系统

点击下载 javaEE采购管理系统 本系统是一个独立的系统&#xff0c;用来解决企业采购信息的管理问题。采用JSP技术构建了一个有效而且实用的企业采购信息管理平台&#xff0c;目的是为高效地完成对企业采购信息的管理。经过 对课题的深入分析&#xff0c;采购系统需实现以下功能…
阅读更多...
秒懂算法 | DP概述和常见DP面试题

秒懂算法 | DP概述和常见DP面试题

动态（DP）是一种算法技术，它将大问题分解为更简单的子问题，对整体问题的最优解决方案取决于子问题的最优解决方案。本篇内容介绍了DP的概念和基本操作；DP的设计、方程推导、记忆化编码、递推编码、滚动数组以及常见的DP面试题。 01、DP概述 1. DP问题的特征 下面以斐波那…
阅读更多...
在找docker命令和部署？看这一篇文章就够了。

在找docker命令和部署？看这一篇文章就够了。

一、docker 常用命令 docker ps -a #查看所有容器 docker images #查看所有images docker search rabbitmq #搜索rabbitmq docker pull rabbitmq #拉去rabbitmq docker run -id --namemy_rabbitmq -p 5672:5672 -p 15672:15672 rabbitmq # 创建一个容器并启动 docker exec -it…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023