作者:指针不指南吗
专栏:算法篇🐾或许会很慢,但是不可以停下🐾
文章目录
- 1. 图的存储
- 1.1 邻接矩阵
- 1.2 邻接表
- 2. 图的遍历
- 2.1 dfs 遍历
- 2.2 bfs 遍历
1. 图的存储
- 引入
一般来说,树和图有两种存储方式,树是无环连通图,树是特殊的图,这里只讲图。
图分成两种有向图和无向图
无向图:有向图建两条边,a->b , b->a
所以说,无向图是一种特殊的有向图 , 我们只讲 有向图的存储
1.1 邻接矩阵
二维数组, g[a][b] ,a 到 b 的边
比较浪费空间,适合存储 稠密图,用的比较少
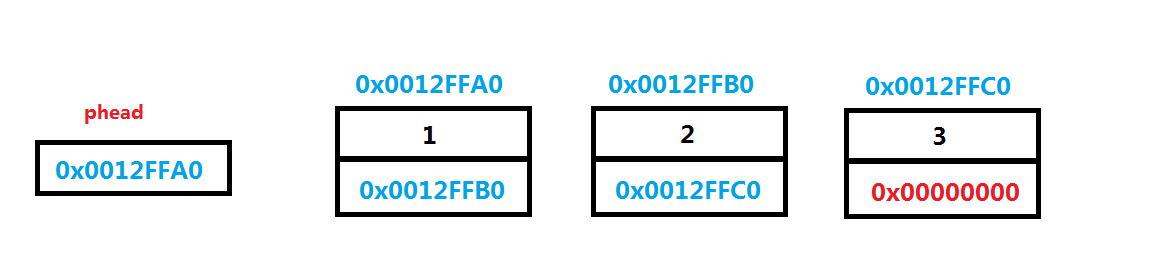
1.2 邻接表
图和部分注释转自 acwing
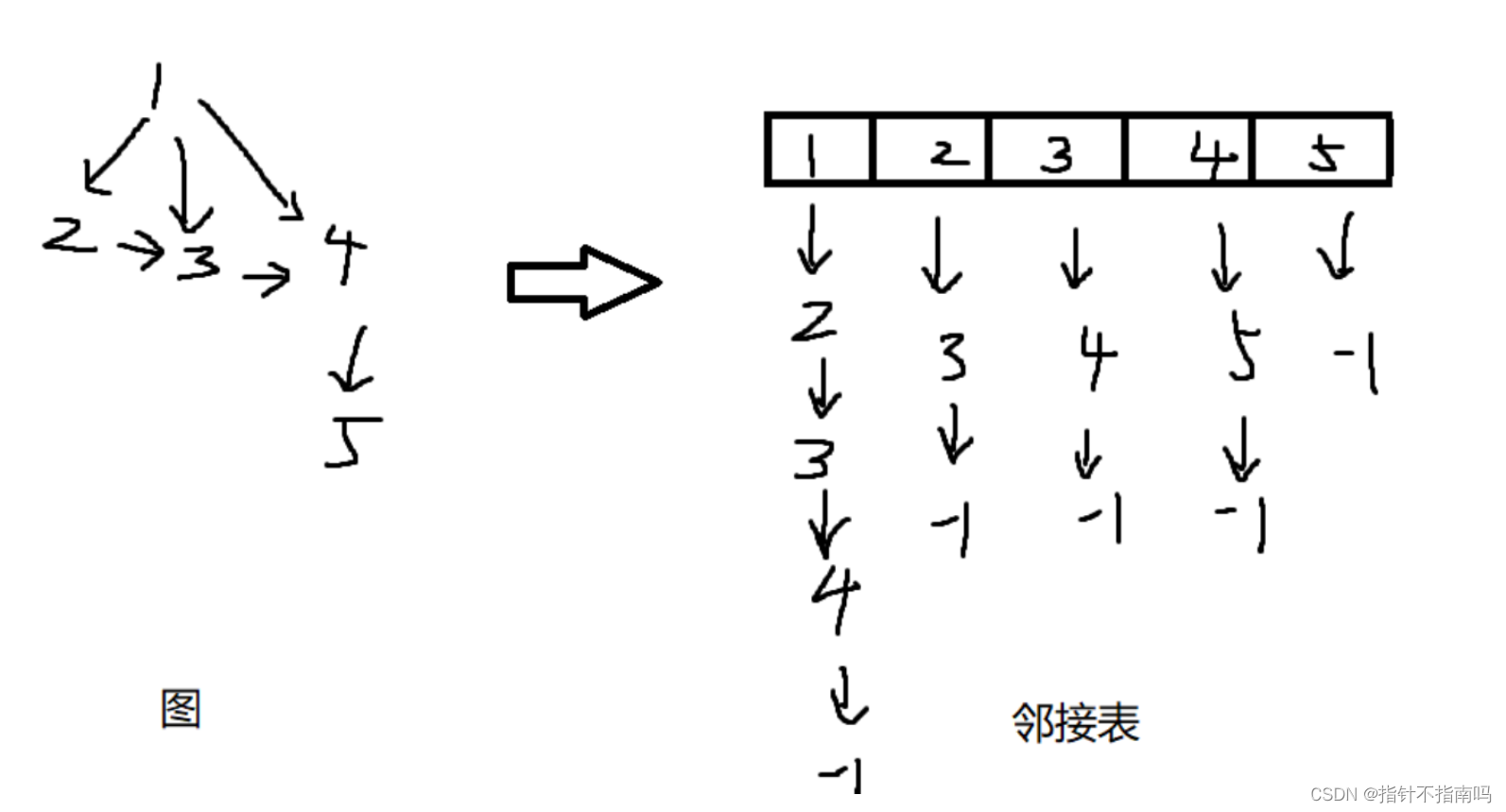
- 代码实现
#include<bits/stdc++.h>
using namespace std;
//N : 节点数量
//M:边的数量
//i : 节点的下标索引
//idx : 边的下标索引
const int N=100010,M=2*N;
//h[N] : 表示 第 i 个节点的 第一条边的 idx
//ne[M] : 表示 与 第 idx 条边 同起点 的 下一条边 的 idx
//e[M] : 表示 第idx 条边的 终点 表示值
int h[N],e[M],ne[M],idx;
void add(int a, int b) //插入一个 a->b 的边
{
e[idx]=b; // 记录 加入的边 的终点节点, 记录值
h[idx]=h[a]; // h[a] 表示 节点 a 为起点的第一条边的下标,ne[idx] = h[a] 表示把 h[a] 这条边接在了 idx 这条边的后面,其实也就是把 a 节点的整条链表 接在了 idx 这条边 后面;目的就是为了下一步 把 idx 这条边 当成 a 节点的单链表的 第一条边,完成把最新的一条边插入到 链表头的操作;
h[a]=idx++; a节点开头的第一条边置为当前边,idx移动到下一条边
}
int main()
{
int n;
cin>>n;
memset(h,-1,sizeof h); //把每个头节点 初始化为 -1
return 0;
}
2. 图的遍历
一般我们每个元素就遍历一次
两种搜索方式,每个点只遍历一次:深搜一边路走到黑 ;宽搜 一层一层的搜
边的权重 都相等,则使用 bfs 找最短路
2.1 dfs 遍历
- 代码模板
#include<bits/stdc++.h>
using namespace std;
const int N=100010,M=N*2; //以有向图的格式存储无向图,所以每个节点至多对应2n-2条边
int n;
int h[N],e[M],ne[M],idx;
bool st[N];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
// 树 dfs 遍历 框架
void dfs(int u) //遍历以 u 为根节点的子树
{
if(u==n) return ; //边界条件就是左右的点 都遍历过了
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i]; // 去出当前节点编号
if(!st[j]) //没有使用过,继续
{
st[j]=true; //改变状态
dfs(j); //dfs 下一个节点,就是搜索以 j 为根节点的子树
}
}
}
int main()
{
cin>>n;
memset(h,-1,sizeof h); //给头节点 初始化
return 0;
}
-
例题
链接:[acwing 846.树的重心]( 846. 树的重心 - AcWing题库 )
给定一颗树,树中包含 n 个结点(编号 1∼n)和 n−1 条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式
第一行包含整数 n,表示树的结点数。
接下来 n−1 行,每行包含两个整数 a 和 b,表示点 a 和点 b 之间存在一条边。
输出格式
输出一个整数 m,表示将重心删除后,剩余各个连通块中点数的最大值。
数据范围
1≤n≤ 1 0 5 10^5 105
输入样例:
9 1 2 1 7 1 4 2 8 2 5 4 3 3 9 4 6输出样例:
4 -
思路
-
把树存在邻接表里面
-
开始找去除重心之后,使剩余几部分连通图中,每一部分节点最大数量 最小
- 我们可以通过 dfs ,找到每个子树中节点数量
- 算出一个子树的每一部分 ABC , 取他们的 最 max ,计算每一个节点的这几个部分
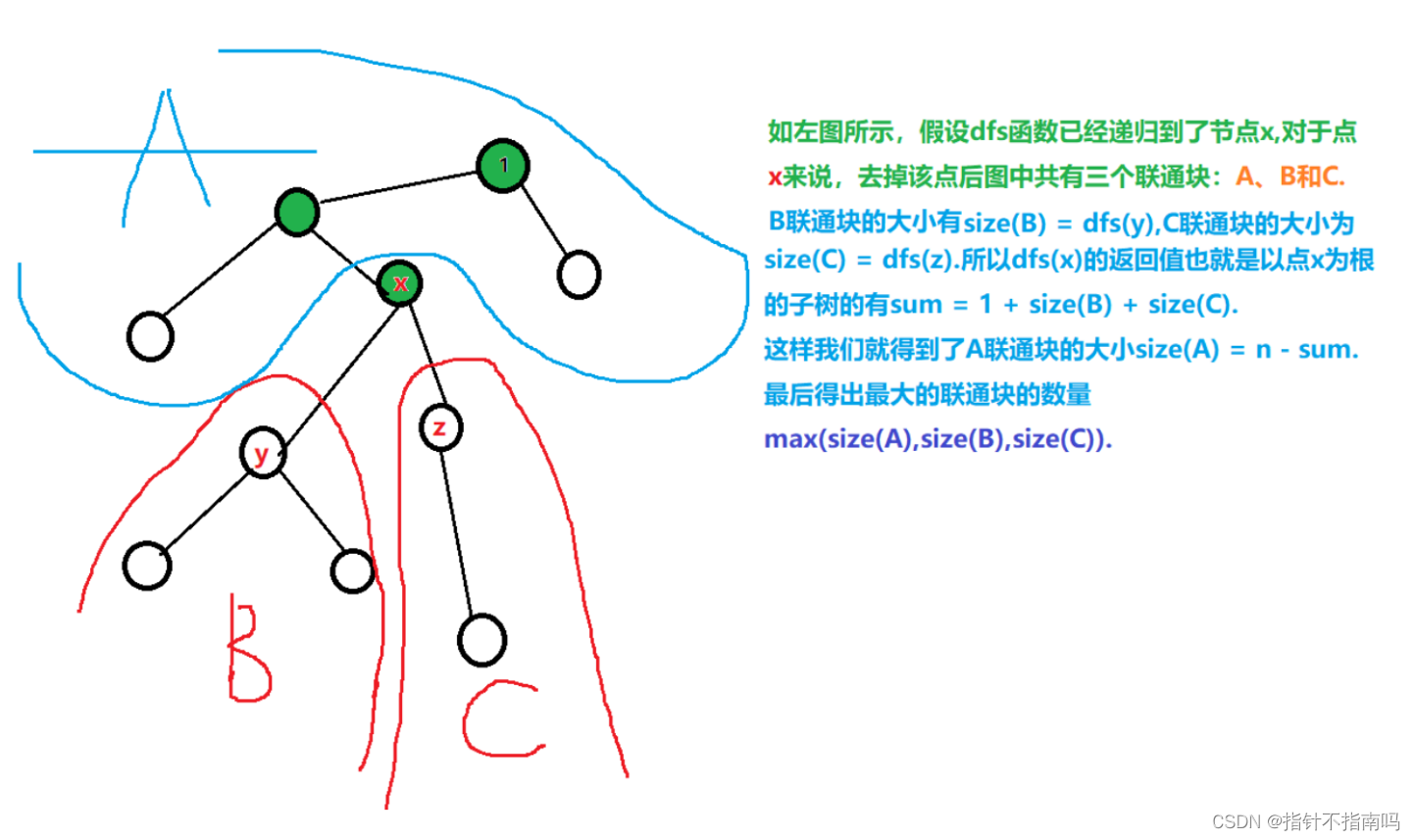
-
-
代码实现
#include<bits/stdc++.h> using namespace std; const int N=1e5+10,M=2*N; int n; int h[N],e[M],ne[M],idx; int ans=N; //最小值,初始化为 一个最大数 bool st[N]; void add(int a,int b) { e[idx]=b,ne[idx]=h[a],h[a]=idx++; } int dfs(int u) //返回的是,去除 u 节点之后最大连通图的数量 { st[u]=true; //改变状态 //size 表示子树连通块中点的数量(图中 B或者C) //sum 表示以 u 为根节点所有的子树点的数量(图中 x点+B+C) int size=0,sum=1; for(int i=h[u];i!=-1;i=ne[i]) //遍历以 u 为根节点的子树 { int j=e[i]; //j 表示现在正在遍历的节点编号 if (st[j]) continue; //遍历过了,跳过进行下一个 st[j]=true; //改变状态 int s=dfs(j); //存的是,以 j 为根节点的所有子树的中点的数量 size=max(size,s); //取所有 子树中点数量最大的值 相当于比较图中的B,C sum+=s; //sum+ 扩展的子树中点的数量 } size=max(size,n-sum); //相当于比较途中 各个部分 ABC 的最大值 ans=min(size,ans); //取最大值的最小值 return sum; //返回 以 u 为根节点的所有子树地最大值 } int main() { cin>>n; memset(h,-1,sizeof h); for(int i=0;i<n;i++) { int a,b; cin>>a>>b; add(a,b),add(b,a); //注意这里是 无向图,有两条边 } dfs(1); //开始遍历树 cout<<ans; //输出结果 return 0; }
2.2 bfs 遍历
- 代码模板
//宽搜框架
queue<int > q;
q.push(1); //把编号 1 节点放进去
while(!q.empty())
{
int t=q.front();
q.pop();
//拓展所有t可以到的节点,邻点
if(/*邻点x没有被遍历过*/)
{
q.push(x);
st[x]=1;
d[x]=d[t]+1;
}
}
-
例题
链接: 847. 图中点的层次 - AcWing题库
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环。
所有边的长度都是 1,点的编号为 1∼n。
请你求出 1 号点到 n 号点的最短距离,如果从 1号点无法走到 n 号点,输出 −1。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 a 和 b,表示存在一条从 a 走到 b 的长度为 1 的边。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
数据范围
1≤n,m≤ 1 0 5 10^5 105
输入样例:
4 5 1 2 2 3 3 4 1 3 1 4输出样例:
1 -
思路
我们第一发现这个点,就是源点到这个点的最短路径
首先判断出来 这道题是使用 bfs
然后 , 图的存储, 图的遍历 模板题
-
代码实现
#include<bits/stdc++.h> using namespace std; const int N=1e5+10,M=N*2; int n,m; //n表示点,m表示边 int h[N],e[M],ne[M],idx; bool st[N]; int q[N],d[N]; //q表示队列,d表示距离 void add(int a,int b) { e[idx]=b,ne[idx]=h[a],h[a]=idx++; } int bfs() { int hh,tt; //hh表示队头,tt表示队尾 q[0]=1; //存储层次遍历序列 0号节点是编号为1的节点 memset(d,-1,sizeof d); //d[]==-1,表示没有被遍历过 d[1]=0; //储存每个节点到 起点 编号1 的距离 while(hh<=tt) { //取出 队头 int t=q[hh++]; //遍历t节点的每一个邻边 for(int i=h[t];i!=-1;i=ne[i]) { int j=e[i]; if(d[j]==-1) //j 没有没被扩展过 { d[j]=d[t]+1; //该点的距离+1,并且表示已经被扩展过了 q[++tt]=j; //把扩展的点放到队列里面去,压入队列 } } } return d[n]; //返回编号为 n 的节点到 起点的距离 } int main() { cin>>n>>m; memset(h,-1,sizeof h); for(int i=0;i<m;i++) //读入边 { int a,b; cin>>a>>b; add(a,b); } cout<<bfs(); return 0; }STL 队列实现 bfsint bfs() { queue<int> q; q.push(1); // q[0]=1; //存储层次遍历序列 0号节点是编号为1的节点 memset(d,-1,sizeof d); //d[]==-1,表示没有被遍历过 d[1]=0; //储存每个节点到 起点 编号1 的距离 while(!q.empty()) { int t=q.front(); q.pop(); for(int i=h[t];i!=-1;i=ne[i]) { int j=e[i]; if(d[j]==-1) { d[j]=d[t]+1; q.push(j); } } } }










![[ 网络 ] 应用层协议——HTTPS协议原理](https://img-blog.csdnimg.cn/1b0c65e1b4354dbd982171688df65d9e.png)