蓝桥杯集训每日一题acwing3305

作物杂交是作物栽培中重要的一步。

已知有 N 种作物 (编号 1 至 N)，第 i 种作物从播种到成熟的时间为 Ti。

作物之间两两可以进行杂交，杂交时间取两种中时间较长的一方。

如作物 A 种植时间为 5 天，作物 B 种植时间为 7 天，则 AB 杂交花费的时间为 7 天。

作物杂交会产生固定的作物，新产生的作物仍然属于 N 种作物中的一种。

初始时，拥有其中 M 种作物的种子 (数量无限，可以支持多次杂交)。

同时可以进行多个杂交过程。

求问对于给定的目标种子，最少需要多少天能够得到。

如存在 4 种作物 ABCD，各自的成熟时间为 5 天、7 天、3 天、8 天。

初始拥有 AB 两种作物的种子，目标种子为 D，已知杂交情况为 A×B→C，A×C→D。

则最短的杂交过程为：

第 1 天到第 7 天 (作物 B 的时间)，A×B→C。

第 8 天到第 12 天 (作物 A 的时间)，A×C→D。

花费 12 天得到作物 D 的种子。

输入格式

输入的第 1 行包含 4 个整数 N,M,K,T，N 表示作物种类总数 (编号 1 至 N)，M 表示初始拥有的作物种子类型数量，K 表示可以杂交的方案数，T 表示目标种子的编号。

第 2 行包含 N 个整数，其中第 i 个整数表示第 i 种作物的种植时间 Ti。

第 3 行包含 M 个整数，分别表示已拥有的种子类型 Kj，Kj 两两不同。

第 4 至 K+3 行，每行包含 3 个整数 A,B,C，表示第 A类作物和第 B 类作物杂交可以获得第 C� 类作物的种子。

输出格式

输出一个整数，表示得到目标种子的最短杂交时间。

样例解释

1≤N≤2000,
2≤M≤N,
1≤K≤10^5,
1≤T≤N,
1≤Ti≤100,
1≤Kj≤M,
保证目标种子一定可以通过杂交得到。
不保证作物 A 和 B 杂交只能生成作物 C（也就是说，A×B→C 和 A×B→D 可能同时在输入中出现）
不保证作物 C 只能由作物 A 和 B 杂交生成（也就是说，A×B→D 和 A×C→D 可能同时在输入中出现）。
不保证同一杂交公式不在输入中重复出现。

输入样例：

6 2 4 6
5 3 4 6 4 9
1 2
1 2 3
1 3 4
2 3 5
4 5 6

输出样例：

16

样例解释

第 1 天至第 5 天，将编号 1 与编号 2 的作物杂交，得到编号 3 的作物种子。

第 6 天至第 10 天，将编号 1 与编号 3 的作物杂交，得到编号 4 的作物种子。

第 6 天至第 9 天，将编号 2 与编号 3 的作物杂交，得到编号 5 的作物种子。

第 11 天至第 16 天，将编号 4 与编号 5 的作物杂交，得到编号 6 的作物种子。

总共花费 16 天。

 

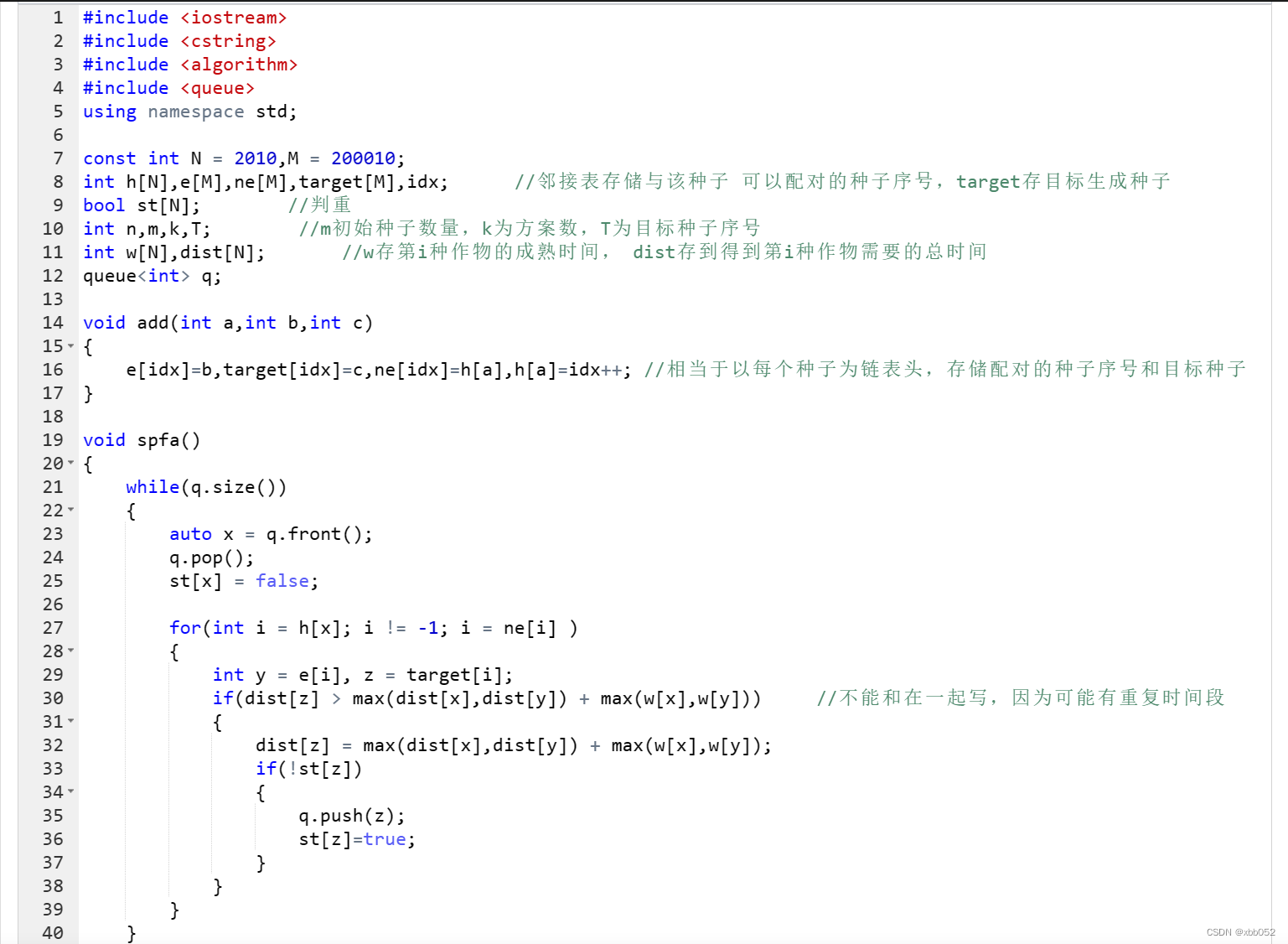
 考虑动态规划，属性是求最小花费时间。

采用的数据存储结构是邻接表，这里相当于对每一个种子都开一个链表，以该种子为表头，存储与该种子配对杂交的种子，以及生成的目标种子

dist数组存储得到第i个种子所花费的总时长

所以当用spfa（）算法求时长时，动态转移方程为：

假设 x  杂交  y  ------>    Z             则有dist [ Z ]  = max( dist[ x ] , dist[ y ] ) +max( w[ x ] , w[ y ] ) ;

不写成max(dist[x] + w[x] ,dist[y] + w[y]),因为当中可能有重复的时间段无法计算到

接下来看代码解析: