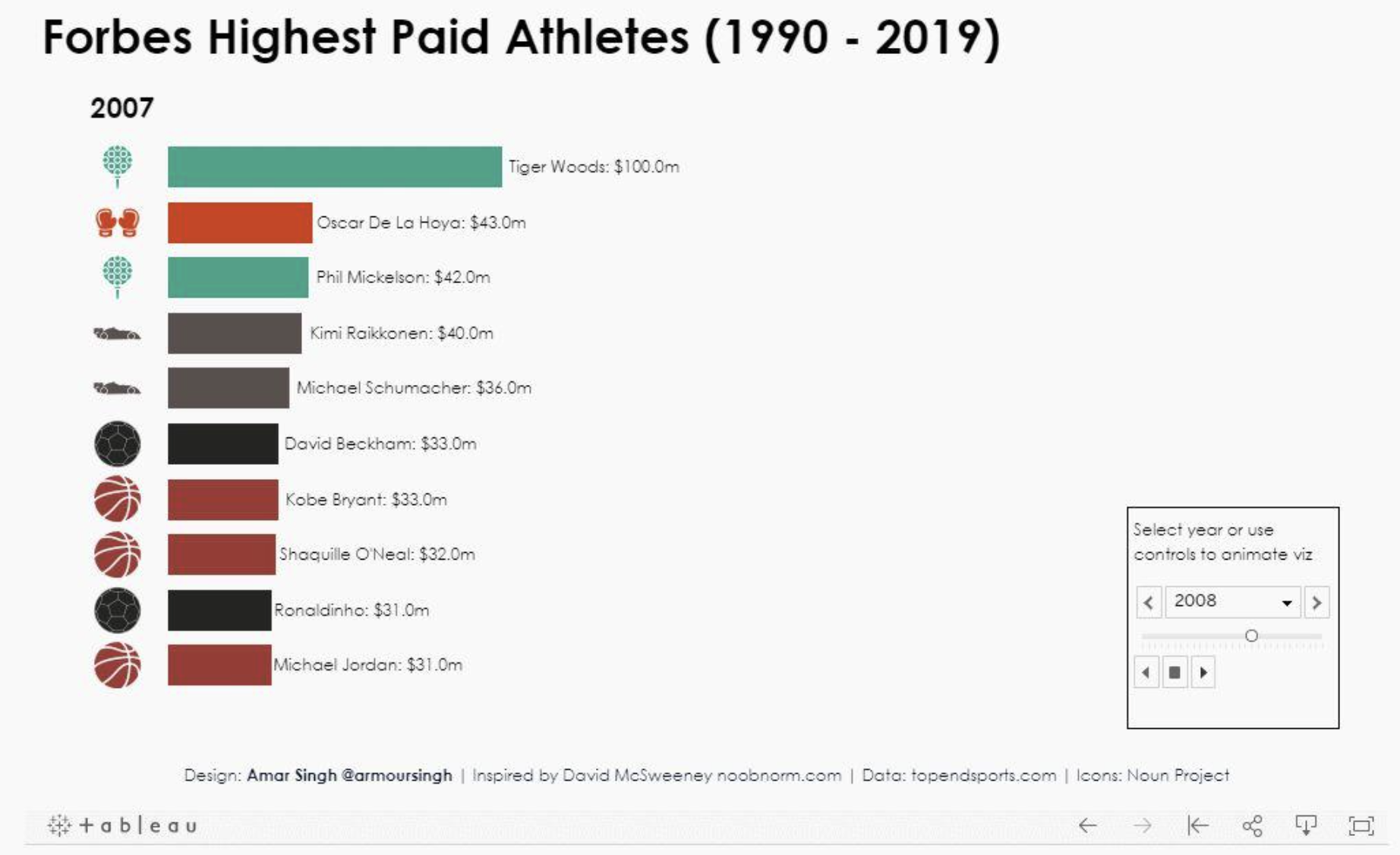
矩阵乘法是线性代数中最常见的问题之一,在数值计算中有广泛的应用。设4和B是两
个nxn矩阵,它们的乘积 AB 同样是一个nxn矩阵。A和B的乘积矩阵 C中元素C定义为
C =2anw6o
=1
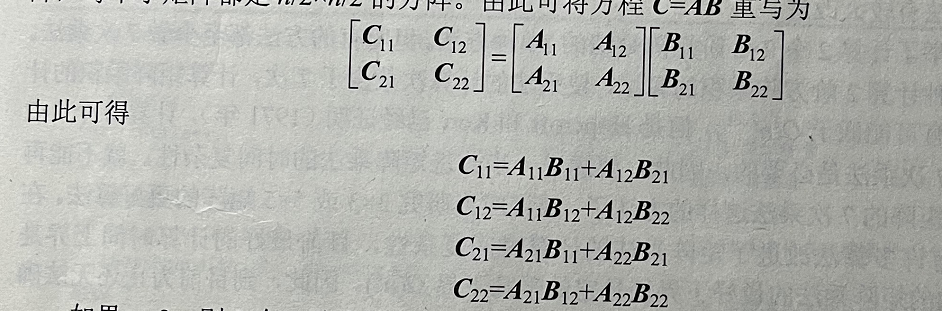
若依此定义来计算4 和B的乘积短阵C,则每计算 C的一个元素C,需要做n次乘法
和1-1 次加法。因此,求出矩阵C的八个元素所需的计算时间为 O((n)。
20 世纪 60年代末,Strassen 采用子类似于在大整数乘法中用过的分治技术,将计算 2
个n阶矩阵乘积所需的计算时间改进到 0(1083=0(n2.81。其基本思想还是使用分治法。
首先,仍假设n是2的幂。将矩阵4 、B和C中每个矩阵都分块成 4个大小相等的子矩
阵,每个子矩阵都是 n/2xn1/2 的方阵。由此可将方程C=4B 重写为
如果1=2,则2个2阶方阵的乘积可以直接计算出来,共需8次乘法和4 次加法。当子
矩阵的阶大于2时,为求2个子矩阵的积,可以继续将子矩阵分块,直到子矩阵的阶降为 2。
由此产生了分治降阶的递归算法。依此算法,计算2个n阶方阵的乘积转化为计算8个n/2
阶方阵的乘积和4个n/2阶方阵的加法。2个n/2xn/2矩阵的加法显然可以在 O(n时间内完
成。因此,上述分治法的计算时间耗费 T(n)应满足
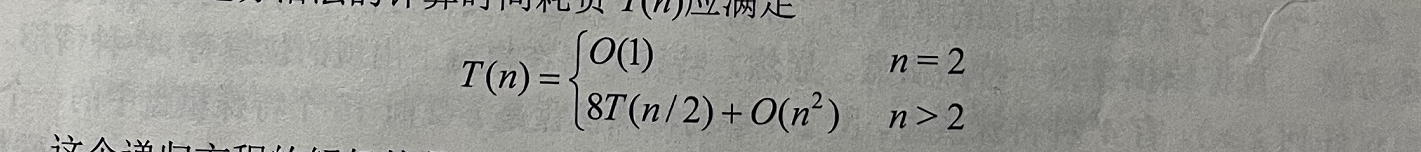
这个递归方程的解仍然是 7n=0()。因此,该方法并不比用原始定义直接计算更有效。
究其原因,是由于该方法并没有减少矩阵的乘法次数。而矩阵乘法耗费的时间要比矩阵加
(减)法耗费的时间多得多,要想改进矩阵乘法的计算时问复杂性,必须减少乘法运算。
按照上达分治法的思想可以看出,要想减少乘法运算次数,关键在于计算2个2阶方阵
的乘积时,能否用少于8次的乘法运算。Strassen 提出了一种新的算法来计算2个2阶方阵
的乘积。该算法只用了 7次乘法运算,但增加了加减法的运算次数。这7次乘法是
019

以上计算的正确性容易验证。
Strassern 短阵乘法中用了7 次对于n/2 阶矩阵乘积的递归调用和 18 次11/2 阶矩阵的加
运算。由此可知,该算法所需的计算时间T(n满足如下递归方程:
O(1)
n=2
T(n) =
177(1/2)+0() n>2
解此递归方程得 70=0(11087~0(72.81)。由此可见, Strassen 矩阵乘法的计算时间复杂性
比普通矩阵乘法有较大改进。
有人曾列举了计算2个2×2阶矩阵乘法的36种方法。但所有的方法都至少做7 次乘法
除非能找到一种计算2阶方阵乘积的算法,使乘法的计算次数少于7次,计算矩阵乘积的计
算时间下界才有可能低于 0(n?.81。但是Hopcrof 和Kerr 己经证明(1971年),计算2个2x2
矩阵的乘积,7 次乘法是必要的。因此,要想进一步改进矩阵乘法的时间复杂性,就不能再
基于计算 2x2矩阵的7 次乘法这样的方法了,或许应当研究 3x3 或 5x5 矩阵的更好算法。在
Strassen 之后有许多算法改进了矩阵乘法的计算时间复杂性,目前最好的计算时间上界是
0(02-376),所知的矩阵乘法的最好下界仍是它的平凡下界2(n。因此,到目前为止还无法确
切知道矩阵乘法的时间复杂性。关于这一研究课题还有许多工作可做。