目录
- 概述
- sin函数例子
- 四则运算
- 实数
- 复数
- 逻辑运算
- 复数运算
- 模
- 幅角
- 共轭
- 向量
- 二维向量定义
- 序列生成向量
- 向量索引方式
- 加减乘除
- 向量间运算
- 加减
- 乘法
- 除法
概述
MATLAB是美国MathWorks公司出品的商业数学软件,用于数据分析、无线通信、深度学习、图像处理与计算机视觉、信号处理、量化金融与风险管理、机器人,控制系统等领域。 [1]
MATLAB是matrix&laboratory两个词的组合,意为矩阵工厂(矩阵实验室),软件主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式。
sin函数例子
>> x=1:0.1:10
x =
列 1 至 13
1.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000 1.7000 1.8000 1.9000 2.0000 2.1000 2.2000
列 14 至 26
2.3000 2.4000 2.5000 2.6000 2.7000 2.8000 2.9000 3.0000 3.1000 3.2000 3.3000 3.4000 3.5000
列 27 至 39
3.6000 3.7000 3.8000 3.9000 4.0000 4.1000 4.2000 4.3000 4.4000 4.5000 4.6000 4.7000 4.8000
列 40 至 52
4.9000 5.0000 5.1000 5.2000 5.3000 5.4000 5.5000 5.6000 5.7000 5.8000 5.9000 6.0000 6.1000
列 53 至 65
6.2000 6.3000 6.4000 6.5000 6.6000 6.7000 6.8000 6.9000 7.0000 7.1000 7.2000 7.3000 7.4000
列 66 至 78
7.5000 7.6000 7.7000 7.8000 7.9000 8.0000 8.1000 8.2000 8.3000 8.4000 8.5000 8.6000 8.7000
列 79 至 91
8.8000 8.9000 9.0000 9.1000 9.2000 9.3000 9.4000 9.5000 9.6000 9.7000 9.8000 9.9000 10.0000
>> y=sin(x)
y =
列 1 至 13
0.8415 0.8912 0.9320 0.9636 0.9854 0.9975 0.9996 0.9917 0.9738 0.9463 0.9093 0.8632 0.8085
列 14 至 26
0.7457 0.6755 0.5985 0.5155 0.4274 0.3350 0.2392 0.1411 0.0416 -0.0584 -0.1577 -0.2555 -0.3508
列 27 至 39
-0.4425 -0.5298 -0.6119 -0.6878 -0.7568 -0.8183 -0.8716 -0.9162 -0.9516 -0.9775 -0.9937 -0.9999 -0.9962
列 40 至 52
-0.9825 -0.9589 -0.9258 -0.8835 -0.8323 -0.7728 -0.7055 -0.6313 -0.5507 -0.4646 -0.3739 -0.2794 -0.1822
列 53 至 65
-0.0831 0.0168 0.1165 0.2151 0.3115 0.4048 0.4941 0.5784 0.6570 0.7290 0.7937 0.8504 0.8987
列 66 至 78
0.9380 0.9679 0.9882 0.9985 0.9989 0.9894 0.9699 0.9407 0.9022 0.8546 0.7985 0.7344 0.6630
列 79 至 91
0.5849 0.5010 0.4121 0.3191 0.2229 0.1245 0.0248 -0.0752 -0.1743 -0.2718 -0.3665 -0.4575 -0.5440
>> plot(x,y)
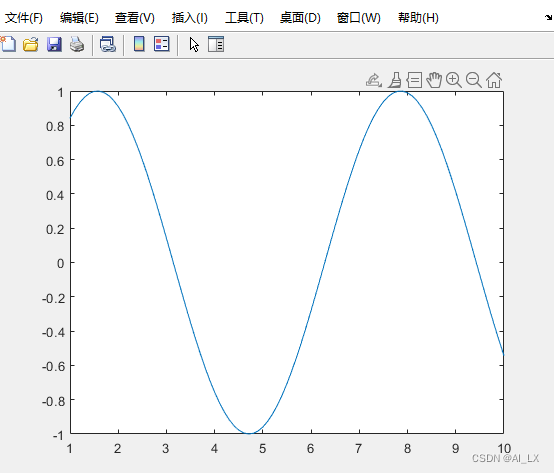
四则运算
实数
>> x=[1 2 3]
x =
1 2 3
>> x*2
ans =
2 4 6
>> x+6
ans =
7 8 9
>> x-9
ans =
-8 -7 -6
>> x/3
ans =
0.3333 0.6667 1.0000
>>
复数
>> x=11+9i
x =
11.0000 + 9.0000i
>> y=9-6i
y =
9.0000 - 6.0000i
>> x-y
ans =
2.0000 +15.0000i
>> x+y
ans =
20.0000 + 3.0000i
>> x*y
ans =
1.5300e+02 + 1.5000e+01i
>> y/x
ans =
0.2228 - 0.7277i
>>
逻辑运算
>> %逻辑与,两个操作数同时为1时,结果为1,否则为0
>> and(11,0)
ans =
logical
0
>> and(-11,0)
ans =
logical
0
>> %逻辑或,两个操作其中至少一个为1时,结果为1,否则为0
>> or(11,0)
ans =
logical
1
>> or(-11,0)
ans =
logical
1
>> or(0,0)
ans =
logical
0
>>
>>> %逻辑非,当操作数为0时,结果为1,否则为0
>> ~ 11
ans =
logical
0
>> ~ 0
ans =
logical
1
>>
>>> %逻辑异或,相同时为0,不同时为1
>> xor(0,1)
ans =
logical
1
>> xor(11,11)
ans =
logical
0
>>
>>> %有非零元素为真,为1,否则为0
>> any([11 22 0 -11])
ans =
logical
1
>> any([0 0 0 0])
ans =
logical
0
>>
>>> %所有元素非零为真,为1,否则为0
>> all([11,22,44,0])
ans =
logical
0
>> all([11,22,0,0])
ans =
logical
0
>> all([11,22,10,110])
ans =
logical
1
>>
%表示注释
复数运算
>> a=12-9i
a =
12.0000 - 9.0000i
或者下面这种方式定义
>> complex(12,-9)
ans =
12.0000 - 9.0000i
模
>> abs(a)
ans =
15
幅角
>> angle(a)
ans =
-0.6435
>>
共轭
实数部分
>> real(a)
ans =
12
虚数部分
>> imag(a)
ans =
-9
共轭复数
>> conj(a)
ans =
12.0000 + 9.0000i
如果单个复数或复数矩阵中的虚部为0,则为实数矩阵
>> a=11-9i
a =
11.0000 - 9.0000i
>> b=9+0i
b =
9
>> c=0-1i
c =
0.0000 - 1.0000i
>> isreal(a)
ans =
logical
0
>> isreal(b)
ans =
logical
1
>> isreal(c)
ans =
logical
0
向量
二维向量定义
>> x=[1,2;3,4]
x =
1 2
3 4
>> x=[1 2; 3 4]
x =
1 2
3 4
序列生成向量
>> x=[1:10]
x =
1 2 3 4 5 6 7 8 9 10
>> x=[1:3:12]%相差3生成序列
x =
1 4 7 10
>> x=linspace(1,10,3)%定义元素个数,linspace(第一个元素,最后一个元素,元素个数)
x =
1.0000 5.5000 10.0000
>> x=logspace(1,5,3)%定义元素个数,linspace(a,b,元素个数),10^a为第一个元素,10^b为最后一个元素
x =
10 1000 100000
>> x
x =
10 1000 100000
向量索引方式
注意从1开始,不从0开始。
>> x(1)
ans =
10
>> x(1:2)
ans =
10 1000
>> x(2:3)
ans =
1000 100000
>> x(0)
数组索引必须为正整数或逻辑值。
加减乘除
每个元素进行
>> x=linspace(1,12,4)
x =
1.0000 4.6667 8.3333 12.0000
>> y=linspace(3,15,4)
y =
3 7 11 15
>> x/2
ans =
0.5000 2.3333 4.1667 6.0000
>> x*2
ans =
2.0000 9.3333 16.6667 24.0000
>> x+2
ans =
3.0000 6.6667 10.3333 14.0000
>> x-2
ans =
-1.0000 2.6667 6.3333 10.0000
向量间运算
加减
每个对应元素进行
>> x
x =
1.0000 4.6667 8.3333 12.0000
>> y
y =
3 7 11 15
>> x+y
ans =
4.0000 11.6667 19.3333 27.0000
>> x-y
ans =
-2.0000 -2.3333 -2.6667 -3.0000
乘法
1、向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。
两个向量a和b的叉积写作a×b
向量积可以被定义为:
模长:(在这里θ表示两向量之间的夹角(共起点的前提下)(0°≤θ≤180°),它位于这两个矢量所定义的平面上。)
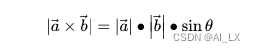
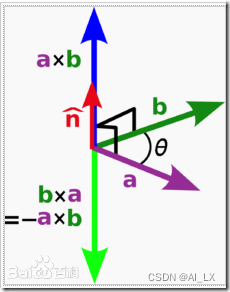
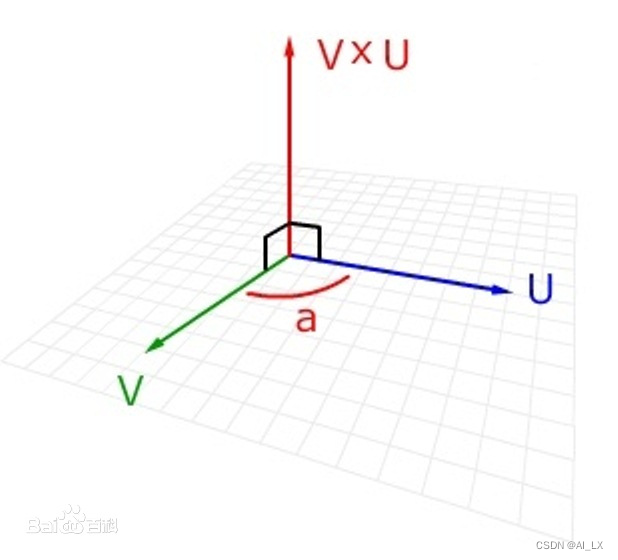
方向:a向量与b向量的向量积的方向与这两个向量所在平面垂直,且遵守右手定则。c的方向垂直于a与b所决定的平面,c的指向按右手定则从a转向b来确定。
>> x
x =
1 3 5
>> y
y =
10 12 14
>> cross(x,y)
ans =
-18 36 -18
2、点积
点积在数学中,又称数量积(dot product; scalar product),是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。


>> x
x =
1.0000 4.6667 8.3333 12.0000
>> y'
ans =
3
7
11
15
>> x*y'
ans =
307.3333
>> x=[1:2:6]
x =
1 3 5
>> y=[10:2:15]
y =
10 12 14
>> dot(x,y)
ans =
116
>> x*y'
ans =
116
3、点乘与点除
每个元素进行
>> x
x =
1 3 5
>> y
y =
10 12 14
>> x.*y
ans =
10 36 70
>> y./x
ans =
10.0000 4.0000 2.8000
除法
在两个向量平行时才有除法
>> x=[1 4]
x =
1 4
>> y=[6 24]
y =
6 24
>> y/x
ans =
6
>> x/y
ans =
0.1667
cross
叉积
语法
matlab C = cross(A,B) C = cross(A,B,dim)说明
C = cross(A,B)返回 A 和 B 的叉积。如果 A 和 B 为向量,则它们的长度必须为 3。
如果 A 和 B 为矩阵或多维数组,则它们必须具有相同大小。在这种情况下,cross 函数将 A 和 B 视为三元素向量集合。该函数计算对应向量沿大小等于 3 的第一个数组维度的叉积。
C = cross(A,B,dim)计算数组 A 和 B 沿维度 dim 的叉积。A 和 B 必须具有相同的大小,并且 size(A,dim) 和 size(B,dim) 必须为 3。dim 输入是一个正整数标量。
dim - 沿其运算的维度
正整数标量
沿其运算的维度,指定为正整数标量。维度 dim 的大小必须为 3。如果未指定值,则默认值是大小等于 3 的第一个数组维度。
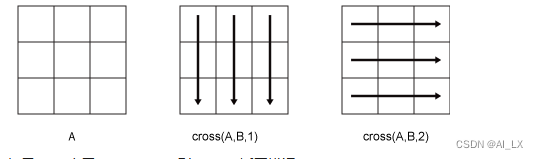
考虑两个二维输入数组:A 和 B:
cross(A,B,1) 将 A 和 B 的列视为向量,并返回对应列的叉积。
cross(A,B,2) 将 A 和 B 的行视为向量,并返回对应行的叉积。
如果 dim 大于 ndims(A),则 cross 返回错误。