参考：《漫画算法-小灰的算法之旅》

目录

1、排序算法的思想

2、具体步骤

3、插入排序的优化

4、时间复杂度和空间复杂度

5、代码

---

1、排序算法的思想

维护一个有序区，把元素一个个插入有序区的适当位置，直到所有元素都有序为止。

2、具体步骤

给定无序数组：

 把数组的首元素5作为有序区，此时有序区只有这一个元素：

 第一轮：让元素8和有序区的元素依次比较。8>5，所以元素8和元素5无需交换，此时有序区的元素增加到两个：

⭐注意，比较是从有序序列的末尾开始的，也就是想要插入的元素和有序区的最大者开始比起，如果比他大，直接插入在其后面，否则依次向前比较，直到找到该插入的位置。如果一个元素和插入元素相同，就把要插入的元素放在与其相等的元素后面。（——>插入排序是稳定的）

第二轮：

让元素6和有序区的元素依次比较。 6<8，所以把元素6和元素8进行交换；6>5，所以元素6和元素5无须交换。 此时有序区的元素增加到3个：

第三轮： 

让元素3和有序区的元素依次比较。 3<8，所以把元素3和元素8进行交换；3<6，所以把元素3和元素6进行交换；3<5，所以把元素3和元素5进行交换；此时有序区的元素增加到4个：

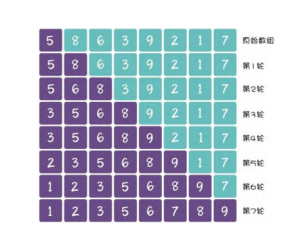
 依次类推，插入排序一共会进行（数组长度-1）轮，每一轮的结果如下：

3、插入排序的优化

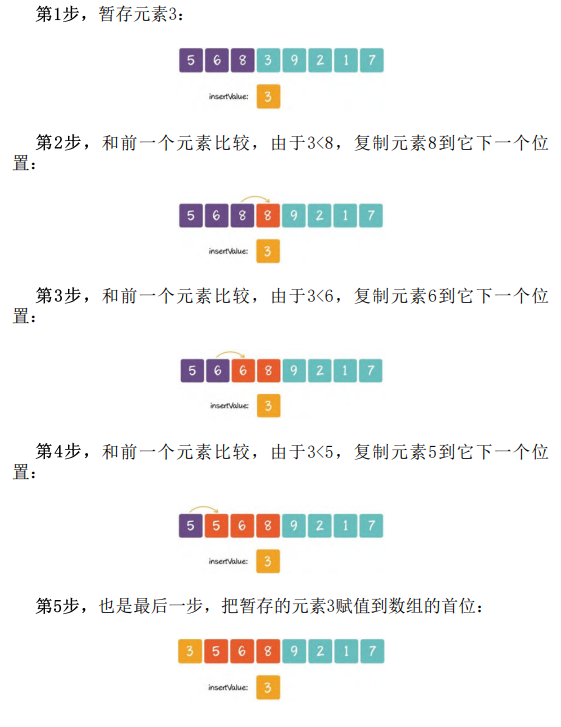
当我们把每一个新元素插到有序区的时候，并不需要老老实实进行元素的两两交换。

上面例子的第三轮中，我们需要让元素3逐个与有序区的元素进行比较和 交换，与8交换、与6交换、与5交换，最终交换到有序区的第一个位置。但是我们并不需要真的进行完整交换，只需把元素3暂存起来，再 把有序区的元素从前向后逐一复制。

4、时间复杂度和空间复杂度

插入排序要进行n-1轮，每一轮在最坏情况下的比较次数分别是1 次、2次、3次、4次……一直到n-1次，所以最坏时间复杂度是O(n^2)。

由于插入排序是原地排序，并没有借助额外的存 储空间，所以空间复杂度是O(1).

5、代码