目录

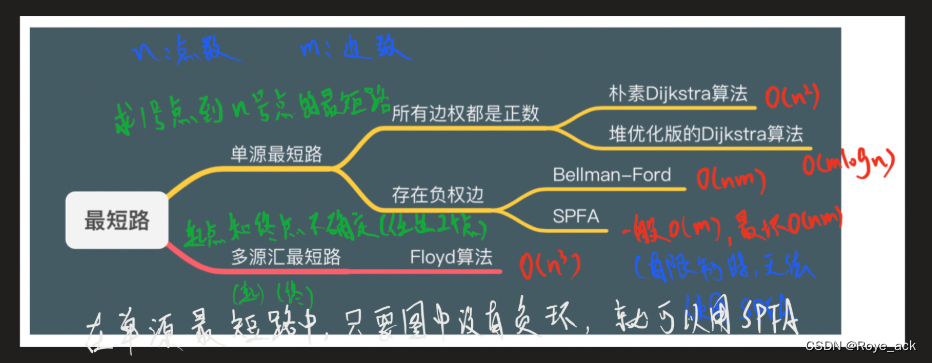
一、求1号点到n号点的最短路

1、所有边都是正数——Dijkstra

（1）朴素版dijkstra - 邻接矩阵

（2）堆优化版dijstra - 邻接表

2、存在负权边——spfa

3、dijkstra和spfa的区别

二、起点和终点未知，求某两点间最短路 —— Floyd

---

一、求1号点到n号点的最短路

1、所有边都是正数——Dijkstra

【蓝桥杯集训14】Dijkstra求最短路（3 / 3）_Roye_ack的博客-CSDN博客

（1）朴素版dijkstra - 邻接矩阵

初始化准备：

dist[i]=从1~i点最短距离   初始化dist[i]=0x3f3f3f3f   dist[1]=0

n次循环

{

        1、从1~n点中找到未标记的点中，离起点最近的点

        2、标记该点

        3、用该点更新到其他点的最小距离

}

    public static int dijkstra()
    {
        Arrays.fill(dist,0x3f3f3f3f);
        dist[1]=0;
        
        for(int i=0;i<n;i++) //n次循环
        {
            int t=-1;
            //先找出未标记的点中 距离起点最近的点
            for(int j=1;j<=n;j++)
                if(st[j]==0&&(t==-1||dist[j]<dist[t])) 
                    t=j;
            
            st[t]=1;
            
            //用t更新到其他点的最短距离
            for(int j=1;j<=n;j++) dist[j]=Math.min(dist[j],dist[t]+g[t][j]);
        }
        
        return dist[n];
    }

（2）堆优化版dijstra - 邻接表

初始化准备：

dist[i]=从1~i点最短距离   初始化dist[i]=0x3f3f3f3f   dist[1]=0

• 点1先入队，小顶堆q.offer({距离，点}） //按距离排序
• 小顶堆的作用就是优化在1~n中找离起点最近的点
• 标记该点
• 用该点更新到其他点的最小距离，没标记的入队

public static int dijkstra()
    {
        Arrays.fill(dist,0x3f3f3f3f);
        dist[1]=0;
        PriorityQueue<PII> q=new PriorityQueue<>();
        q.offer(new PII(0,1)); //按first排序 所以距离放前边
        
        while(!q.isEmpty())
        {
            var t=q.poll();
            int p=t.y;
            int d=t.x;
            
            if(st[p]==1) continue;
            st[p]=1;
            
            for(int i=h[p];i!=-1;i=ne[i])
            {
                int j=e[i];
                if(dist[j]>d+w[i]) 
                {
                    dist[j]=d+w[i];
                    q.offer(new PII(dist[j],j));
                }
            }
        }
        
        return dist[n];
    }

 

2、存在负权边——spfa

【蓝桥杯集训15】求最短路存在负权边——spaf算法（3 / 3）_Roye_ack的博客-CSDN博客

初始化准备：

dist[i]=从1~i点最短距离   初始化dist[i]=0x3f3f3f3f   dist[1]=0 

st[x]数组标记x节点是否在队列中

• 建立队列，队列初始只有节点1，标记节点1
• 取出队头节点x，取消该点标记，遍历x所有出边（x,y,z），若dist[y]>dist[x]+w，则更新最短路dist[y]=dist[x]+w，若y不在队列中，让y入队并标记
• 重复上述步骤，直到队列为空

求负环一般使用spfa算法，方法是用一个cnt数组记录每个点到源点的边数，一个点被更新一次就+1，一旦有点的边数达到了n那就证明存在了负环

    public static int spaf()
    {
        Arrays.fill(dist,0x3f3f3f3f);
        dist[1]=0;
        st[1]=1;
        Queue<Integer> q=new LinkedList<>();
        q.offer(1);
        
        while(!q.isEmpty())
        {
            var t=q.poll();
            st[t]=0;
            
            for(int i=h[t];i!=-1;i=ne[i])
            {
                int j=e[i];
                if(dist[j]>dist[t]+w[i])
                {
                    dist[j]=dist[t]+w[i];
                    if(st[j]==0) //如果当前队列里不存在该节点 则入队并标记
                    {
                        q.offer(j);
                        st[j]=1;
                    }
                }
            }
        }
        return dist[n];
    }

 

3、dijkstra和spfa的区别

• dijstra是局部最优的思想，也就是前面节点确定最短路后不会再更新，是拿已经最短的节点去更新它的后继节点，所以并不能及时更新每个节点的最小值

• spfa通过队列实现，出队就去掉标记，入队就打上标记，如果某点前驱节点更新，后继一定会跟着更新，也就是队列循环更新 直至队空，因此可以及时更新每个节点最小值

 

二、起点和终点未知，求某两点间最短路 —— Floyd

【蓝桥杯集训16】多源汇求最短路——Floyd算法（2 / 2）_Roye_ack的博客-CSDN博客

这个原理来自于动态规划，背板子就行 

public static void floyd()
    {
        for(int k=1;k<=n;k++)
            for(int i=1;i<=n;i++)
                for(int j=1;j<=n;j++)
                    d[i][j]=Math.min(d[i][j],d[i][k]+d[k][j]);
    }