前序:文章结构

1.一元导数
①一般函数求导
因为太简单的原因,事实上一般函数求导不会单独出现,大多数都是出现在各种特殊的求导过程中。只要掌握16个基本求导公式没问题。

②复合函数求导(主要链式法则)
这种一般是各种初等函数相互复合包含。
③隐函数求导
方法一:可以两边同时对x求导,然后表示为dy/dx=…的形式即可
方法二:可以利用多元函数中的公式如下。
方法三:一元微分形式不变性。



④反函数求导
即反函数的导数=原函数导数的倒数。
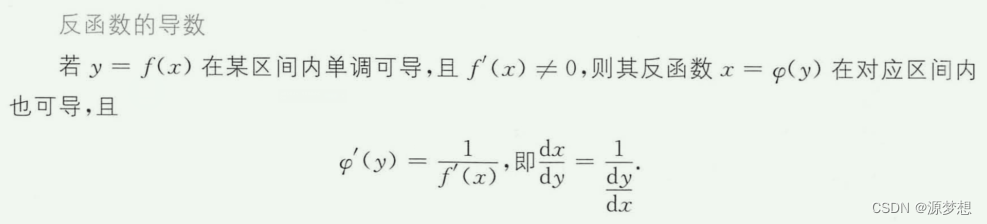
⑤参数方程求导
注意:二阶导的时候,要除以x对t求导。

⑥对数函数求导法
当含有根号,或者很”难受“的次幂时候,可以同时取对数简化求导过程。


⑦分段函数求导
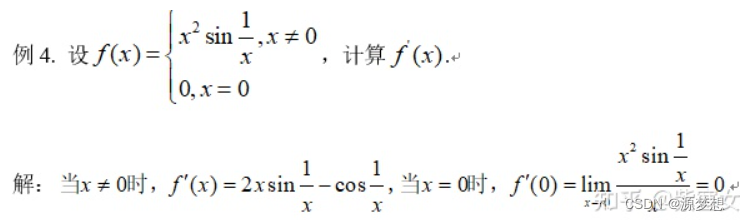
⑧高阶导数
正常求…
2.多元函数求导
①一般函数偏导数
本质就是一元函数导数。
②复合函数偏导数
本质就是一元函数复合导数。
③隐函数偏导数
1.有一个方程F(x,y,z)=0确定的
方法1:两边同时对x求导。
方法2:用公式偏z/偏x=-F’x/F’z
方法3:全微分形式不变性。
2.有一个方程组F(x,y,z,u,v)=0,G(x,y,z,u,v)=0确定的
两个方程两边同时对x求导,将偏u/偏x,偏v/偏x看作变量。利用克莱姆法则解方程组。
④高阶偏导数及混合偏导
注意高阶偏导虽然简单,单数特别容易出错。如下题:


⑤全微分
分别求x,y偏导带入即可。