🎇🎇🎇作者:
@小鱼不会骑车
🎆🎆🎆专栏:
《java练级之旅》
🎓🎓🎓个人简介:
一名专科大一在读的小比特,努力学习编程是我唯一的出路😎😎😎
今天小鱼讲到的是关于时间复杂度和空间复杂度的理解。



了解时间复杂度
- 时间复杂度
- 前言
- 时间复杂的讲解
- 如何简化时间复杂度
- 时间复杂度的计算
时间复杂度
前言
我们来举个例子!
假如我们有A,B两台电脑,A电脑的执行速度是1000次/s,B电脑的执行速度是1次/s,假如两台电脑都执行相同的代码,那么是不是我的A电脑会更快的完成任务。
答案是:对的!
但是我们改变一下条件,假设两台电脑需要完成一个查找数组中指定元素的任务,A电脑中的代码每次可以遍历1个元素,B电脑中的代码每次可以遍历100个元素。那么大家认为这两台电脑哪一个会更快的完成任务?
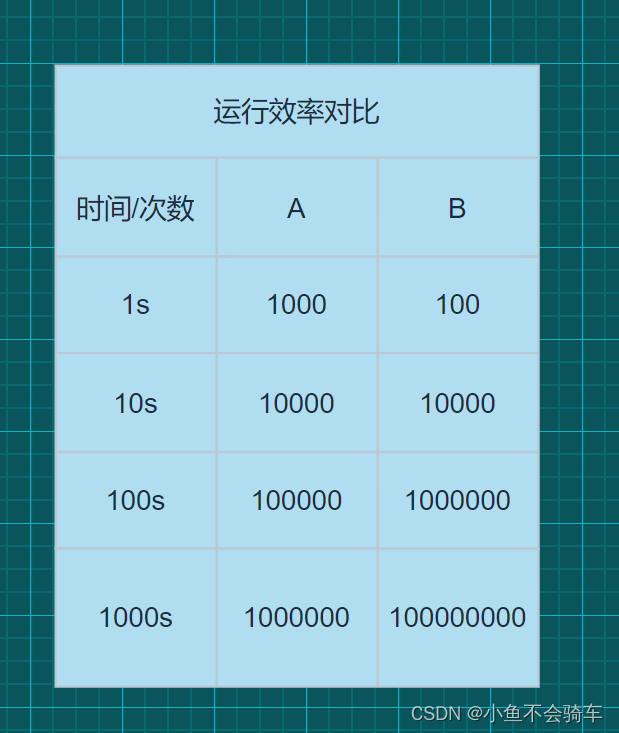
通过这个图表我们就可以看出,当运行到10秒时,我们的B对元素遍历的次数已经和A持平了,再往后面我们的B的遍历次数更是远超A.
于是我们可以通过上图的对比看出,哪怕是电脑的性能很好很优良,但是却还依然跑不过B,这就体现到了代码运行效率的重要性!
时间复杂的讲解
上面举得例子只是为了让大家知道代码运行效率的重要性,下面才是真正的讲解如何计算代码的运行效率!
大家看这段代码!
public static void main(String[] args) {
int n=100;
while ((n)!=0) {
n--;
}
}
大家认为这段代码会运行多久?
可能就会有同学回答说:这个要放计算机上跑跑才知道吧…
那我如果将n改为10000呢?需要运行多久啊?
同学:这个…要不再测试一次?
其实呀,我们并不能精准的测量出程序运行的时间,有的计算机的运行速度会快一些,有的则会慢一些…于是呢,就有人提出了用计算机的语句的执行次数来当作计算机的时间效率,而不是运行的时间。
我们来算算上述的代码执行了多少次
为了方便讨论,这里我们把每一条语句的执行时间都看做是一样的,记为一个时间单元

由于黄色的最后还需要判断一次,所以需要n+1个时间单元 !
那么我们就可以计算出这个程序的语句执行了多少次,我们可以用函数来表达:y=n+n+1+1,化简就是:y=2n+2;函数图像就是
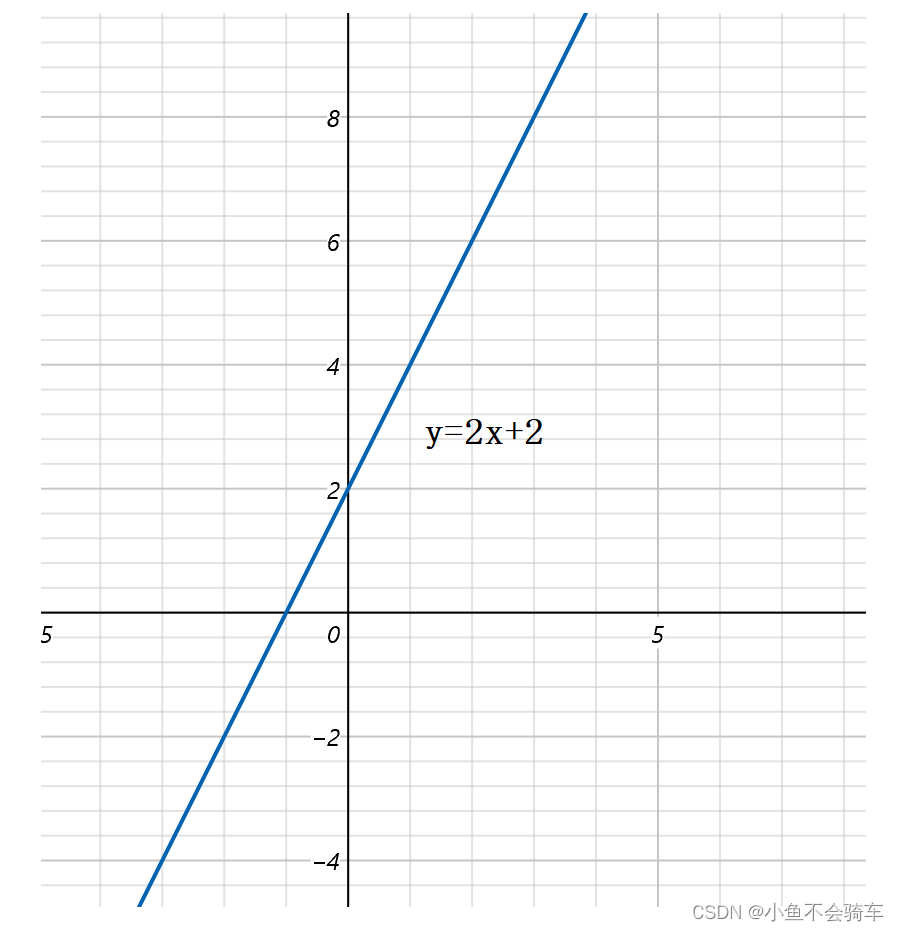
所以,如果要预测程序运行的时间我们可以把运行时间函数求出来。
可是如果光看这个函数还是有些复杂啊!
其实呀,我们平时都会对这些函数进行简化的,使得它既简单又没有失去函数得主要特性。
咦?那怎么简化啊?
如何简化时间复杂度
对于时间复杂度来说,我们比较关心的就是影响最终结果的最高次项。
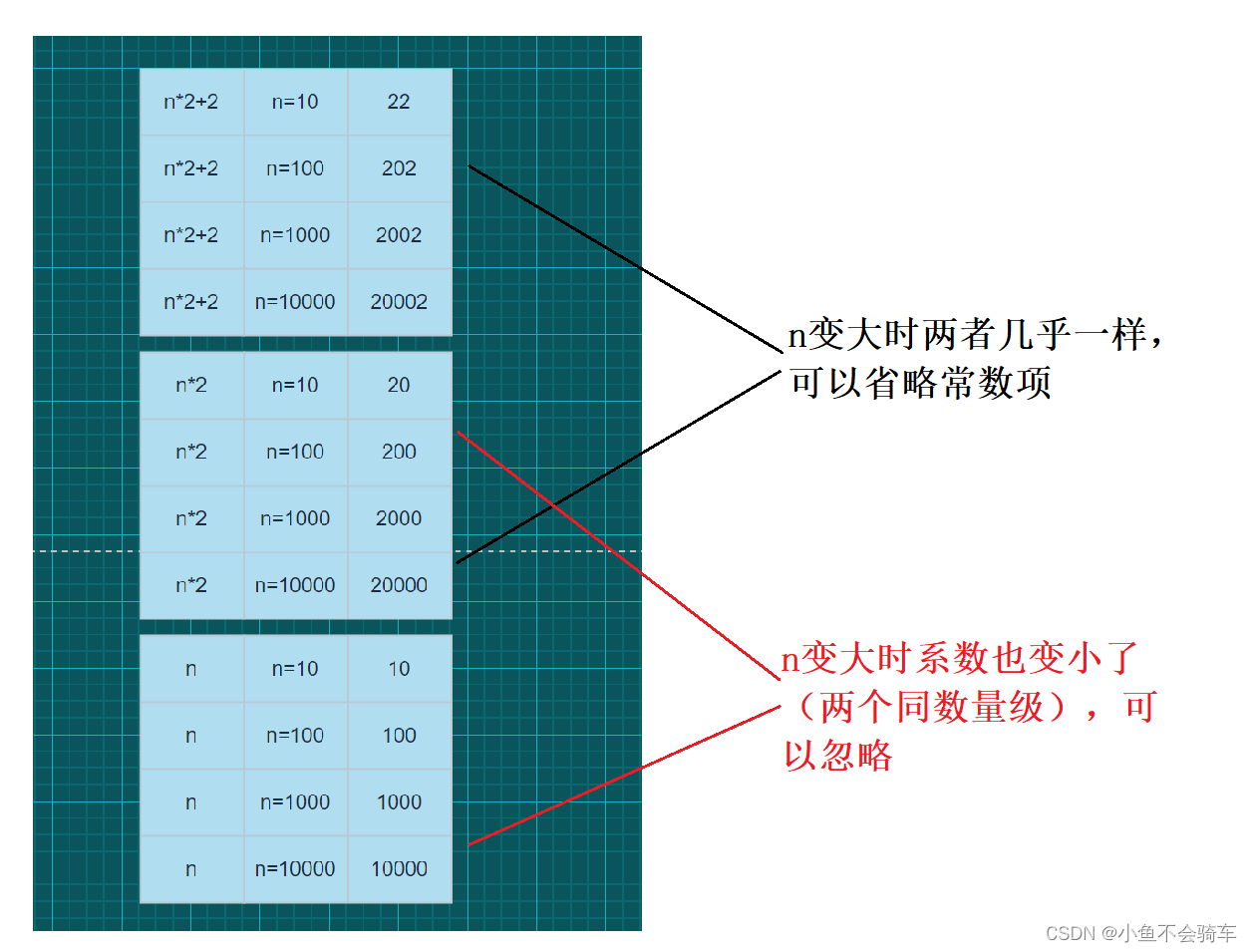
比如说:T(n)=2n+2, 当n非常大的时候常数2和n的系数2对函数结果的影响就很小了
例如:
T(n)=n+1 忽略常数项 T(n)~n
T(n)=n+n^2 忽略低阶项 T(n)~n^2
T(n)=3n 忽略最高阶的系数 T(n)~n
所谓低阶项就是当n很大时,该项对于这个数的影响很小,比如n相对于n^2来说,n就是低阶项!
对此呢,我们有一个比较的关系,不同项进行比较只保留最高阶项,比较关系如下
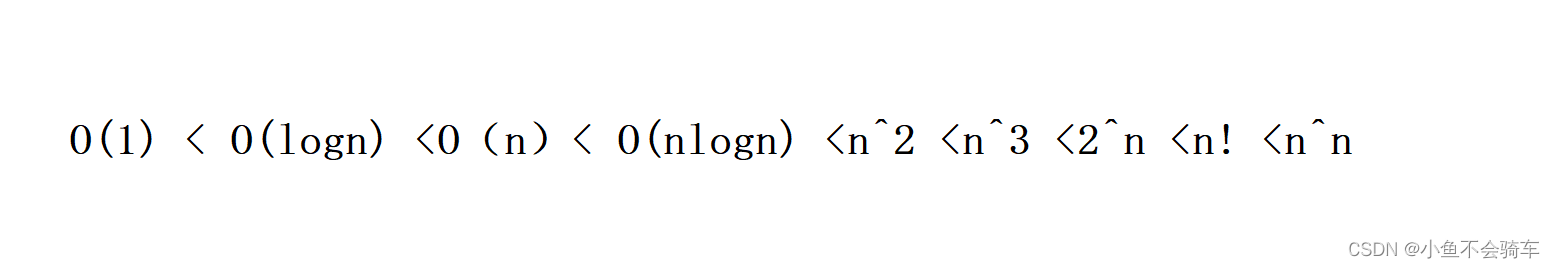
化简后的函数可以代表原函数的总体趋势,并且简化后的式子就可以称为这个算法的时间复杂度,记作O(f(n)),其中f(n)是简化后的式子,例如刚才的T(n)=2*n+2,简化后为T(n)~ f(n) ~ n,所以我们也可以记作O(n).
更准确地说O代表了运行时间函数的一个渐进上界,即T(n)在数量级上小于等于f(n)
那我们如何计算时间复杂度呢?
时间复杂度的计算
经过了前面的两个小部分的讲解,我们也可以总结出:计算算法复杂度大O的方法
一.得出运行时间的函数
二.对该函数进行简化
1.用常数1取代运行时间中所有加法常数
2.修改后的函数只保留最高阶项
3.如果最高阶项存在,并且不是1,则忽略这个最高项数的系数
举个例子,看下面代码:

我们可以看出,T(n)=5,我们可以对这个函数进行简化,将他的常数项用1来取代,又因为该函数没有最高阶项,所以他的时间复杂度就是O(1)。
O(1)也被称为常数阶
当然啦,如果我们一个一个去数语句再去计算函数是很麻烦的,有没有简便一些的方法吗?
其实是可以偷偷懒的,一般来说程序最内层执行次数最多的语句就决定了整个函数的趋势。
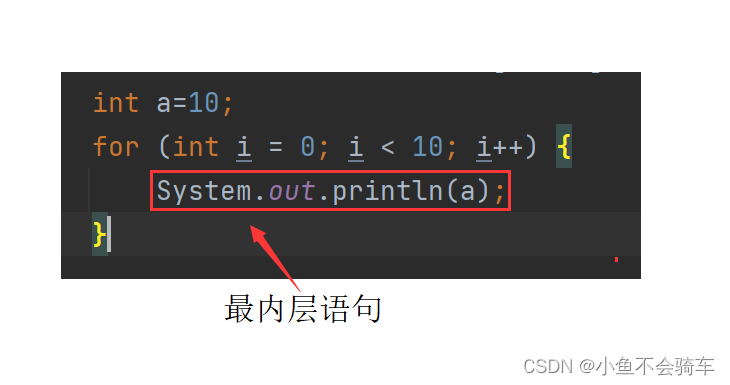
我们只需要找到最内层语句执行次数的规律就行!所以我们就可以清楚的得出上面的时间复杂度是O(n).
并且呢,我们也可以根据这个方法得出下面这个代码的时间复杂度O(n^2)
.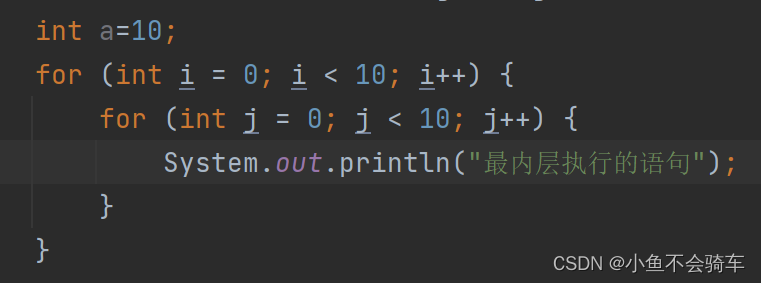
如果还有人不太理解这个O(n^2)这个时间复杂度的意思,我给大家用数学的角度来算一下!
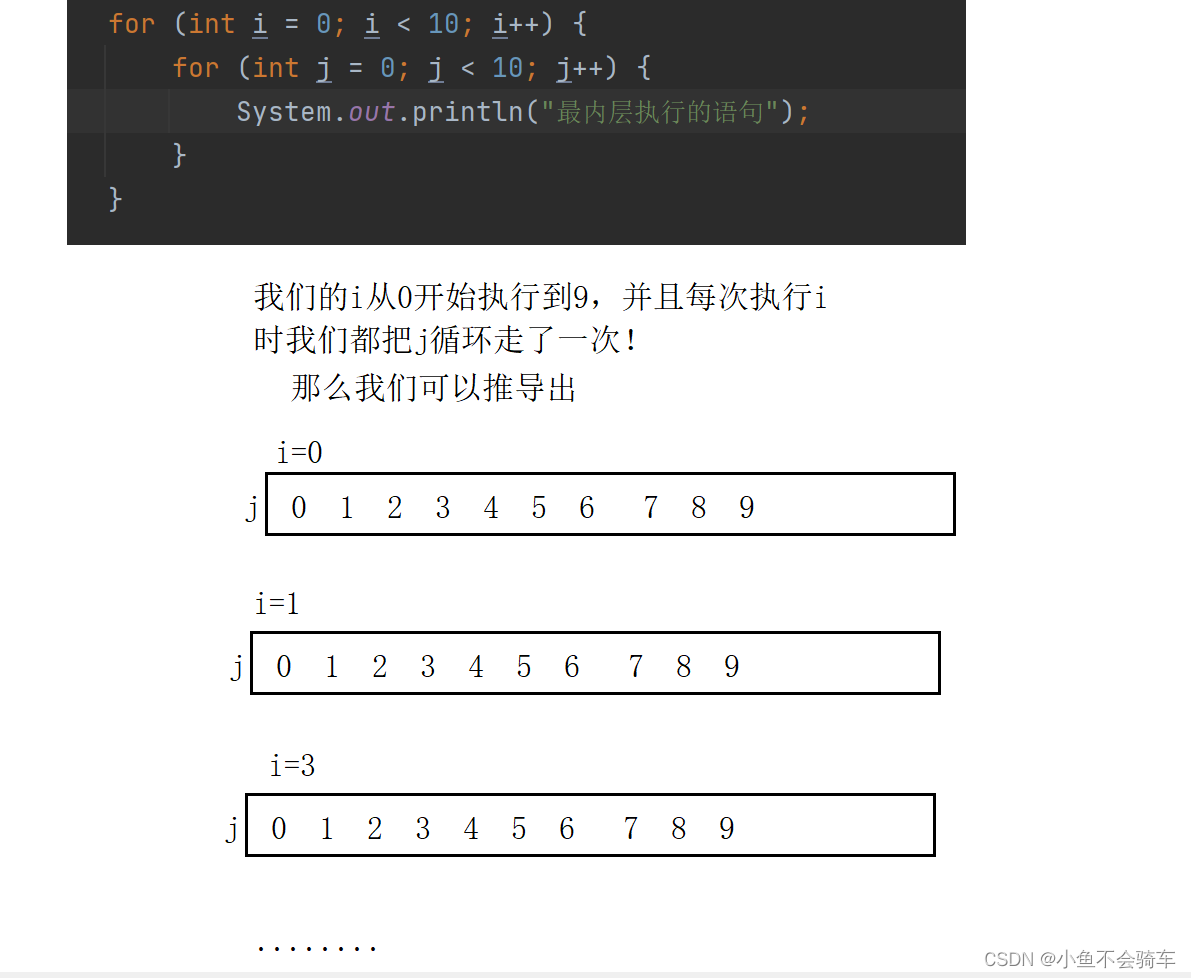

所以我们可以理解为上述的代码的时间复杂度为O(n^2)
下面再来介绍最后一个比较牛 * 的时间复杂度O(log2N),读作log以2为底N的对数。
怎么个牛 * 法呢?二分查找大家都知道吧,在一个有序数组里查找指定的元素,如果我们用从前往后遍历的方式来查找,我们用这个世界的人口举例
我们简单认为是76亿人,所以我们假设这个数组是76亿个元素,如果我们想从这76亿个元素中查找到一个指定的元素,那么最坏的情况就是查找76亿次,多么庞大的次数啊。
但是!假设这是一个有序数组,该数组有76亿个元素,大家猜猜我们需要查找多少次?
答案是我们只需要查找33次,就可以找到这个要被查找的元素,牛不牛!
我们再来看看O(logN)的函数图像
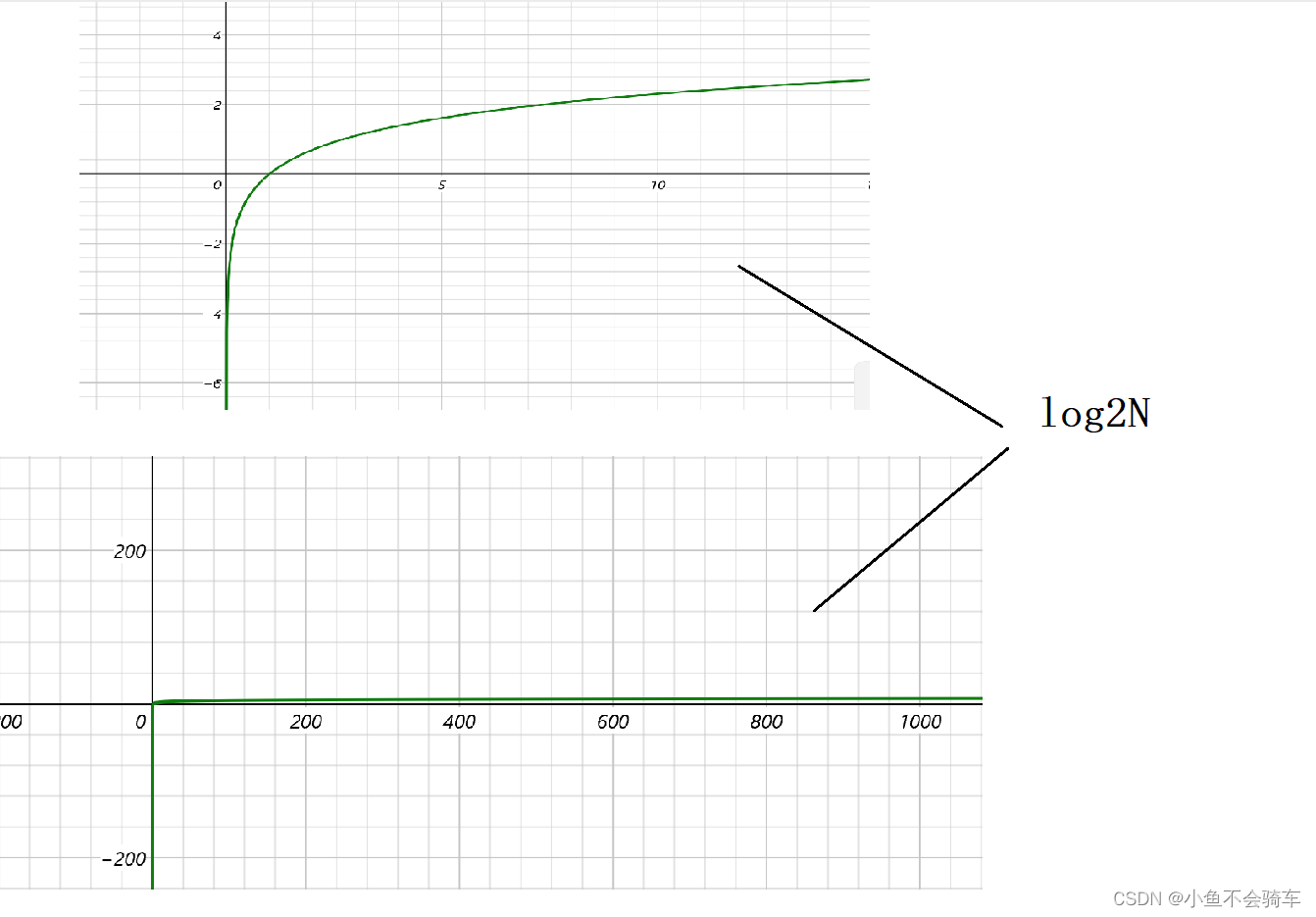
上下图对比,它随着自变量的增大,因变量增长的很慢很慢!
int a=1;
while (a<=n) {
a*=2;
}
这段代码的复杂度就是对数级别的,O(logn)。
怎么计算它的时间复杂度呢?

复杂度的内容好多,会一直伴随着我们学习数据结构与算法,所以我们现在只需呀简单理解复杂的的含义就行!