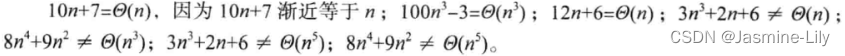渐近记法

3.1 引言

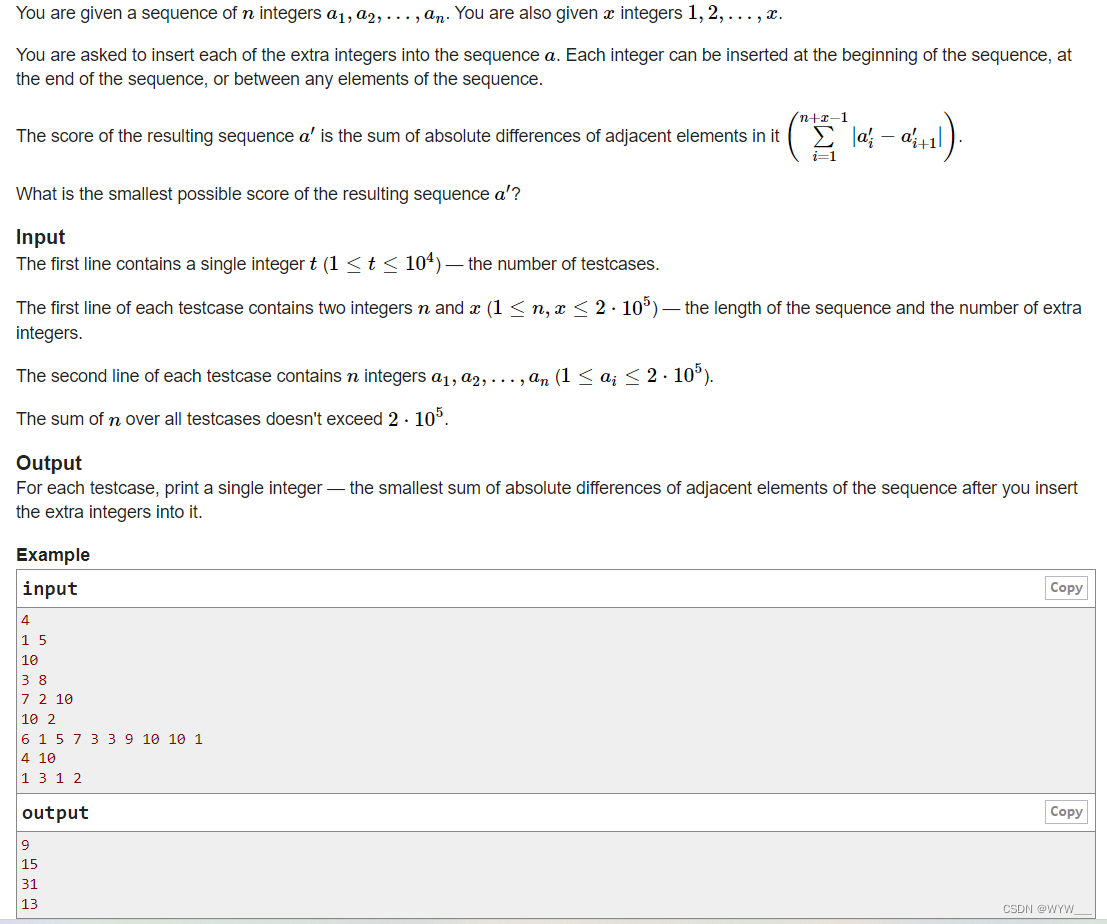
考察程序的操作计数和执行步数有两个重要的原因：

• 1)预测程序运行时间如何随着实例特征的变化而变化；

• 2)对两个功能相同的程序，比较它们的时间复杂度。

存在问题：

• 在使用操作计数时，我们关注的是某些“关键”的操作，而忽略了其他的操作。
• 步数的概念是不精确的。

渐近分析方法主要确定的是复杂函数中的最大项(但不包括最大项的系数)。

3.2 渐近记法

3.2.1 大0记法

定义3-1 令p(n)和g(n)是两个非负函数。称p(n)渐近地大于q(n) (p(n)渐近地优于q(n))，当且仅当：
$$\underset{n\to \infty }{\lim }\frac{q(n)}{p(n)}=0$$
称q(n)渐近地小于p(n)，当且仅当p(n)渐近地大于q(n)。称p(n)渐近地等于q(n)，当且仅当任何一个都不是渐近地大于另一个。

常见时间复杂度项

f(n)作为实例特征n的函数，表示一个程序的时间或空间复杂度。因为程序的时间或空间复杂度是一个非负数，所以我们假设函数f对所有n都是非负值。

图3-3给出了经常在步数分析中出现的项。虽然其中所有项的系数都是1，但是在实际分析中，这些项的系数都有不同的值。图3-3的对数都没有对数基，原因是对于任何大于1的常数a和b，都有：
$$lo{g}_{a}n=lo{g}_{b}n/lo{g}_{b}a,因此lo{g}_{a}n和lo{g}_{b}n是渐近相等的。$$
利用定义3-1，对图3-3的所有项，可以排列出它们的大小顺序如下(其中<表示渐近地小于)：
$$1<logn<n<nlogn<n^2<n^3<2^n<n!$$

**渐近记法(asymptotic notation)**描述的是大实例特征的时间或空间复杂度。我们将用它来分析步数(其实还可以用它来分析空间复杂度和操作步数)。时间复杂度和步数是同义词。如果实例特征只含有一个变量，例如n，渐近记法就用步数中渐近最大的一项来描述复杂度。
表示法f(n)=0(g(n))(读作"f(n)is big of g(n)")代表f(n)渐近小于或等于g(n)。在渐近的意义上，g(n)是f(n)的上限。

在渐近复杂度分析中，我们要确定一个最大项以表示复杂度，而且把这个最大项的系数置为1。

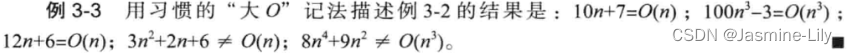
**【注意】**f(n)=O(g(n))与O(g(n))=f(n)不同。实际上，后者没有意义。符号“=”通常表示相等关系，此处表示的意思为“是”。因此，要把符号“=”读作“是”，而不是“等于”。

3.2.2 渐近记法Ω

记法f(n)=Ω(g(n))(读作“f(n)is Ω of g(n)”)表示f(n)渐近大于或等于g(n)。因此，在渐近意义上，g(n)是f(n)的下界。

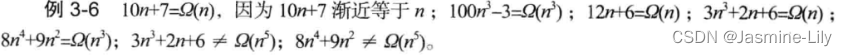
3.2.3 渐近记法Θ

记法f(n)= Θ(g(n))(读作“f(n)is Θ of g(n)”)表示f(n)渐近等于g(n)。