原文:https://mp.weixin.qq.com/s/Uuri-FqRWk3V5CH7XrjArg
1 灰色关联分析法简介
白色系统是指信息完全明确的系统,黑色系统是指信息不完全明确的系统,而灰色系统是介于白色与黑色系统之间的系统,是指系统内部信息和特征是部分已知部分未知。
灰色系统理论提出了灰色关联分析的概念,其目的是寻找各因素之间数值的关系。
灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断不同序列之间是否具有紧密的联系, 其基本思路是通过线性插值的方法将系统因素的离散行为观测值转化为分段连续的折线,进而根据折线的几何特征构造测度关联程度的模型。
折线的几何形状越接近, 则相应序列之间的关联度就越大,反之就越小。 灰色关联分析实际上是动态指标的量化分析,充分体现了动态意义。
灰色关联度(Grey Relational Analysis, GRA)是指两个系统或两个因素之间关联性大小的量度, 根据其大小我们可以分清因素对系统发展影响的主次关系。
注意:之所以称为关联,是因为他只反映哪一个指标和要对比的指标最有关系,而不反映相关性。他和相关性系数无关,也不对等。最后得出来的系数,也只是做一个排序。
灰色关联分析法特点:
- 不需要应变量,参考变量服从正态分布,对样本数据没有要求,适合小样本数据。
- 能够将自变量和参考变量的关联性大小排序,从而得到重要性排序的评价,本身的关联度没有实际意义,比如得出关联度为0.95,这个数字只用排序,并不能像相关性0.95一样得出他们高度正相关。
- 缺点在于只能排序,不能得出确切的相关性,不属于相关性分析范畴,只归入综合评价方法里。
2 灰色关联分析法计算
1)确定指标
2)得到统计数据列成矩阵R
假设选取了 X 个指标,每个指标有 Y 个年份的统计数据。
为了便于计算,将 X 个指标的 Y 个年份的统计数据列成矩阵 R,则有:

3)对矩阵 R 进行无量纲化处理
灰色关联度的计算方法有很多,如绝对关联度、斜率关联度、速率关联度、 B 型关联度、面积关联度等等,这里选择最大最小归一化。

4)确定参考列和对比列
记消除量纲的一个对比序列为 x 0 ( t ) x_0(t) x0(t),参考序列为 x 1 ( t ) x_1(t) x1(t),则两个序列同在一个时刻 k k k 的值分别为 x 0 ( k ) , x 1 ( k ) x_0(k),x_1(k) x0(k),x1(k) 即:

x 0 ( k ) , x 1 ( k ) x_0(k),x_1(k) x0(k),x1(k)的绝对差值:

5)确定绝对差值的最小值和最大值

6)计算关联系数
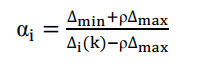
Δ i ( k ) \Delta_i(k) Δi(k) 为 k k k 时刻两比较序列的绝对差,在灰色理论中 ρ ∈ ( 0 , 1 ) \rho\in(0,1) ρ∈(0,1) ,通常研究学者都是取 0.5。
如果 x 0 ( k ) x_0(k) x0(k)是最优值数据列, α i \alpha_i αi 越大,越好;如果 x 0 ( k ) x_0(k) x0(k)是最劣值数据列, α i \alpha_i αi 越小,越不好。
7)计算目标层关联度

式中的 W W W 可以通过AHP方法计算,也可以对 α \alpha α 直接取均值。
8)确定评价等级

3 python 实现
现在有这样一组数据,通过对某健将级女子铅球运动员的跟踪调查,获得其 1982 年至 1986 年每年最好成绩及16 项专项素质和身体素质的时间序列资料,见表,试对此铅球运动员的专项成绩进行因素分析。

# 参考:https://blog.csdn.net/PY_smallH/article/details/121491094
# 最下面写了三个函数分别为gain,cost,level_,用于无量纲化,被GRA调用
def GRA(df,normaliza="initial",level=None,r=0.5):
'''
df : 二维数据,这里用dataframe,每一行是一个评价指标,要对比的参考指标放在第一行
normaliza :["initial","mean"] 归一化方法,默认为初值,提供初值化或者均值化,其他方法自行编写
level :为None默认增益型,
可取增益型"gain"(越大越好),成本型"cost"(越小越好),
或者dataframe中的某一列,如level="level","level"是列名,这列中用数字1和0表示增益和成本型
r : [0-1] 分辨系数
越大,分辨率越大; 越小,分辨率越小,一般取0.5
'''
# 判断类型
if not isinstance(df,pd.DataFrame):
df = pd.DataFrame(df)
# 判断参数输入
if (normaliza not in ["initial","mean"]) or (r<0 or r>1):
raise KeyError("参数输入类型错误")
# 增益型的无量纲化方法
if level == "gain" or level == None:
df_ = gain(df,normaliza)
#成本性无量纲化方法
elif level == "cost":
df_ = cost(df,normaliza)
else:# 有增益有成本性的无量纲化方法
try:
df.columns.get_loc(level) # 尝试获得这一列的列索引,判断输入的列名有没有,返回这个列的索引下标
except:
raise KeyError("表中没有这一列")
df_ = level_(df,normaliza,level)
df_.drop(level,axis=1,inplace=True)# 加的level这一列对总体没用,最后把这一列删除再做关联分析
df_ = np.abs(df_ - df_.iloc[0,:]) # 每一行指标和要参考的指标做减法,取绝对值。
global_max = df_.max().max()
global_min = df_.min().min()
df_r = (global_min + r*global_max)/(df_ + r*global_max) # 求关联矩阵
return df_r.mean(axis=1)
# gain增益型
def gain(df,normaliza):
for i in range(df.shape[0]):
if normaliza == "initial" or normaliza==None:
df.iloc[i] = df.iloc[i]/df.iloc[i,0]
elif normaliza == "mean":
df.iloc[i] = df.iloc[i]/df.mean(axis=1)
return df
# cost成本型
def cost(df,normaliza):
for i in range(df.shape[0]):
if normaliza == "initial" or normaliza==None:
df.iloc[i] = df.iloc[i,0]/df.iloc[i]
elif normaliza == "mean":
df.iloc[i] = df.mean(axis=1)/df.iloc[i]
return df
# 数据如下
x = np.array([
[13.6,14.01,14.54,15.64,15.69],
[11.50,13.00,15.15,15.30,15.02],
[13.76,16.36,16.90,16.56,17.30],
[12.41,12.70,13.96,14.04,13.46],
[2.48,2.49,2.56,2.64,2.59],
[85,85,90,100,105],
[55,65,75,80,80],
[65,70,75,85,90],
[12.80,15.30,16.24,16.40,17.05],
[15.30,18.40,18.75,17.95,19.30],
[12.71,14.50,14.66,15.88,15.70],
[14.78,15.54,16.03,16.87,17.82],
[7.64,7.56,7.76,7.54,7.70],
[120,125,130,140,140],
[80,85,90,90,95],
[4.2,4.25,4.1,4.06,3.99],
[13.1,13.42,12.85,12.72,12.56]
])
df1 = pd.DataFrame(x)
可得到最终的关联系数:
0 1.000000
1 0.588106
2 0.662749
3 0.853618
4 0.776254
5 0.854873
6 0.502235
7 0.659223
8 0.582007
9 0.683125
10 0.695782
11 0.895453
12 0.704684
13 0.933405
14 0.846704
15 0.745373
16 0.726079
第一行是铅球专项成绩x0,本身和自己最关联,这个不用看,剩下关联最强的就是x13全蹲,这样可以做针对性训练。最后还可以排个序。
再讨论一下这个关联系数矩阵,步骤中第五步求出的。针对上面的,关联矩阵如下:

画一个图,从里面挑几行出来画,要不太多了,看不清楚。

挑的数据为[0,1,2,3,4,13,16]这几行,其中0就是参考的指标。
可以看得出来,x13是关系最强的,所以和0的那条直线挨的最近,1,2,3中3是最强的,所以红色的线也在上面。
这就是一开始说的,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。
参考:
基于AHP-灰色关联分析法的沈阳市沈河区住区景观综合评价研究-王文文.
https://blog.csdn.net/PY_smallH/article/details/121491094