第九章哈希表 AcWing 2 1549. 集合相似度

原题链接

AcWing 1549. 集合相似度

算法标签

哈希表位运算

思路

使用unordered_set数据结构将数据插入指定集合

如何计算Nc（两集合交集）

在这里插入图片描述

如何计算Nt（两集合并集）

在这里插入图片描述

输出问题

WA 精度丢失

printf("%.1lf%%\n", 100.*nc/nt);

printf("%.1lf%%\n", (double)nc / nt * 100);

显然 100.*nc产生了精度丢失，但是，对于浮点数运算，
无法保证精度丢失会在哪次运算产生，
甚至无法保证之前未产生精度丢失的数据再进行相同计算，是否会导致精度丢失
精度丢失往往会导致计算结果不准确，
解决方案
比较保险的方案是对于计算结果增加一个精度值（精度值的选择依题意，一般取1e-8）,但是Acwing此题测试数据较强，加一个精度值依旧Wrong Answe，PAT数据较弱，无论是否增加一个精度值，都可以AC。
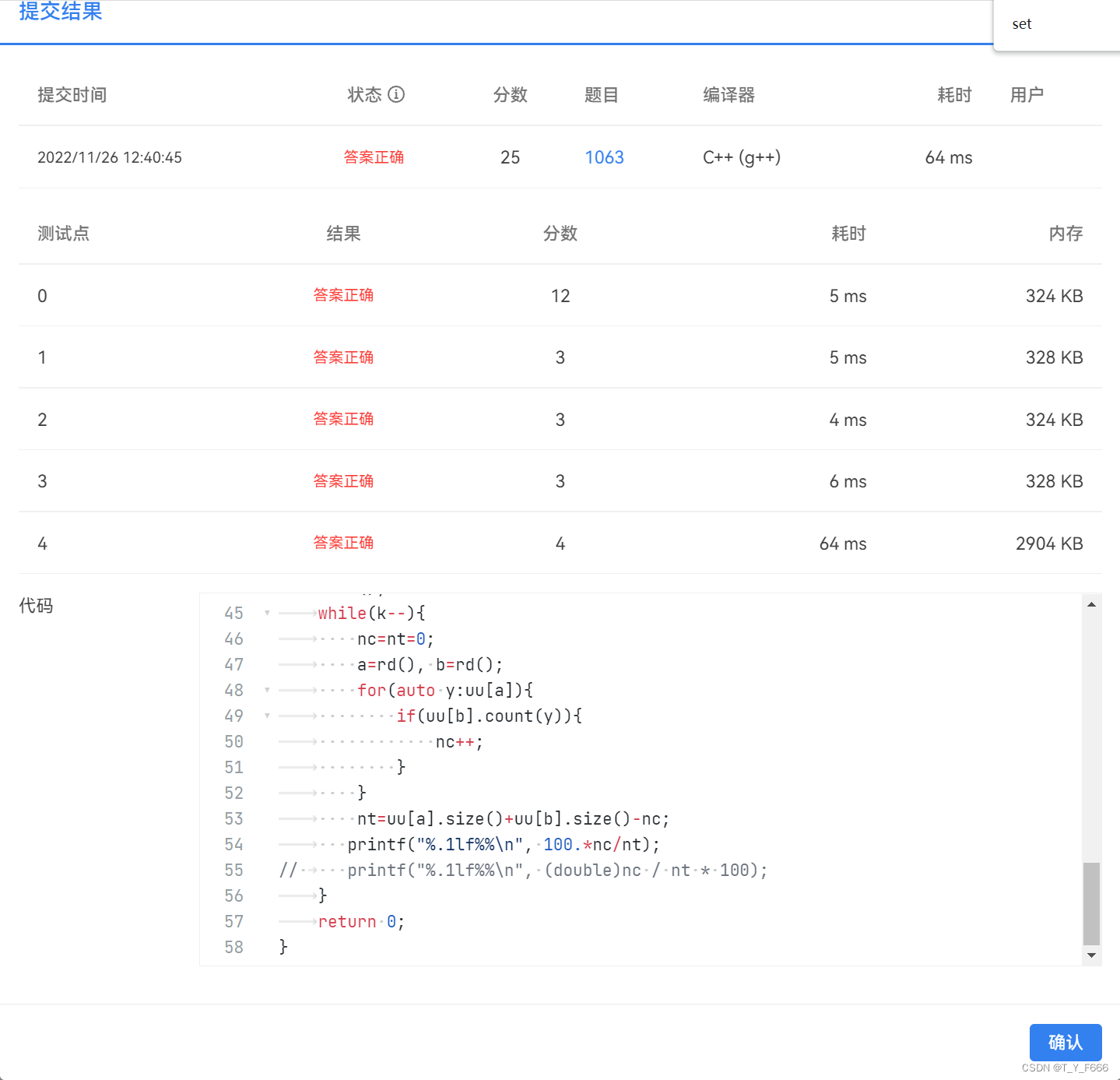
在这里插入图片描述
更为保险的方案是对于计算结果先进行精度转换，再进行精度计算
AC

// (double)nc 进行精度转换
// / nt * 100 精度计算 
printf("%.1lf%%\n", (double)nc / nt * 100);

// nc*1.0 对于整数*1.0 相当于只进行精度转换 未进行精度计算 
// /(nt)* 100 进行精度计算 
printf("%.1lf%%\n",(nc*1.0)/(nt)* 100);

代码

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define int long long
#define xx first
#define yy second
#define ump unordered_map
#define us unordered_set
#define pq priority_queue
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
typedef pair<int, int> PII;
const int N=55, INF=0x3f3f3f3f3f3f3f3f, MOD=1e9+7;
const double Exp=1e-8;
//int t, n, m, cnt, ans;
int n, m, x, a, b, nc, nt, k;
double res;
us<int> uu[N];
inline int rd(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
void put(int x) {
    if(x<0) putchar('-'),x=-x;
    if(x>=10) put(x/10);
    putchar(x%10^48);
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	n=rd();
	rep(i, 1, n+1){
	    m=rd();
	    while(m--){
	        x=rd();
	        uu[i].insert(x);
	    }
	}
	k=rd();
	while(k--){
	    nc=nt=0;
	    a=rd(), b=rd();
	    for(auto y:uu[a]){
	        if(uu[b].count(y)){
	            nc++;
	        }
	    }
	    nt=uu[a].size()+uu[b].size()-nc;
	   // printf("%.1lf%%\n", 100.*nc/nt);
	   printf("%.1lf%%\n", (double)nc / nt * 100);
	}
	return 0;
}