目录
一.LDA的应用方向
二.朴素贝叶斯的分析
三.Gamma函数
四.Beta分布
五.Beta分布的期望
六.LDA涉及的主要问题
1.共轭先验分布
①.二项分布的最大似然估计
②.二项分布与先验举例
③.上述过程的理论解释
④.先验概率和后验概率的关系
⑤.伪计数
⑥.共轭先验的直接推广
2.Dirichlet分布
①.Dirichlet分布的期望
②.Dirichlet分布分析
③.对称Dirichlet分布
④.对称Dirichlet分布的参数分析
⑤.参数α对Dirichlet分布的影响
3.LDA模型
①.LDA的解释
②.详细解释
③.参数的学习
④.似然概率
4.Gibbs采样算法学习参数
①.联合分布
②.计算因子
③.词分布和主题分布
七.代码实现
八.三个矩阵和三个向量
九.数据处理流程
十.超参数的确定
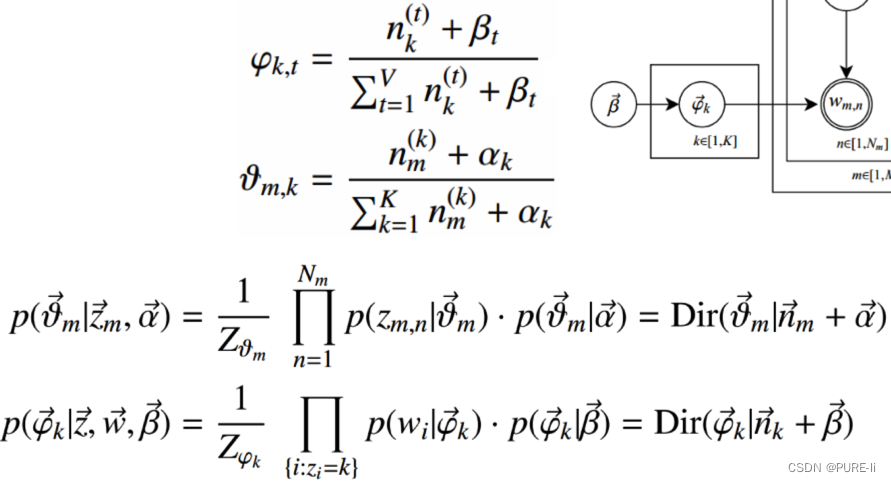
十一.一种迭代求超参数的方法
十二.主题个数的确定
十三.概率分布的困惑度/复杂度Perplexity
十四.困惑度Perplexity与主题模型
十五.PageRank
十六.TextRank
十七.LDA总结
一.LDA的应用方向
1.信息提取和搜索
语义分析
2.文档分类/聚类、文章摘要、社区挖掘
3.基于内容的图像聚类、目标识别
以及其他计算机视觉应用
4.生物信息数据的应用
二.朴素贝叶斯的分析
1.可以胜任许多文本分类问题。
2.无法解决语料中一词多义和多词一义的问题——它更像是词法分析,而非语义分析。
3.如果使用词向量作为文档的特征,一词多义和多词一义会造成计算文档间相似度的不准确性。
4.可以通过增加“主题”的方式,一定程度的解决上述问题:
一个词可能被映射到多个主题中
——一词多义
多个词可能被映射到某个主题的概率很高
——多词一义
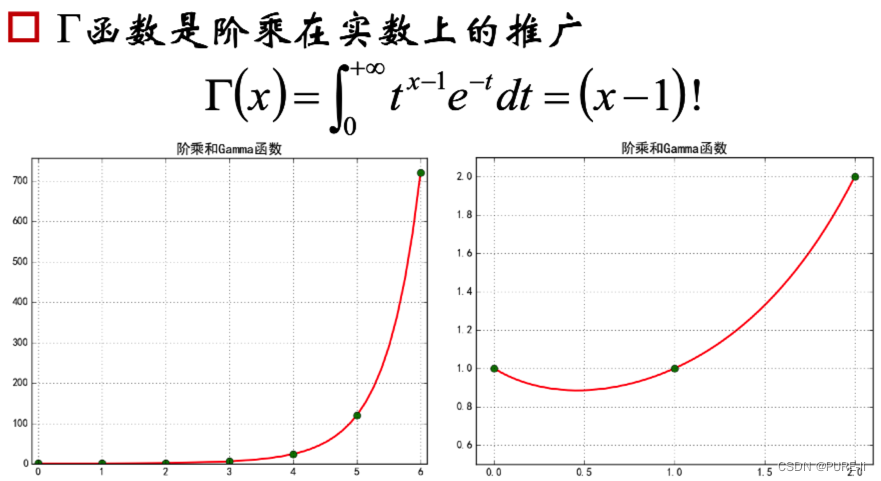
三.Gamma函数
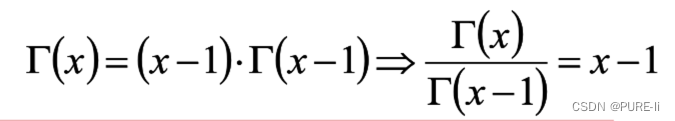
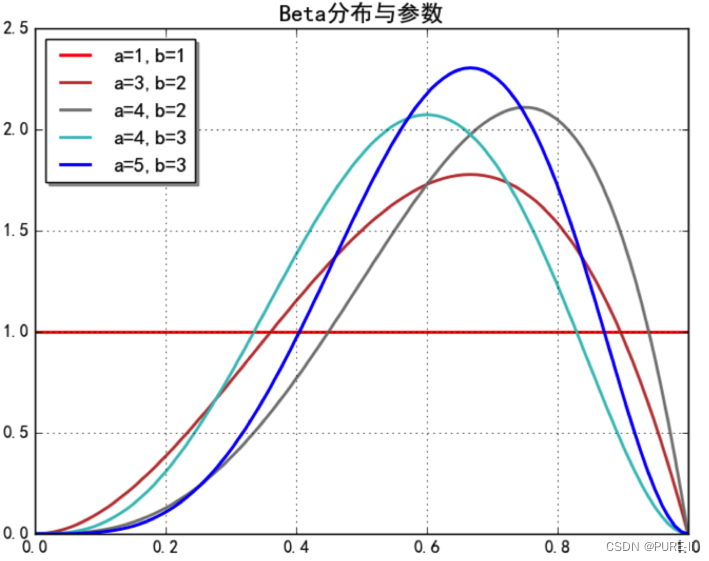
四.Beta分布

五.Beta分布的期望
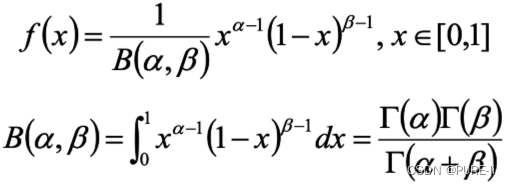
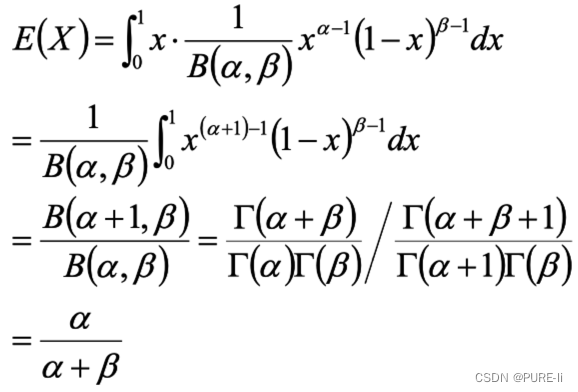
六.LDA涉及的主要问题
1.共轭先验分布
由于x为给定样本,P(x)有时被称为“证据”,仅仅是归一化因子,如果不关心P(θ|x)的具体值,只考察θ取何值时后验概率P(θ|x)最大,则可将分母省去。
![]()
在贝叶斯概率理论中,如果后验概率P(θ|x)和先验概率p(θ)满足同样的分布律,那么,先验分布和后验分布被叫做共轭分布,同时,先验分布叫做似然函数的共轭先验分布。
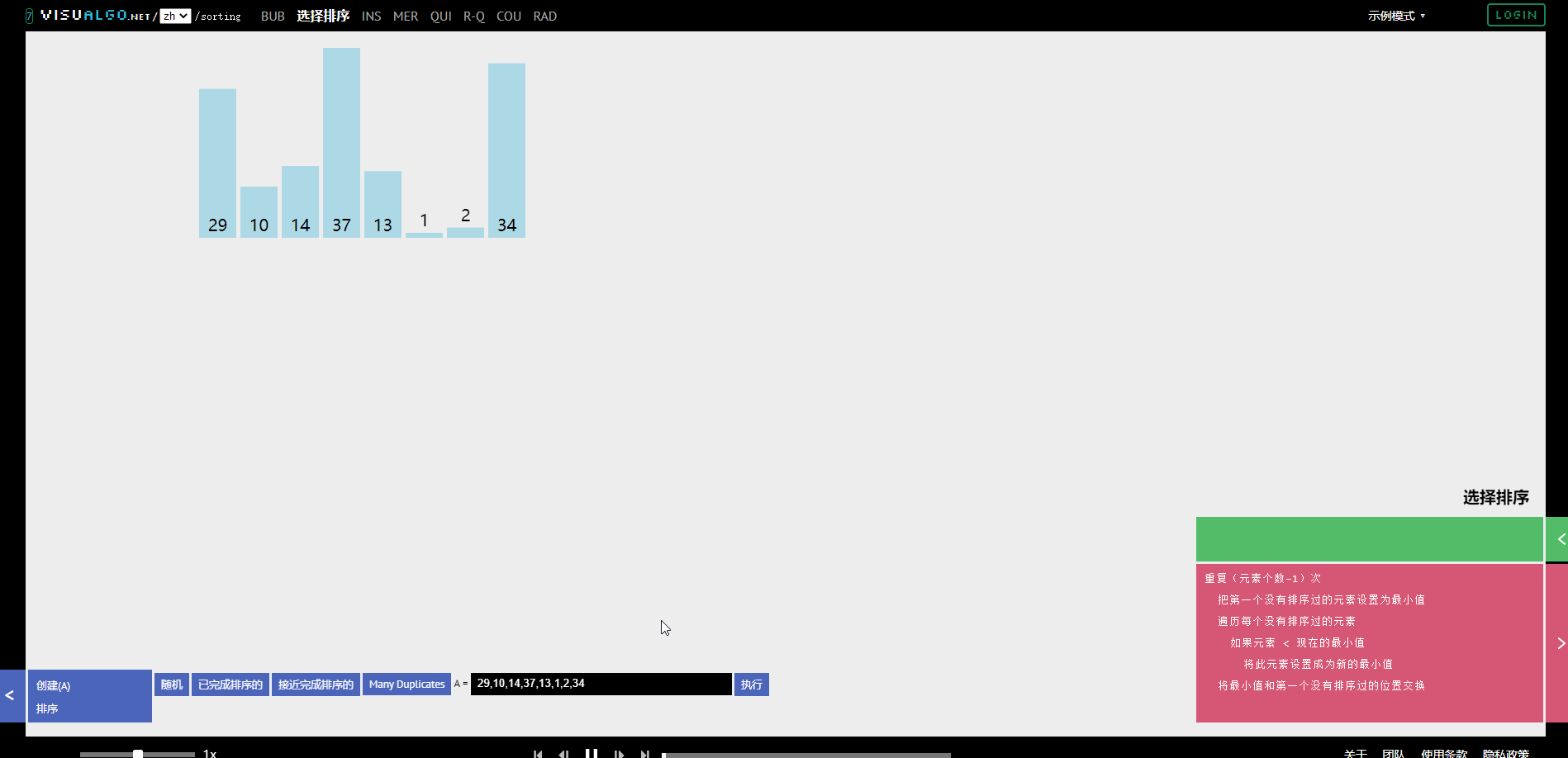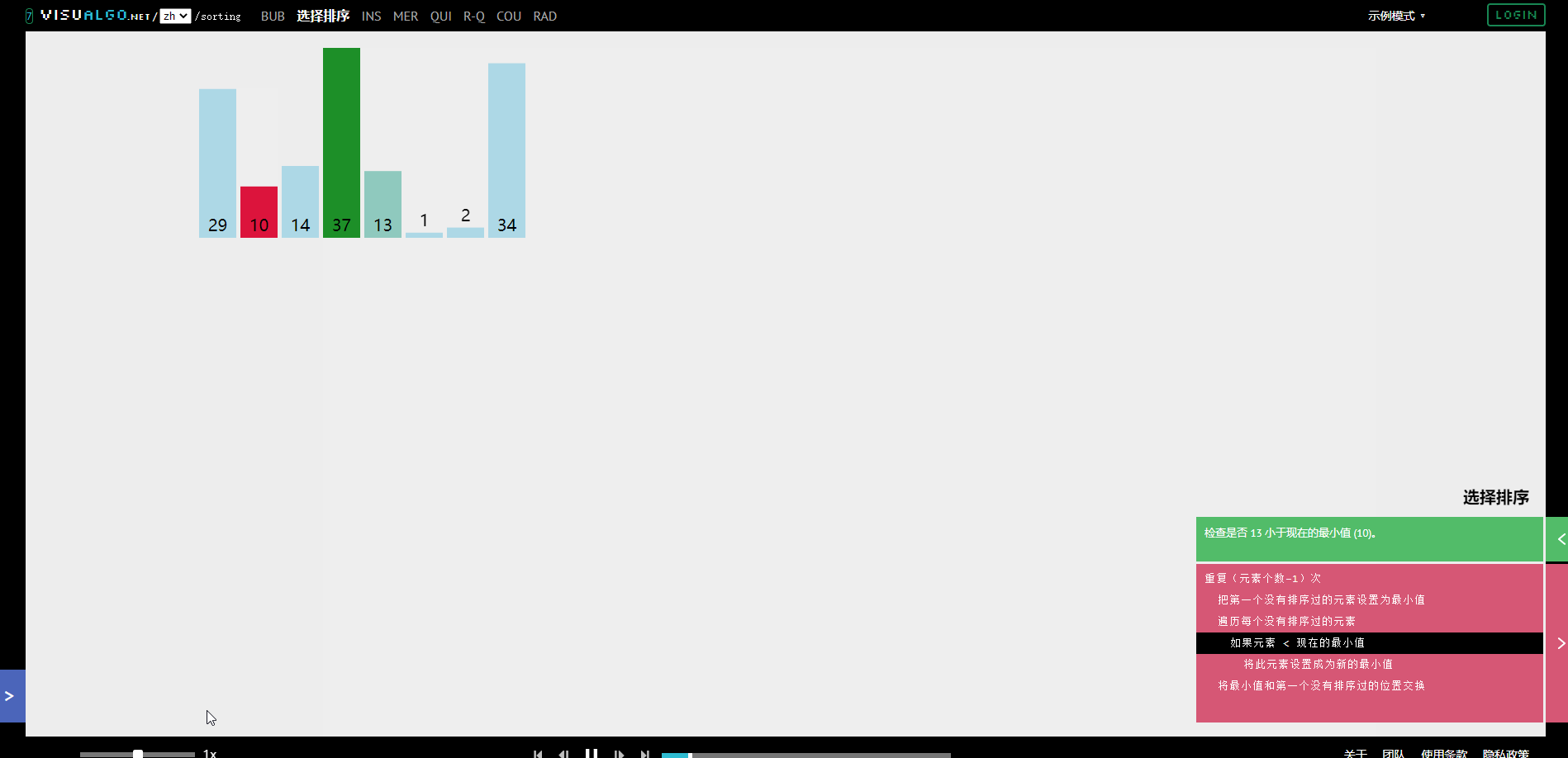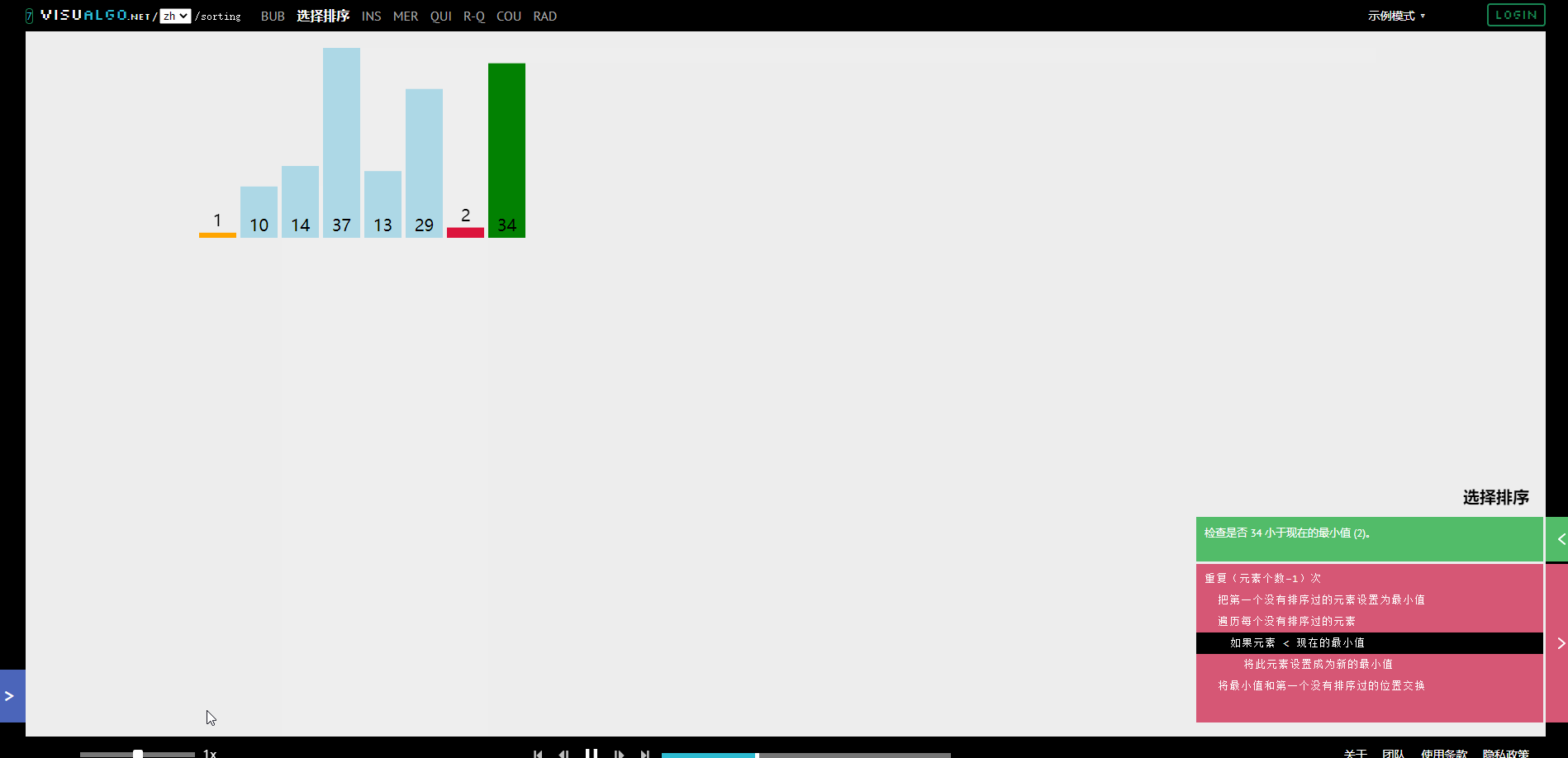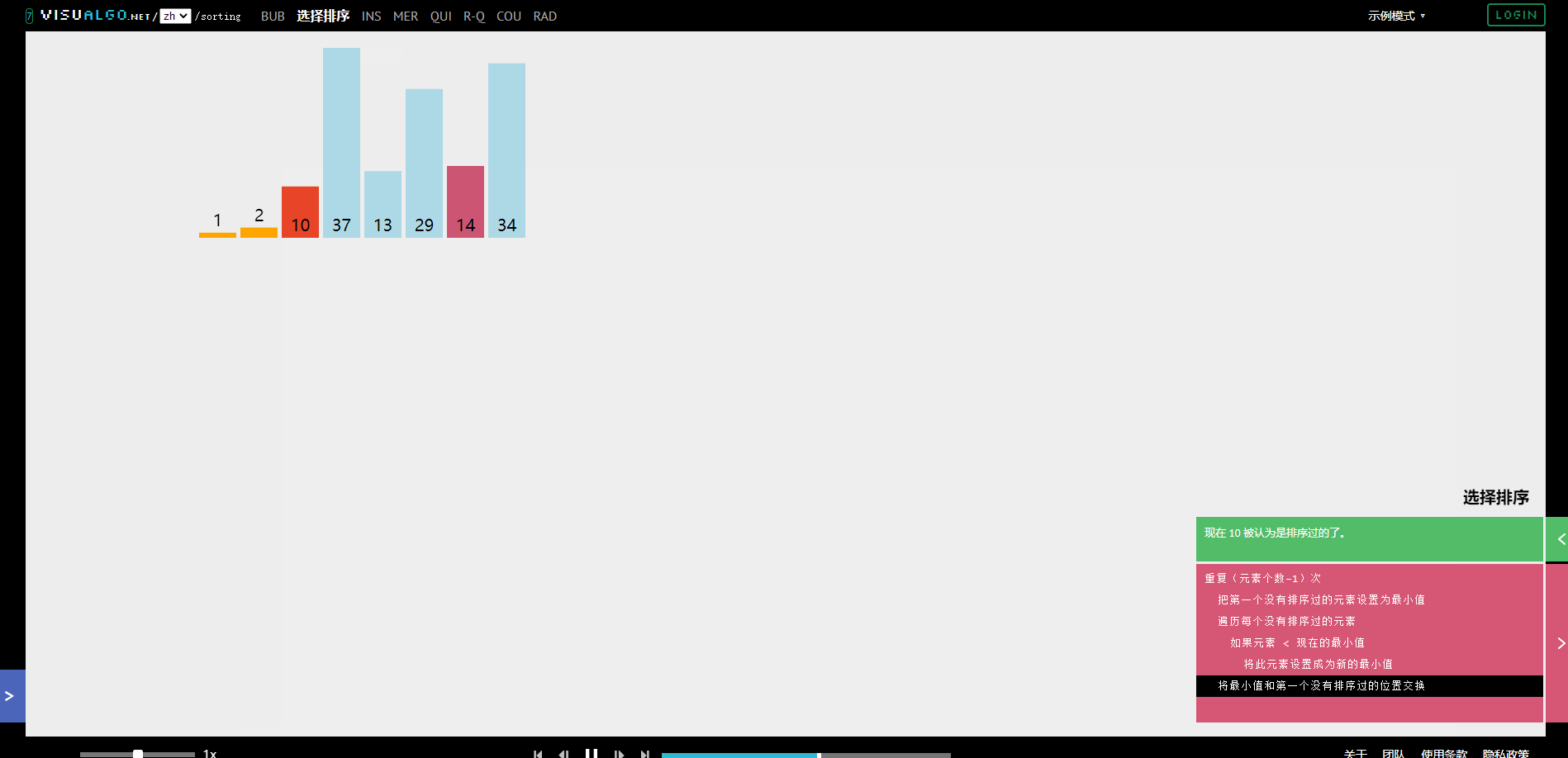
①.二项分布的最大似然估计
投硬币试验中,进行N次独立试验,n次朝上,N-n次朝下。
假定朝上的概率为p,使用对数似然函数作为目标函数:
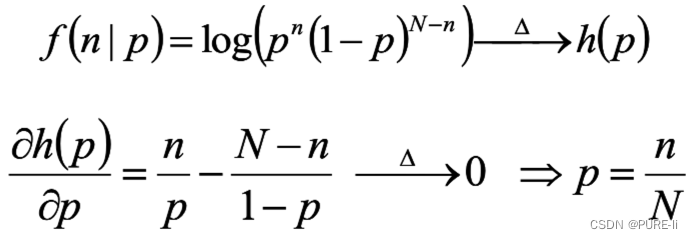
②.二项分布与先验举例
在校门口统计一定时间段内出入的男女生数目分别为NB和NG,估算该校男女生比例。若观察到4个女生和1个男生,可以得出该校女生比例是80%吗?
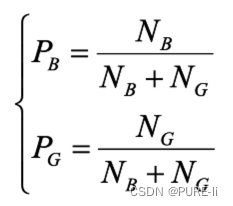

③.上述过程的理论解释
投掷一个非均匀硬币,可以使用参数为θ的伯努利模型,θ为硬币为正面的概率,那么结果x的分布形式为:![]()
两点分布/二项分布的共轭先验是Beta分布,它具有两个参数α和β,Beta分布形式为
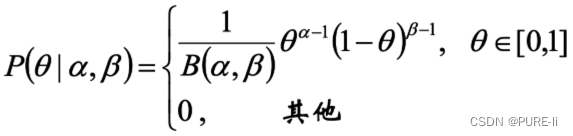
④.先验概率和后验概率的关系

后验概率是参数为(k+α,n-k+β)的Beta分布,即:伯努利分布/二项分布的共轭先验是Beta分布。
⑤.伪计数
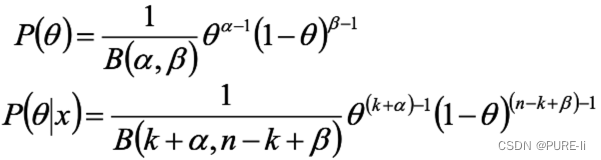
参数α、β是决定参数θ的参数,即超参数。
在后验概率的最终表达式中,参数α、β和k、n-k一起作为参数θ的指数——后验概率的参
数为(k+α,n-k+β)。
根据这个指数的实践意义:投币过程中,正面朝上的次数,α和β先验性的给出了在没有任何实验的前提下,硬币朝上的概率分配;因此,α和β可被称作“伪计数”。
⑥.共轭先验的直接推广
从2到K:
二项分布 到 多项分布
Beta分布 到 Dirichlet分布
2.Dirichlet分布
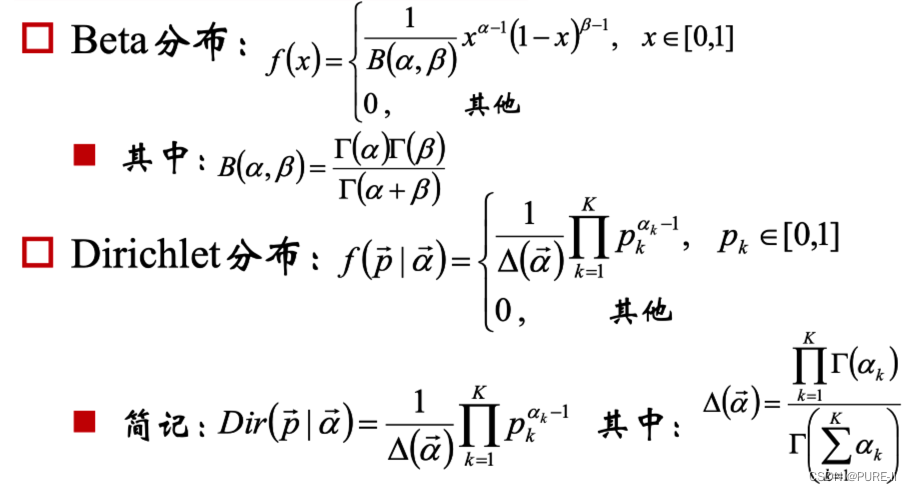
①.Dirichlet分布的期望
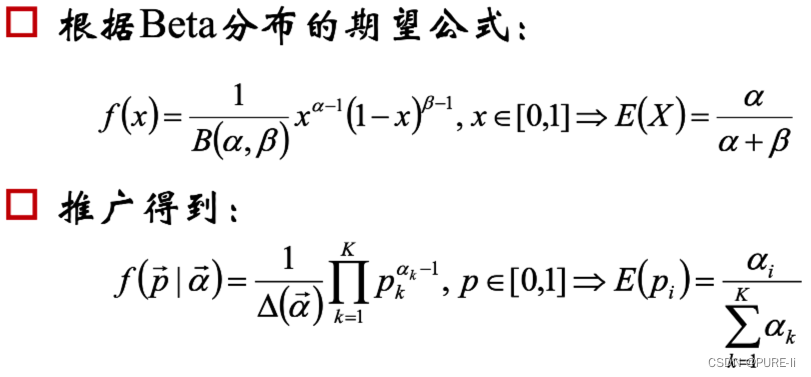
②.Dirichlet分布分析
![]()
α是参数向量,共K个
定义在x1,x2…xK-1维上
x1+x2+…+xK-1+xK=1
x1,x2…xK-1>0
定义在(K-1)维的单纯形上,其他区域的概率密度为0
α的取值对Dir(p|α)有什么影响?
③.对称Dirichlet分布

④.对称Dirichlet分布的参数分析
α=1时
退化为均匀分布
当α>1时
p1=p2=…=pk的概率增大
当α<1时
pi=1,p非i=0的概率增大
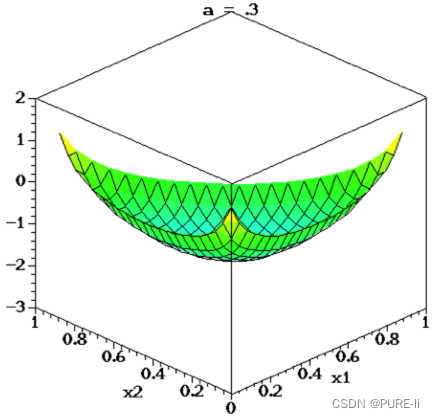

⑤.参数α对Dirichlet分布的影响

多项分布的共轭分布是Dirichlet分布
3.LDA模型
①.LDA的解释
1.共有m篇文章,一共涉及了K个主题;
2.每篇文章(长度为Nm)都有各自的主题分布,主题分布是多项分布,该多项分布的参数服从Dirichlet分布,该Dirichlet分布的参数为α;
3.每个主题都有各自的词分布,词分布为多项分布,该多项分布的参数服从Dirichlet
分布,该Dirichlet分布的参数为β;
4.对于某篇文章中的第n个词,首先从该文章的主题分布中采样一个主题,然后在这个主题对应的词分布中采样一个词。不断重复这个随机生成过程,直到m篇文章全部完成上述过程。
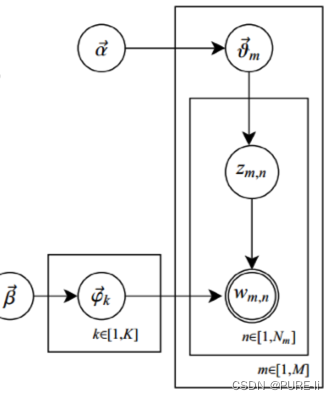
②.详细解释

图中K为主题个数,M为文档总数,Nm是第m个文档的单词总数。β是每个Topic下词的多项分布的Dirichlet先验参数,α是每个文档下Topic的多项分布的Dirichlet先验参数。zmn是第m个文档中第n个词的主题,wmn是m个文档中的第n个词。两个隐含变量θ和φ分别表示第m个文档下的Topic分布和第k个Topic下词的分布,前者是k维(k为Topic总数)向量,后者是v维向量(v为词典中term总数)
③.参数的学习
给定一个文档集合,wmn是可以观察到的已知变量,α和β是根据经验给定的先验参数,其他的变量zmn、θ、φ都是未知的隐含变量,需要根据观察到的变量来学习估计的。根据LDA的图模型,可以写出所有变量的联合分布:
![]()
④.似然概率
一个词wmn初始化为一个词t的概率是

每个文档中出现主题k的概率乘以主题k下出现词t的概率,然后枚举所有主题求和得到。整个文档集合的似然函数为:
![]()
4.Gibbs采样算法学习参数

①.联合分布
![]()
第一项因子是给定主题采样词的过程

②.计算因子
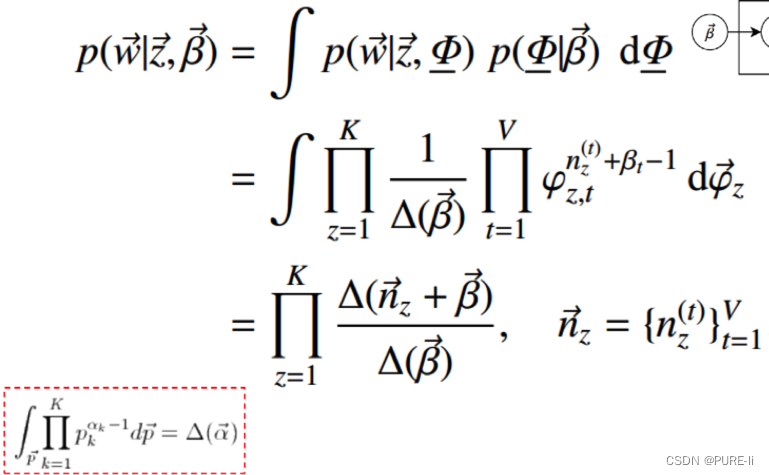
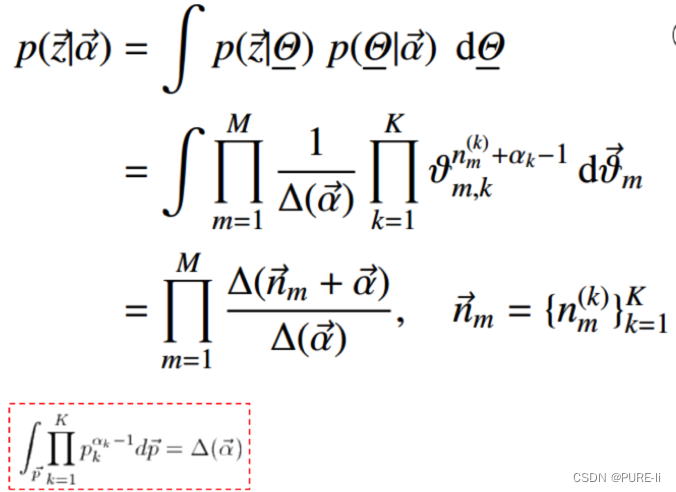

③.词分布和主题分布
七.代码实现
数目:
文档数目:M
词数目:V(非重复的,“term”)
主题数目:K
记号:
用d表述第几个文档,k表示主题,w表示词汇(term),n表示词(word)
八.三个矩阵和三个向量
z[d][w]:第d篇文档的第w个词来自哪个主题。M行,X列,X为相应文档长度:即词(可重复)的数目。
nw[w][t]:第w个词是第t个主题的次数。word-topic矩阵,列向量nw[][t]表示主题t的词频数分布;V行K列
nd[d][t]:第d篇文档中第t个主题出现的次数,doc-topic矩阵,行向量nd[d]表示文档d的主题频数分布。M行,K列。
辅助向量:
ntSum[t]:第t个主题在所有语料出现的次数,K维
ndSum[d]:第d篇文档中词的数目(可重复),M维;
P[t]:对于当前计算的某词属于主题t的概率,K维。
九.数据处理流程
1.获取QQ群聊天记录:txt文本格式(图1)
2.整理成“QQ号/时间/留言”的规则形式
正则表达式
清洗特定词:表情、@XX
使用停止词库
获得csv表格数据(图2)
3.合并相同QQ号的留言
长文档利于计算每人感兴趣话题(图3)
4.LDA模型计算主题
调参与可视化
5.计算每个QQ号及众人感兴趣话题
十.超参数的确定
交叉验证
α表达了不同文档间主题是否鲜明,β度量了有多少近义词能够属于同一个类别。
主题数目K,词项数目为W,可以使用:
α=50/K
β=200/W
注:不一定普遍适用
十一.一种迭代求超参数的方法
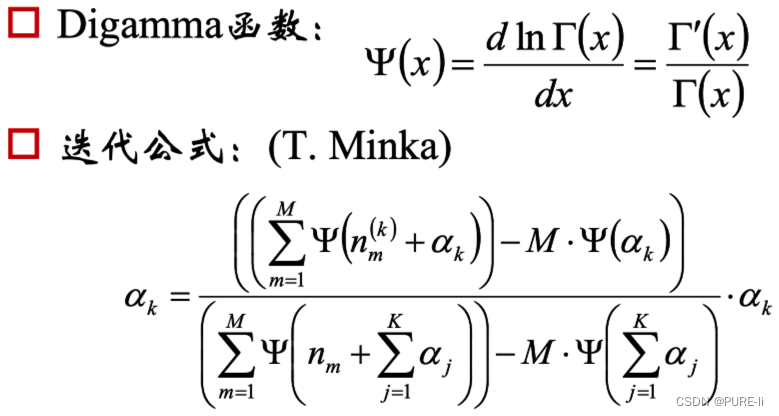
十二.主题个数的确定
相似度最小
选取初始的主题个数K,训练LDA模型,计算各主题之间的相似度
增加或减少K的值,重新训练LDA模型,再次计算topic之间的相似度
选择相似度最小的模型所对应的K作为主题个数。
十三.概率分布的困惑度/复杂度Perplexity
某离散概率分布p的困惑度为
![]()
样本集x1,x2…xn的估计模型q的困惑度为:
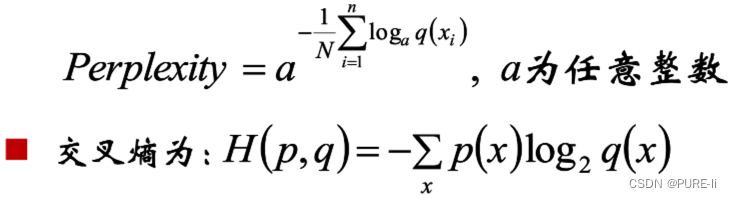
十四.困惑度Perplexity与主题模型
使用训练数据得到无监督模型,在测试数据集中计算所有token似然值几何平均数的倒数
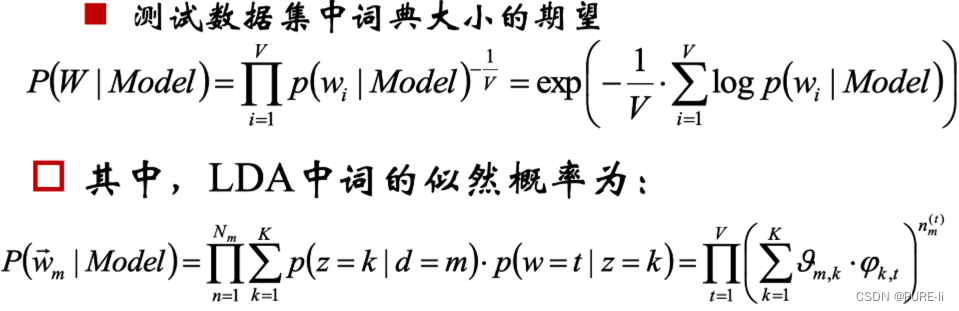
十五.PageRank
一个网页i的重要度可以使用指向网页i的其他网页j 的重要度加权得到。
权值不妨取网页j包含的链接数目。
![]()
参数的意义为:

十六.TextRank
将PageRank中的“网页”换成“词”,结论仍成立。
选择合适的窗口大小,认为窗口内的词相互指向。
![]()
句子Si和Sj的相似度:
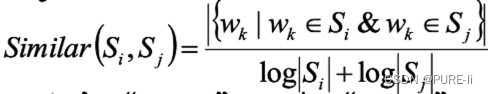
将PageRank中“网页”换成“句子”,结论仍然基本成立,只需考虑将“链接”加权:
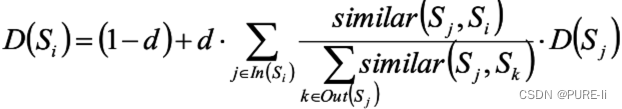
十七.LDA总结
由于在词和文档之间加入的主题的概念,可以较好的解决一词多义和多词一义的问题。
在实践中发现,LDA用于短文档往往效果不明显—— 这是可以解释的:因为一个词被分配给某个主题的次数和一个主题包括的词数目尚未敛。往往需要通过其他方案“连接”成长文档。
LDA可以和其他算法相结合。首先使用LDA将长度为Ni的文档降维到K维(主题的数目),同时给出每个主题的概率(主题分布),从而可以使用if-idf继续分析或者直接作为文档的特征进入聚类或者标签传播算法— —用于社区发现等问题。