1.技能升级

1.题目描述

小蓝最近正在玩一款 RPG 游戏。
他的角色一共有 $N$ 个可以加攻击力的技能。

其中第 $i$个技能首次升级可以提升 $A_i$点攻击力，以后每次升级增加的点数都会减少 $B_i$。$\lceil \frac{Ai}{Bi}\rceil$（上取整）次之后，再升级该技能将不会改变攻击力。

现在小蓝可以总计升级 $M$ 次技能，他可以任意选择升级的技能和次数。

请你计算小蓝最多可以提高多少点攻击力？

2.输入格式

输入第一行包含两个整数 $N$ 和 $M$。
以下 $N$ 行每行包含两个整数 $A_i$和 $B_i$。

3.输出格式

输出一行包含一个整数表示答案。

4.样例输入

3 6
10 5
9 2
8 1

5.样例输出

47

6.数据范围

$1\le N\le 10^5，1\le M\le 2\times 10^9，1\le Ai,Bi\le 10^6。$

7.原题链接

技能升级

2.解题思路

根据题意思考虑，每一个技能的提升点数都会是一个递减的等差序列，首项为 $a_i$，公差为 $b_i$，那么对于第 $i$ 个序列应为：
$$a_i，a_i-b_i，a_i-2b_i\dots ,a_i-\lceil \frac{a_i}{b_i}\rceil b_i$$
出于贪心考虑，我们每次将升级当前最大的 $a_i$，这样选够 $m$ 次一定为正确答案，所以我们可以使用优先队列模拟，这样的复杂度为 $O(mlogn)。$但 $m$ 最大值为 $2\times 10^9$，这样会TLE。

考虑完成所有选择以后，我们选择的情况一定如下图（红色表示已选），即每个技能一定在其头部选择了若干个元素，总共需要选够 $m$ 个元素，因为每个数组都是递减的，所以选择的所有元素一定是所有元素的前 $m$ 大的元素。那么这就是一个多路归并问题。

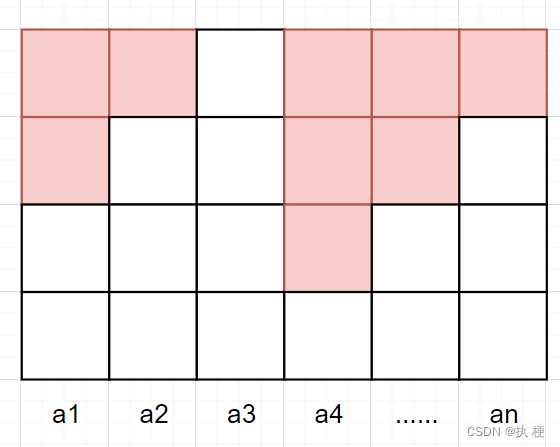
什么是多路归并呢，这里顾名思义就是直接将所有序列合起来，以题目样例举例：
技能1：$10$ $5$
技能2：$9$ $7$ $5$ $3$ $1$
技能3：$8$ $7$ $6$ $5$ $4$ $3$ $2$ $1$
我们将三个序列合并后按从大到小进行排序得到新序列 $H$:
$$H=[10,9,8,7,7,6,5,5,5,4,3,3,2,1,1]$$

样例的 $m$ 为 6，那么答案即为最大前6个元素之和，这就是多路归并的思想，由贪心可知这样的选择一定正确且我们可以通过在题目的要求下完成如此选法。但显然我们如果暴力存储然后排序仍会TLE，考虑如何去进行优化。

首先思考多路归并的数组对我们有什么作用？答案是我们可以求解得到我们选择的第 $m$ 个数是多少，定义 $f(x)$ 为所有数列中大于等于 $x$ 的数有多少个。

从$f(x)$的定义可知，若某个值 $t$ 满足$f(t)=m$，那么数列中所有大于等于 $t$ 的数恰好就是前 $m$ 大的数。又可知当$x<y$时，一定满足 $f(x)\ge f(y)$，所以当 $x$ 满足$f(x)\ge m$时，$x-1$也一定满足，而$x+1$却不一定满足，由此符合二段性，所以我们可以去二分求解得到 $t$，其实就是求满足 $f(x)\ge m$ 的最大值。

比如样例中二分求得的 $t$ 就是 6，因为 $f(6)=m$，那么我们把所有大于等于6的数都选上即是答案。

但是已知 $x$，如何求得$f(x)$？对于第 $i$ 个数列，我们可以选择的个数为 $(a_i-x)/b_i+1$，那么对于任意一个 $x$ 我们都可以在$O(n)$的时间复杂度求得 $f(x)$。加上我们二分的复杂度为 $O(logn)$，那么我们可以在$O(nlogn)$的复杂度求解得到 $t$。

得到 $t$ 之后就简单了，我们只需要把每个数列中大于等于 $t$ 的值都选上即可。这也很好求解，由于是等差数列，那么每个数组可选的个数为 $(a_i-t)/b_i+1$，首项为 $a_i$，那么末项为 $a_i-(c-1)\ast b_i$，已知首项末项以及项数，根据等差数列求和公式 $S=\frac{n}{2}(a_1+a_n)$可以求出每一列我们选的总和。

需要注意的是，我们求解的 $t$ 是满足 $f(t)>=m$并不一定恰好是 $f(t)=m$，因为原数列中可能有多个 $t$，我们可能会选多，所以还需要记录下我们总共选了多少个数，最后减去多余的 $t$。比如如果样例中存在两个6，那么我们就会选到7个数，需要减去一个6。
时间复杂度:$O(nlogn)$

3Ac_code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 200010;

LL n, m;
void solve()
{
	cin >> n >> m;
	std::vector<LL> a(n), b(n);
	for (int i = 0; i < n; ++i) cin >> a[i] >> b[i];
	auto check = [&](int x) {
		LL s = 0;
		for (int i = 0; i < n; ++i) {
			if (a[i] >= x) s += (a[i] - x) / b[i] + 1;
		}
		return s >= m;
	};
	int l = 0, r = 1e6;
	while (l < r) {
		int mid = l + r + 1 >> 1;
		if (check(mid)) l = mid;
		else r = mid - 1;
	}
	LL ans = 0, cnt = 0;
	for (int i = 0; i < n; ++i) {
		if (a[i] >= r) {
			//可取个数
			LL c = (a[i] - r) / b[i] + 1;
			//末项
			LL end = a[i] - (c - 1) * b[i];
			//求和
			ans += (a[i] + end) * c / 2;
			cnt += c;
		}
	}
	ans -= (cnt - m) * r;
	cout << ans << '\n';
}
int main()
{
	ios_base :: sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	int t = 1;
	while (t--)
	{
		solve();
	}
	return 0;
}