一、试除法求n的所有约数

vector<int> getDivisors(int n) {
	vector<int> ans;
	for (int i = 2; i <= n / i; i++) {
		if (n % i == 0) {
			ans.push_back(i);
			if (i != n / i) {
				ans.push_back(n / i); // n == n/i，只需要存一个
			}
		}
	}
	return ans;
}

时间复杂度：$O(\sqrt{n})$

二、约数个数

约数和质因子并不是一个意思，但每个约数可以表示成质因子的乘积

算数基本定理：$n=p_1^{c_1}\ast p_2^{c_2}\ast ...\ast p_k^{c_k}$的约数个数为：$(c_1+1)(c_2+1)\dots (c_k+1)$，$p_k$为质因子

例子：$12=2^2\times 3^1$，12的约数有1,2,3,4,6,12共6个，根据公式计算同样是$(2+1)\times (1+1)=6$个

n的每个约数m都可以表示成$m=p_1^{b_1}\ast p_2^{b_2}\ast ...\ast p_k^{b_k}$的形式，$0<=b_k<=c_k$，每个$b_k$有$(c_k+1)$种选法，于是就有$(c_1+1)(c_2+1)\dots (c_k+1)$个因数

我们分解质因子后，获取质因子的指数，最后套用$(c_1+1)(c_2+1)\dots (c_k+1)$即可

int getDivisorsNum(int n) {
	vector<int> nums;
	for (int i = 2; i <= n / i; i++) {
		if (n % i == 0) {
			int num = 0;
			while (n % i == 0) {
				n /= i;
				num++;
			}
			// 获取质因子的指数
			nums.push_back(num);
		}
	}
	if(n > 1) nums.push_back(1);
	int ans = 1;
	for (int num : nums) {
		ans *= (num + 1);
	}
	return ans;
}

三、约数之和

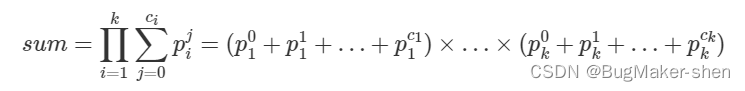
例子：$12=2^2\times 3^1$，12的约数有1,2,3,4,6,12，约数之和为28，根据公式计算同样是$(2^0+2^1+2^2)\times (3^0+3^1)=28$个

其中，$p^0+p^1+p^2+...+p^n=(((p+1)\times p+1)\times p+1...)+1$，一直循环n次

int getDivisorsSum(int n) {
	const int mod = 1e9 + 7;
	unordered_map<int, int> primes;
	for (int i = 2; i <= n / i; i++) {
		if (n % i == 0) {
			while (n % i == 0) {
				n /= i;
				primes[i]++;
			}
		}
	}
	if (n > 1) primes[n] = 1;
	
	long long ans = 1;
	for (auto prime : primes) {
		int p = prime.first;
		int n = prime.second;
		// 计算sum = p^0 + p^1 + p^2 + ... + p^n
		long long sum = 1;
		while (n >= 1) {
			sum = (sum * p + 1) % mod;
			n--;
		}
		ans = ans * sum % mod;
	}
	return ans;
}

四、最大公约数（欧几里得算法/辗转相除法）

如果d是a的约数，也是b的约数，则d是ax+by的约数，则有：$gcd(a,b)=gcd(b,a\%b)$，$gcd(a,0)=a$

比如a=24，b=18，那么gcd(24,18)=6，gcd(18,24%18)=6

int gcd(int a, int b) {
	return b ? gcd(b, a % b) : a;
}

时间复杂度为$O(logn)$