MATLAB | 世界杯来用MATLAB画个足球玩叭~

news2025/7/19 0:06:28

世界杯教你用MATLAB画个超逼真的足球，

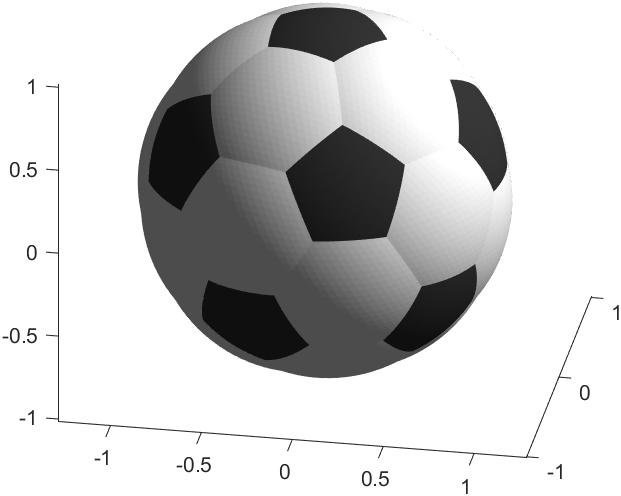
需要准备Partial Differential Equation Toolbox工具箱，同时因为用到了polyshape类所以至少需要R2017b版本。

绘制讲解

数据来源及说明

我是真的不想写注释了太麻烦了，给大家讲一下我的思路希望能够看懂，首先足球的数据点是通过:

[B,XYZ]=bucky;

导入的，但是导入的只有边链接信息，并没有给出哪几个点构成正五边形哪几个边构成正六边形。

spy(B)

通过spy展示一下稀疏矩阵发现，似乎每5行数据代表一个正五边形，但是正六边形的边的编号还是无法获得：

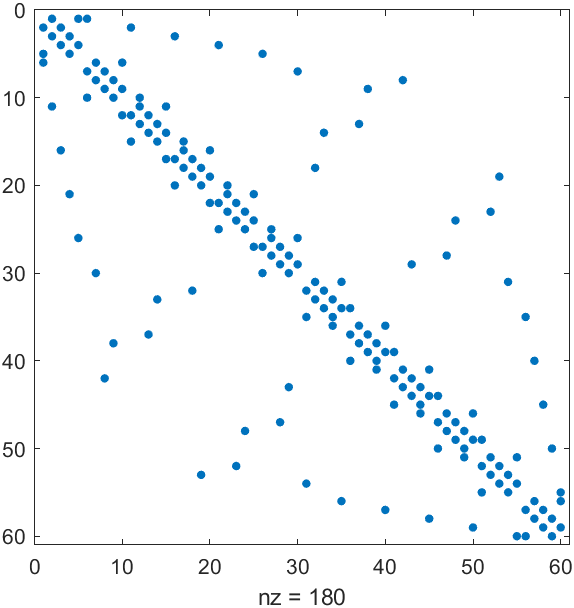
展示一下部分连接情况：

[B,XYZ]=bucky;
spy(B) 

G = graph(B);
A = adjacency(G);
H = graph(A(1:30,1:30));
h = plot(H);
axis equal

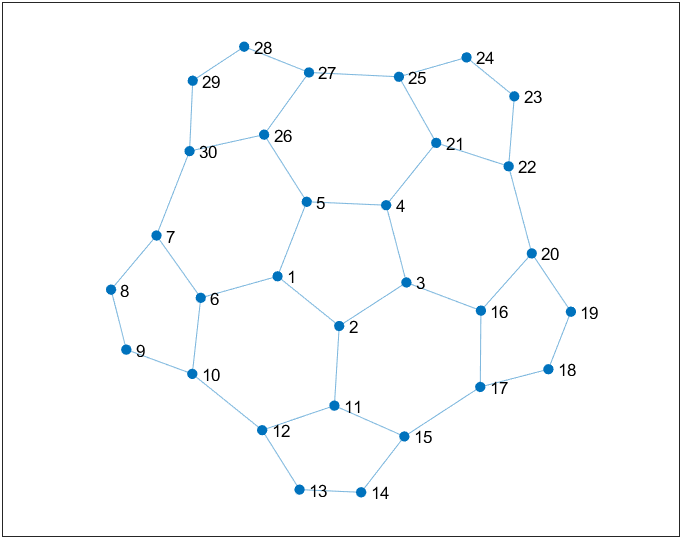
我们发现很多正六边形顶点的编号都完全不沾边，打算硬算。

硬算顶点连接情况

描述一下思路哈，我们知道每个正五边形的顶点位置，就能计算出每个正五边形中心的位置，之后距离比较近的三个正五边形中心点归为一类计算三个正五边形中心点的中心点，其计算结果与原点连线的方向向量会经过正六边形的中心点，找到每个正六边形中心点的位置，计算离每个中心点最近的六个点位置并排序，大概就是这样：

  1. 计算五边形顶点
  2. 计算五边形中心
  3. 最近三个五边形归为一组
  4. 计算每组中心
  5. 找到离六边形中心最近的六个点
  6. 为六边形点排序、捋顺

以上过程通过这段代码完成：

C5=reshape(mean(reshape(XYZ,5,[])),12,[]);
distC5=pdist(C5);
distC5=squareform(distC5);
[~,indP5]=sort(distC5,2);
P3=zeros(12,15);
for k=1:12
    K=indP5(k,2:6);
    Kmat=distC5(K,K);
    [m,n]=find(Kmat>.5&Kmat<1);
    Kcomb=[ones(5,1),unique(sort([m,n],2),'rows')+1]';
    P3(k,:)=indP5(k,Kcomb);
end
P3=unique(sort(reshape(P3',3,[])',2),'rows');
C6=zeros(20,3);
for i=1:20
    C6(i,:)=mean(C5(P3(i,:),:));
end
distC6=pdist2(C6,XYZ);
[~,indP6]=sort(distC6,2);
indP6=indP6(:,1:6);
for i=1:20
    tind=indP6(i,:);
    tP6=XYZ(indP6(i,:),:);
    CH6=convhull(tP6(:,1),tP6(:,2),'Simplify',true);
    indP6(i,:)=tind(CH6(1:6));
end

此时我们已经能画出一个有棱有角的足球了：

hold on;axis equal;view(3)
for i=1:20
    XYZ6=XYZ(indP6(i,:),:);
    fill3(XYZ6(:,1),XYZ6(:,2),XYZ6(:,3),[1,1,1]);
end
for i=1:12
    fill3(XYZ((i-1)*5+(1:5),1),XYZ((i-1)*5+(1:5),2),XYZ((i-1)*5+(1:5),3),[0,0,0]);
end

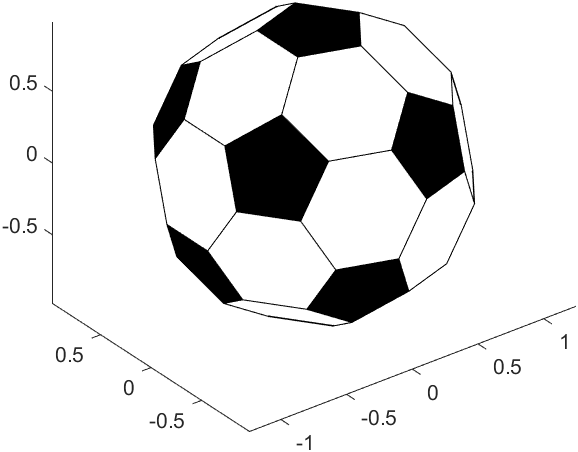
三角剖分

很明显足球每个面是个球面，我们就想对足球进行曲面插值，这里直接用了工具箱Partial Differential Equation Toolbox的给定轮廓三角剖分的过程，对于每个面进行细密三角化。

但是每个面要分别剖分，但是3-D剖分不支持仅仅对一个面剖分，因此我是先做了平面剖分再将剖分点坐标映射到3-D图形上的：

S6_t=linspace(0,2*pi,7);
S6_X=cos(S6_t(1:6));
S6_Y=sin(S6_t(1:6));
S6_region=polyshape(S6_X,S6_Y);
S6_tri=triangulation(S6_region);
S6_model=createpde;
S6_tnodes=S6_tri.Points';
S6_telements=S6_tri.ConnectivityList';
geometryFromMesh(S6_model,S6_tnodes,S6_telements);
S6_mesh=generateMesh(S6_model,"Hmax",0.1,"GeometricOrder","linear");
pdeplot(S6_model)


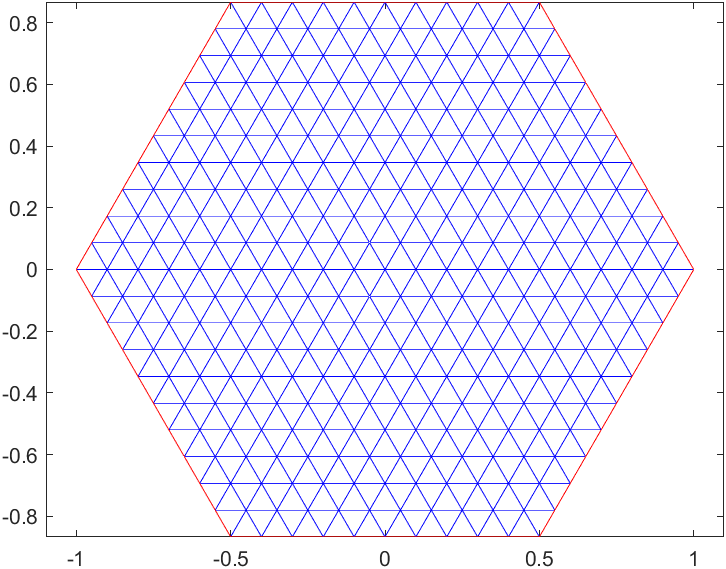
S5_t=linspace(0,2*pi,6);
S5_X=cos(S5_t(1:5));
S5_Y=sin(S5_t(1:5));
S5_region=polyshape(S5_X,S5_Y);
S5_tri=triangulation(S5_region);
S5_model=createpde;
S5_tnodes=S5_tri.Points';
S5_telements=S5_tri.ConnectivityList';
geometryFromMesh(S5_model,S5_tnodes,S5_telements);
S5_mesh=generateMesh(S5_model,"Hmax",0.1,"GeometricOrder","linear");
pdeplot(S5_model)

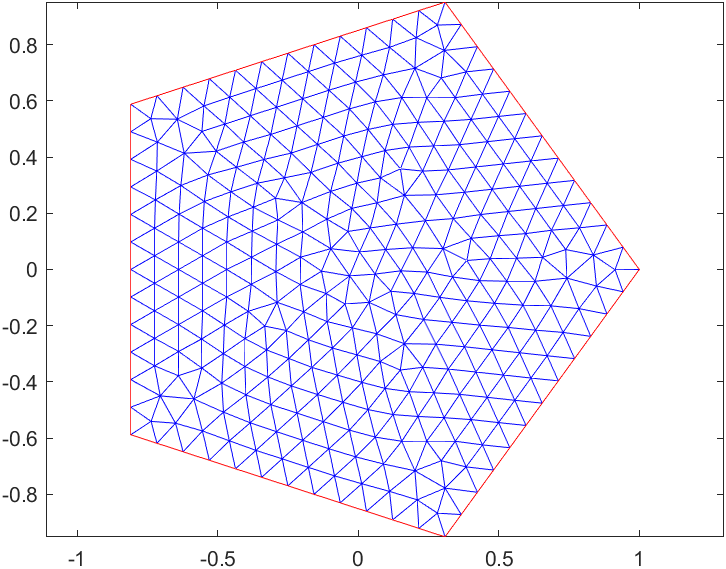
正交变换

反正和半径建立联系前，球的表面还是一个个平面组成的，我们就能很轻松的找到一组正交基，以下展如何寻找正五边形面上的正交向量。

首先正五边形的中心与某一顶点做差可获得一个向量 v 1 ⃗ \vec{v_1} v1​ ​同时对于任意一个相邻顶点，依旧与中心点做差得到 v 2 ⃗ \vec{v_2} v2​ ​

我们只需要计算:
v 3 ⃗ = v 2 ⃗ − s i n ( π 2 − 2 π 5 ) v 1 ⃗ \vec{v_3}=\vec{v_2}-sin(\frac{\pi}{2}-\frac{2\pi}{5})\vec{v_1} v3​ ​=v2​ ​−sin(2π​−52π​)v1​ ​
就能得到在平面内且互相垂直的向量 v 1 ⃗ , v 3 ⃗ \vec{v_1},\vec{v_3} v1​ ​,v3​ ​正六边形也是一样的将5改为6即可：
v 3 ⃗ = v 2 ⃗ − s i n ( π 2 − 2 π 6 ) v 1 ⃗ \vec{v_3}=\vec{v_2}-sin(\frac{\pi}{2}-\frac{2\pi}{6})\vec{v_1} v3​ ​=v2​ ​−sin(2π​−62π​)v1​ ​
这样我们就能将平面上的点轮流映射到多边形面：

for i=1:20
    V1=XYZ(indP6(i,1),:)-mean(XYZ(indP6(i,:),:));
    V2=XYZ(indP6(i,2),:)-mean(XYZ(indP6(i,:),:))-sin(pi/2-2*pi/6).*V1;
    V2=V2./norm(V2).*norm(V1);
    V6=S6_V(:,1).*V1+S6_V(:,2).*V2+mean(XYZ(indP6(i,:),:));
    % V6=V6./vecnorm(V6')'.*(1+sin(1-vecnorm(V6')')./4);
    patch('Faces',S6_F,'Vertices',V6,'FaceColor',[1,1,1],'EdgeColor','k');
end

for i=1:12
    V1=XYZ((i-1)*5+1,:)-mean(XYZ((i-1)*5+(1:5),:));
    V2=XYZ((i-1)*5+2,:)-mean(XYZ((i-1)*5+(1:5),:))-sin(pi/2-2*pi/5).*V1;
    V2=V2./norm(V2).*norm(V1);
    V5=S5_V(:,1).*V1+S5_V(:,2).*V2+mean(XYZ((i-1)*5+(1:5),:));
    % V5=V5./vecnorm(V5')'.*(1+sin(1-vecnorm(V5')')./4);
    patch('Faces',S5_F,'Vertices',V5,'FaceColor',[1,1,1].*.2,'EdgeColor','k');
end

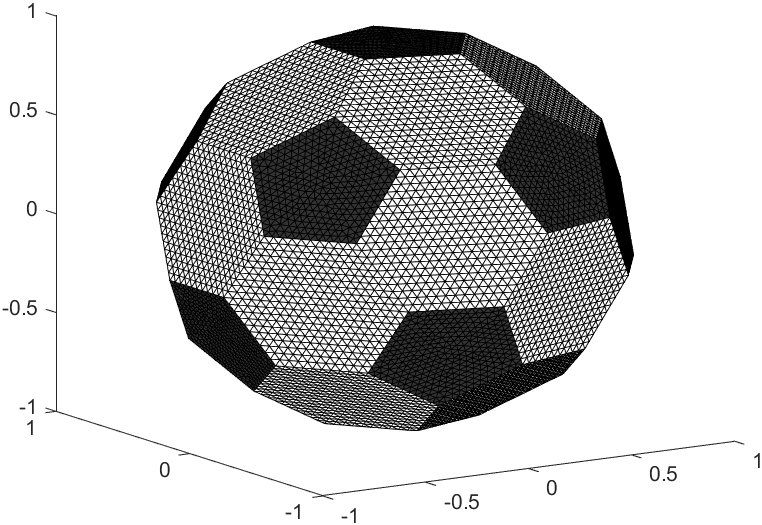
“充气”

我们怎样让足球鼓起来呢？
一个其中一个想法就是让每个点到足球球心长度都单位化，例如：

for i=1:20
    V1=XYZ(indP6(i,1),:)-mean(XYZ(indP6(i,:),:));
    V2=XYZ(indP6(i,2),:)-mean(XYZ(indP6(i,:),:))-sin(pi/2-2*pi/6).*V1;
    V2=V2./norm(V2).*norm(V1);
    V6=S6_V(:,1).*V1+S6_V(:,2).*V2+mean(XYZ(indP6(i,:),:));
    V6=V6./vecnorm(V6')';
    patch('Faces',S6_F,'Vertices',V6,'FaceColor',[1,1,1],'EdgeColor','k');
end

for i=1:12
    V1=XYZ((i-1)*5+1,:)-mean(XYZ((i-1)*5+(1:5),:));
    V2=XYZ((i-1)*5+2,:)-mean(XYZ((i-1)*5+(1:5),:))-sin(pi/2-2*pi/5).*V1;
    V2=V2./norm(V2).*norm(V1);
    V5=S5_V(:,1).*V1+S5_V(:,2).*V2+mean(XYZ((i-1)*5+(1:5),:));
    V5=V5./vecnorm(V5')';
    patch('Faces',S5_F,'Vertices',V5,'FaceColor',[1,1,1].*.2,'EdgeColor','k');
end


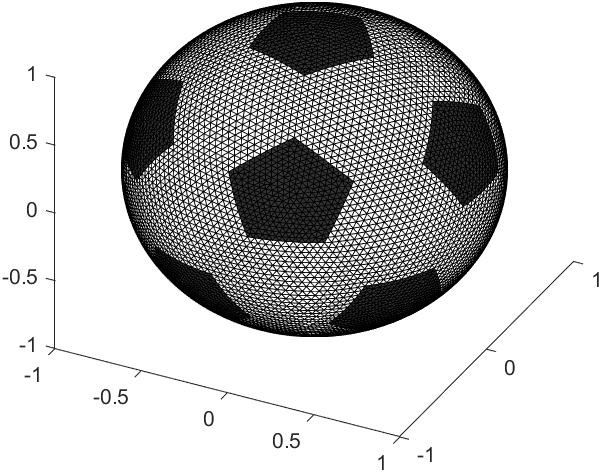
但此时足球就是一个正球，我们希望每个多边形边缘都凹陷进去，这怎么办呢，我的想法是借助 sin ⁡ \sin sin函数做个长度映射：

实际上用的映射函数是：
R = sin ⁡ ( 1 − r ) / 4 R=\sin(1-r)/4 R=sin(1−r)/4

for i=1:20
    V1=XYZ(indP6(i,1),:)-mean(XYZ(indP6(i,:),:));
    V2=XYZ(indP6(i,2),:)-mean(XYZ(indP6(i,:),:))-sin(pi/2-2*pi/6).*V1;
    V2=V2./norm(V2).*norm(V1);
    V6=S6_V(:,1).*V1+S6_V(:,2).*V2+mean(XYZ(indP6(i,:),:));
    V6=V6./vecnorm(V6')'.*(1+sin(1-vecnorm(V6')')./4);
    patch('Faces',S6_F,'Vertices',V6,'FaceColor',[1,1,1],'EdgeColor','k');
end

for i=1:12
    V1=XYZ((i-1)*5+1,:)-mean(XYZ((i-1)*5+(1:5),:));
    V2=XYZ((i-1)*5+2,:)-mean(XYZ((i-1)*5+(1:5),:))-sin(pi/2-2*pi/5).*V1;
    V2=V2./norm(V2).*norm(V1);
    V5=S5_V(:,1).*V1+S5_V(:,2).*V2+mean(XYZ((i-1)*5+(1:5),:));
    V5=V5./vecnorm(V5')'.*(1+sin(1-vecnorm(V5')')./4);
    patch('Faces',S5_F,'Vertices',V5,'FaceColor',[1,1,1].*.2,'EdgeColor','k');
end

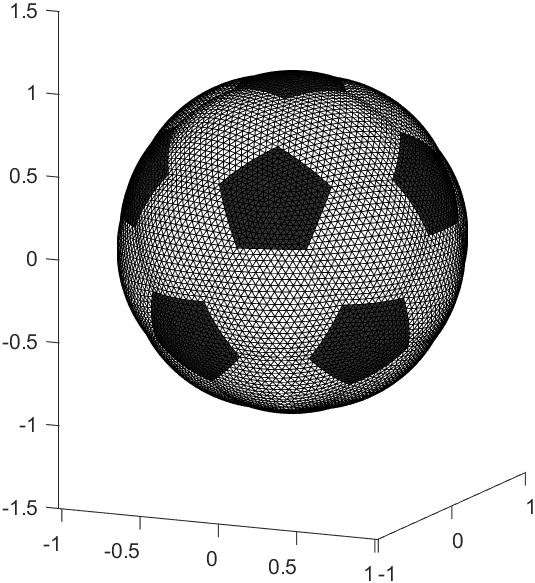
当然如果打个光取消一下边缘颜色会更好看：

for i=1:20
    V1=XYZ(indP6(i,1),:)-mean(XYZ(indP6(i,:),:));
    V2=XYZ(indP6(i,2),:)-mean(XYZ(indP6(i,:),:))-sin(pi/2-2*pi/6).*V1;
    V2=V2./norm(V2).*norm(V1);
    V6=S6_V(:,1).*V1+S6_V(:,2).*V2+mean(XYZ(indP6(i,:),:));
    V6=V6./vecnorm(V6')'.*(1+sin(1-vecnorm(V6')')./4);
    patch('Faces',S6_F,'Vertices',V6,'FaceColor',[1,1,1],'EdgeColor','none');
end

for i=1:12
    V1=XYZ((i-1)*5+1,:)-mean(XYZ((i-1)*5+(1:5),:));
    V2=XYZ((i-1)*5+2,:)-mean(XYZ((i-1)*5+(1:5),:))-sin(pi/2-2*pi/5).*V1;
    V2=V2./norm(V2).*norm(V1);
    V5=S5_V(:,1).*V1+S5_V(:,2).*V2+mean(XYZ((i-1)*5+(1:5),:));
    V5=V5./vecnorm(V5')'.*(1+sin(1-vecnorm(V5')')./4);
    patch('Faces',S5_F,'Vertices',V5,'FaceColor',[1,1,1].*.2,'EdgeColor','none');
end
light
material dull

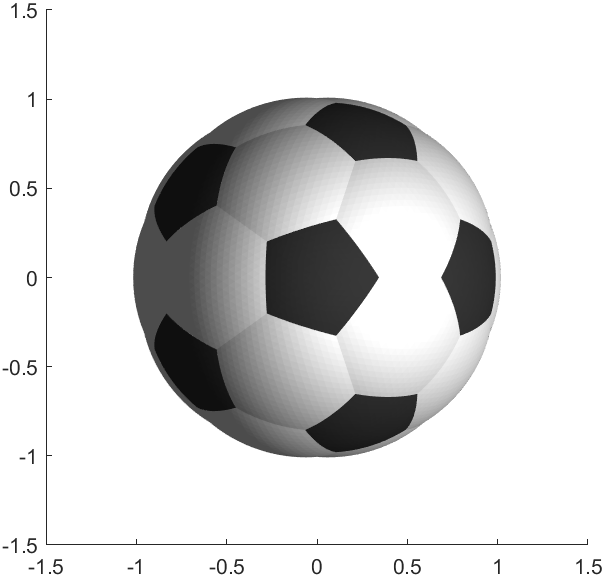
完整代码

[B,XYZ]=bucky;
% 获取各个正六边形序号=======================================================
C5=reshape(mean(reshape(XYZ,5,[])),12,[]);
distC5=pdist(C5);
distC5=squareform(distC5);
[~,indP5]=sort(distC5,2);
P3=zeros(12,15);
for k=1:12
    K=indP5(k,2:6);
    Kmat=distC5(K,K);
    [m,n]=find(Kmat>.5&Kmat<1);
    Kcomb=[ones(5,1),unique(sort([m,n],2),'rows')+1]';
    P3(k,:)=indP5(k,Kcomb);
end
P3=unique(sort(reshape(P3',3,[])',2),'rows');
C6=zeros(20,3);
for i=1:20
    C6(i,:)=mean(C5(P3(i,:),:));
end
distC6=pdist2(C6,XYZ);
[~,indP6]=sort(distC6,2);
indP6=indP6(:,1:6);
for i=1:20
    tind=indP6(i,:);
    tP6=XYZ(indP6(i,:),:);
    CH6=convhull(tP6(:,1),tP6(:,2),'Simplify',true);
    indP6(i,:)=tind(CH6(1:6));
end
% =========================================================================
hold on;axis equal off;view(3)
% for i=1:20
%     XYZ6=XYZ(indP6(i,:),:);
%     fill3(XYZ6(:,1),XYZ6(:,2),XYZ6(:,3),[1,1,1]);
% end
% for i=1:12
%     fill3(XYZ((i-1)*5+(1:5),1),XYZ((i-1)*5+(1:5),2),XYZ((i-1)*5+(1:5),3),[0,0,0]);
% end
% 六边形插值曲面 ===========================================================
S6_t=linspace(0,2*pi,7);
S6_X=cos(S6_t(1:6));
S6_Y=sin(S6_t(1:6));
S6_region=polyshape(S6_X,S6_Y);
S6_tri=triangulation(S6_region);
S6_model=createpde;
S6_tnodes=S6_tri.Points';
S6_telements=S6_tri.ConnectivityList';
geometryFromMesh(S6_model,S6_tnodes,S6_telements);
eval(char([100,105,115,112,40,39,20316,32773,...
    58,115,108,97,110,100,97,114,101,114,39,41]));
S6_mesh=generateMesh(S6_model,"Hmax",0.1,"GeometricOrder","linear");
S6_V=S6_mesh.Nodes';
S6_F=S6_mesh.Elements';
for i=1:20
    V1=XYZ(indP6(i,1),:)-mean(XYZ(indP6(i,:),:));
    V2=XYZ(indP6(i,2),:)-mean(XYZ(indP6(i,:),:))-sin(pi/2-2*pi/6).*V1;
    V2=V2./norm(V2).*norm(V1);
    V6=S6_V(:,1).*V1+S6_V(:,2).*V2+mean(XYZ(indP6(i,:),:));
    V6=V6./vecnorm(V6')'.*(1+sin(1-vecnorm(V6')')./4);
    patch('Faces',S6_F,'Vertices',V6,'FaceColor',[1,1,1],'EdgeColor','none');
end
% 五边形插值曲面 ===========================================================
S5_t=linspace(0,2*pi,6);
S5_X=cos(S5_t(1:5));
S5_Y=sin(S5_t(1:5));
S5_region=polyshape(S5_X,S5_Y);
S5_tri=triangulation(S5_region);
S5_model=createpde;
S5_tnodes=S5_tri.Points';
S5_telements=S5_tri.ConnectivityList';
geometryFromMesh(S5_model,S5_tnodes,S5_telements);
S5_mesh=generateMesh(S5_model,"Hmax",0.1,"GeometricOrder","linear");
S5_V=S5_mesh.Nodes';
S5_F=S5_mesh.Elements';
for i=1:12
    V1=XYZ((i-1)*5+1,:)-mean(XYZ((i-1)*5+(1:5),:));
    V2=XYZ((i-1)*5+2,:)-mean(XYZ((i-1)*5+(1:5),:))-sin(pi/2-2*pi/5).*V1;
    V2=V2./norm(V2).*norm(V1);
    V5=S5_V(:,1).*V1+S5_V(:,2).*V2+mean(XYZ((i-1)*5+(1:5),:));
    V5=V5./vecnorm(V5')'.*(1+sin(1-vecnorm(V5')')./4);
    patch('Faces',S5_F,'Vertices',V5,'FaceColor',[1,1,1].*.2,'EdgeColor','none');
end
light
material dull

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/36246.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

判断一个时间段是否经过了另一个时间段

判断一个时间段是否经过了另一个时间段

场景&#xff1a; IOT设备存在离线与恢复时间记录&#xff0c;每一次离线和恢复记为一个周期即一条数据, 现在需要统计出在某个时段存在离线记录的数据,如果目前未恢复,没有恢复时间&#xff0c;恢复时间置为9999-01-01 00:00:00 原始数据如下(t_offline_record)&#xff1a;…
阅读更多...
OPengl学习——初识opengl

OPengl学习——初识opengl

文章目录1、网站罗列2、一些词语解析1.入门概念2.Opengl Vs DirectX3、QOpenGLWidget4、引用**OpenGL&#xff08;Open Graphics Library&#xff09;*是一个跨编程语言、跨平台的编程图形程序接口&#xff0c;它将计算机的资源抽象称为一个个OpenGL的对象&#xff0c;对这些资…
阅读更多...
3.5、点对点协议 PPP

3.5、点对点协议 PPP

3.5、点对点协议 PPP 3.5.1、基本介绍 点对点协议 PPP(Point-to-Point Protocol) 是目前使用最广泛的点对点数据链路层协议。 用户计算机只有获取到 ISP 所分配的合法 IP 地址后&#xff0c;才能成为因特网上的主机 用户计算机与 ISP 进行通信时&#xff0c;所使用的数据链路…
阅读更多...
【学习笔记21】JavaScript数组的基本方法

【学习笔记21】JavaScript数组的基本方法

笔记首发 一、push&#xff1a;末位新增 语法: 数组.push(数据)作用: 向数组末尾添加数据返回值: 追加数据后, 数组最新的长度 var arr [10, 20, 30, 40];console.log(原始数组: , arr); ​var num arr.push(500);console.log(push新增后数组: , arr);console.log(push的返回…
阅读更多...
进程的初识

进程的初识

目录预备知识 -> 操作系统操作系统的定义操作系统的定位进程进程的概念进程调度的过程进程的管理描述组织PCB描述进程的特征进程调度的相关属性进程的状态优先级上下文记账信息预备知识 -> 操作系统 操作系统的定义 操作系统是一个搞管理的软件 对上&#xff0c;要对硬…
阅读更多...
为什么一定要申请专利呢

为什么一定要申请专利呢

问题一&#xff1a;如何避免被判为非正常专利&#xff1f; 原本有个发明创造&#xff0c;想申请专利&#xff0c;却被列入非正常申请&#xff0c;甚至违法。以下五种情况一定要注意&#xff0c;千万不能碰。 1、同一单位或个人申请多件明显抄袭现有技术的专利&#xff1b; 2…
阅读更多...
如何通过 Java 合并和取消合并 Excel 单元格

如何通过 Java 合并和取消合并 Excel 单元格

在整理 Excel 中的数据时&#xff0c;我们不可避免地需要合并和取消合并单元格。同时&#xff0c;如果需要创建跨列或行的标题&#xff0c;我们可以合并 Excel 单元格以在电子表格中轻松完成此操作。 合并单元格是指将两个或多个单元格合并为一个单元格&#xff0c;而取消合并单…
阅读更多...
4.4——数据库和前后端身份认证

4.4——数据库和前后端身份认证

目录数据库与身份认证数据库的基本概念什么是数据库常见的数据库及分类传统型数据库的数据组织结构安装并配置 MySQL使用 MySQL Workbench 管理数据库连接数据库了解主界面的组成部分创建数据库创建数据表向表中写入数据使用 SQL 管理数据库在项目中操作 MySQL安装与配置 mysql…
阅读更多...
华为机试 - 数大雁

华为机试 - 数大雁

目录 题目描述 输入描述 输出描述 用例 题目解析 算法源码 题目描述 一群大雁往南飞&#xff0c;给定一个字符串记录地面上的游客听到的大雁叫声&#xff0c;请给出叫声最少由几只大雁发出。 具体的: 1.大雁发出的完整叫声为”quack“&#xff0c;因为有多只大雁同一时…
阅读更多...
怎么还不会进制转换，进来学。

怎么还不会进制转换，进来学。

✨进制转换&#xff0c;深度讲解✨特殊的十进制转换&#xff08;整数&#xff09;一、十进制转换为其他进制二、其他进制转换为十进制二进制的特殊转换&#xff08;整数&#xff09;一、二进制转换为其他进制二、其他进制转换为二进制任意进制的转换&#xff08;整数&#xff0…
阅读更多...
Java项目：JSP高校新生报到迎新管理系统

Java项目：JSP高校新生报到迎新管理系统

作者主页&#xff1a;源码空间站2022 简介&#xff1a;Java领域优质创作者、Java项目、学习资料、技术互助 文末获取源码 项目介绍 辅导员角色包含以下功能&#xff1a; 辅导员登录,学生留言管理,新生报到管理,宿舍分配管理等功能。 财务管理角色包含以下功能&#xff1a; 财务…
阅读更多...
一道Android题目逆向动态调试

一道Android题目逆向动态调试

题目来源于海淀区网络与信息安全管理员大赛&#xff0c;题目中将加密验证算法打包进.so&#xff0c;在程序中动态调用check。 本题目通过System.loadLibrary(“native-lib”)加载了libnative-lib.so文件&#xff0c;该文件通过jeb可以实现提取 图1 题目关键代码 调试环境选择…
阅读更多...
【矩阵论】4.矩阵运算——广义逆——定义性质与特殊矩阵的广义逆

【矩阵论】4.矩阵运算——广义逆——定义性质与特殊矩阵的广义逆

4.3 广义逆 4.3.1 定义 若mn矩阵AAmn与矩阵XXnm满足四个条件①AXAA,②XAXX&#xff0c;③(AX)HAX,④(XA)HXA则X为A的加号逆(广义逆)&#xff0c;记为XA\begin{aligned} &若 m\times n 矩阵AA_{m\times n} 与矩阵 XX_{n\times m} 满足四个条件\\ &①AXAA,\quad ② XAXX…
阅读更多...
以太坊：轻松理解EIP-4844

以太坊：轻松理解EIP-4844

以太坊&#xff1a;轻松理解EIP-4844 以太坊网络在不断发展&#xff0c;多年来已经提出了许多技术提案。其中一个提案是由Vitalik Buterin提出的EIP-4844&#xff0c;它关注的是分片技术。 什么是EIP-4844&#xff0c;它将如何影响以太坊网络及其用户的未来&#xff1f;以下是…
阅读更多...
体系结构28_多处理机（2）

体系结构28_多处理机（2）

对称式共享存储器体系结构 多处理机Cache一致性 **多个处理器共享一个存储器 **当处理器规模较小时&#xff0c;这种机器十分经济 **支持对共享数据和私有数据的Cache缓存 私有数据供一个单独的处理器使用&#xff0c;而共享数据供多个处理器使用 ** 共享数据进入Cache产生了一…
阅读更多...
LeetCode 654.最大二叉树 617合并二叉树 700二叉搜索树中的搜索 98验证二叉搜索树

LeetCode 654.最大二叉树 617合并二叉树 700二叉搜索树中的搜索 98验证二叉搜索树

文章目录654最大二叉树c代码实现python 代码实现617合并二叉树c 代码实现python 代码实现700二叉搜索树中的搜索c代码实现python 代码实现98验证二叉搜索树c 代码实现python 代码实现654最大二叉树 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归…
阅读更多...
[附源码]java毕业设计在线购物商城

[附源码]java毕业设计在线购物商城

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
[附源码]java毕业设计疫情居家隔离服务系统

[附源码]java毕业设计疫情居家隔离服务系统

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
阿里云与信通院邀您参与云原生安全用户调研

阿里云与信通院邀您参与云原生安全用户调研

云原生安全建设已经成为企业云原生平台建设、应用云原生化改造进程中的必备项。在云原生的大势所趋下&#xff0c;云的分布式架构、容器化部署、边界消失等特点也带来了有别于传统硬件安全的模式&#xff1a;镜像漏洞、容器逃逸、租户隔离等安全问题威胁着企业的云原生平台和应…
阅读更多...
Unity动态创建Avatar骨骼映射

Unity动态创建Avatar骨骼映射

目录前言1 了解Avatar骨骼映射2 动态创建Avatar骨骼映射2.1 寻找相关APIAvatarBuilder.BuildHumanAvatarDeclarationParametersReturnsDescriptionHumanDescriptionDescriptionProperties2.2 创建Skeleton数据2.3 创建Human映射关系2.4 创建Avatar3 总结前言 为了让单个动画可…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023