4.3 广义逆
4.3.1 定义
若 m × n 矩 阵 A = A m × n 与 矩 阵 X = X n × m 满 足 四 个 条 件 ① A X A = A , ② X A X = X , ③ ( A X ) H = A X , ④ ( X A ) H = X A 则 X 为 A 的 加 号 逆 ( 广 义 逆 ) , 记 为 X = A + \begin{aligned} &若 m\times n 矩阵A=A_{m\times n} 与矩阵 X=X_{n\times m} 满足四个条件\\ &①AXA=A,\quad ② XAX=X,\quad ③(AX)^H=AX,\quad ④(XA)^H=XA\\ &则X为A的加号逆(广义逆),记为X=A^+ \end{aligned} 若m×n矩阵A=Am×n与矩阵X=Xn×m满足四个条件①AXA=A,②XAX=X,③(AX)H=AX,④(XA)H=XA则X为A的加号逆(广义逆),记为X=A+
a. 性质
-
A与X互为加号逆
-
A + A^{+} A+ 具有唯一性
证 明 : ( 反 证 法 ) 假 设 X , Y 都 满 足 四 个 条 件 , 有 A X A = A , X A X = X , ( A X ) H = A X , ( A Y ) H = A Y , A Y A = A , Y A Y = Y , ( A Y ) H = A Y , ( Y A ) H = Y A 有 X = X A X = A = A Y A ( 替 换 右 侧 X ) X A Y A X = X ( A Y ) H ( A X ) H = X [ ( A X ) ( A Y ) ] H = A X A = A X ( A Y ) H = X A Y = A Y A = A ( 消 去 左 侧 X ) X A Y A Y = ( X A ) H ( Y A ) H Y = [ ( Y A ) ( X A ) ] H A = ( Y A ) H Y = Y 故 可 得 A + 具 有 唯 一 性 \begin{aligned} &证明:(反证法)\\ &假设X,Y都满足四个条件,有AXA=A,XAX=X,(AX)^H=AX,(AY)^H=AY,\\ &AYA=A,YAY=Y,(AY)^H=AY,(YA)^H=YA\\ &有X=XAX\xlongequal{A=AYA(替换右侧X)}XAYAX=X(AY)^H(AX)^H=X[(AX)(AY)]^H\\ &\xlongequal{AXA=A}X(AY)^H=XAY\xlongequal{AYA=A(消去左侧X)}XAYAY=(XA)^H(YA)^HY=\\ &[(YA)(XA)]^HA=(YA)^HY=Y\\ &故可得A^+具有唯一性 \end{aligned} 证明:(反证法)假设X,Y都满足四个条件,有AXA=A,XAX=X,(AX)H=AX,(AY)H=AY,AYA=A,YAY=Y,(AY)H=AY,(YA)H=YA有X=XAXA=AYA(替换右侧X)XAYAX=X(AY)H(AX)H=X[(AX)(AY)]HAXA=AX(AY)H=XAYAYA=A(消去左侧X)XAYAY=(XA)H(YA)HY=[(YA)(XA)]HA=(YA)HY=Y故可得A+具有唯一性 -
A + A^+ A+ 的H穿脱公式: ( A H ) + = ( A + ) H (A^H)^+=(A^+)^H (AH)+=(A+)H
-
乘积的加号逆无穿脱公式: ( A B ) + ≠ B + A + (AB)^+\neq B^+A^+ (AB)+=B+A+
b. 广义逆特例
-
A = 0 A=0 A=0 ,则 A + = 0 A^{+}=0 A+=0
-
若方阵 A = A n × n A=A_{n\times n} A=An×n 可逆 ( ∣ A ∣ ≠ 0 \vert A \vert\neq 0 ∣A∣=0) ,则 A + = A − 1 A^+=A^{-1} A+=A−1
-
若 A = ( a ) A=(a) A=(a) 为1阶阵,即 A = ( 复 数 a ) A=(复数a) A=(复数a) ,则有 ( a ) + = a + = { a − 1 , a ≠ 0 0 , a = 0 (a)^+=a^+=\left\{\begin{aligned}a^{-1},&a\neq 0\\0,&a=0\end{aligned}\right. (a)+=a+={a−1,0,a=0a=0
-
对角阵 D = ( a 1 a 2 ⋱ a n ) D=\left(\begin{matrix}a_1&&&\\&a_2&&\\&&\ddots\\&&&a_n\end{matrix}\right) D=⎝⎜⎜⎛a1a2⋱an⎠⎟⎟⎞ ,则 D + = ( a 1 + a 2 + ⋱ a n + ) D^+=\left(\begin{matrix}a_1^+&&&\\&a_2^+&&\\&&\ddots\\&&&a_n^+\end{matrix}\right) D+=⎝⎜⎜⎛a1+a2+⋱an+⎠⎟⎟⎞
eg:
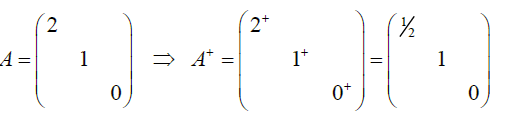
D + D = D D + D^+D=DD^+ D+D=DD+ ,且 ( D + ) k = ( D k ) + (D^+)^k=(D^k)^+ (D+)k=(Dk)+ ,(k=1,2,…)
证明:

-
A为Hermite幂等阵,即 A H = A = A 2 A^H=A=A^2 AH=A=A2 ,则 A + = A A^+=A A+=A
-
若A为列优阵( A H A = I A^HA=I AHA=I) ,则 A + = A H A^+=A^H A+=AH
证 明 : 由 于 A 是 列 半 U 阵 , 则 A H A = I A H A A H = A H , A A H A = A , ( A H A ) H = I = A H A , ( A A H ) H = A A H \begin{aligned} &证明:由于 A 是列半U阵,则 A^HA=I\\ &A^HAA^H=A^H,AA^HA=A,(A^HA)^H=I=A^HA,(AA^H)^H=AA^H \end{aligned} 证明:由于A是列半U阵,则AHA=IAHAAH=AH,AAHA=A,(AHA)H=I=AHA,(AAH)H=AAH若 A H A^H AH 为列优阵(A为行优阵)( A A H = I AA^H=I AAH=I) ,则 A + = A H A^+=A^H A+=AH
证 明 : 由 于 A 是 行 半 U 阵 , 则 A A H = I A H A A H = A H , A A H A = A , ( A H A ) H = A H A , ( A A H ) H = I = A A H \begin{aligned} &证明:由于 A 是行半U阵,则 AA^H=I\\ &A^HAA^H=A^H,AA^HA=A,(A^HA)^H=A^HA,(AA^H)^H=I=AA^H \end{aligned} 证明:由于A是行半U阵,则AAH=IAHAAH=AH,AAHA=A,(AHA)H=AHA,(AAH)H=I=AAH
-
若A为U阵(
单位正交阵),则 A + = A H = A − 1 A^+=A^H=A^{-1} A+=AH=A−1若A为U阵,则 A H A = A A H = I , A H = A − 1 A^HA=AA^H=I,A^H=A^{-1} AHA=AAH=I,AH=A−1
A H A A H = A H , A A H A = A , ( A A H ) H = I = A A H , ( A H A ) H = A H A A^HAA^H=A^H,AA^HA=A,(AA^H)^H=I=AA^H,(A^HA)^H=A^HA AHAAH=AH,AAHA=A,(AAH)H=I=AAH,(AHA)H=AHA ,故 A + = A H A^+=A^H A+=AH
-
若A为单阵(
可相似对角化)且可逆 ,则有谱分解 A = λ 1 G 1 + ⋯ + λ k G k A=\lambda_1G_1+\cdots+\lambda_kG_k A=λ1G1+⋯+λkGk 且 A + = λ 1 − 1 G 1 + ⋯ + λ k − 1 G k A^+=\lambda_1^{-1}G_1+\cdots+\lambda_k^{-1}G_k A+=λ1−1G1+⋯+λk−1Gk若不满足可逆条件,则未必成立
-
若A为正规阵(
正规方阵),则 A + A^+ A+ 也为正规阵有正规分解 A = Q D D H A=QDD^H A=QDDH ,则 A + = Q D + Q H A^+=QD^+Q^H A+=QD+QH
有谱分解 A = λ 1 + G 1 + ⋯ + λ k + G k A=\lambda_1^+G_1+\cdots+\lambda_k^{+}G_k A=λ1+G1+⋯+λk+Gk
c. A A + AA^+ AA+ 与 A + A A^+A A+A 相关结论
-
A A + AA^+ AA+ 与 A + A A^+A A+A 都是Hermite阵
-
r ( A + A ) = r ( A A + ) = r ( A ) r(A^+A)=r(AA^+)=r(A) r(A+A)=r(AA+)=r(A)
由于矩阵的秩越乘越小,则 r ( A A + ) ≤ r ( A ) r(AA^+)\le r(A) r(AA+)≤r(A) 而 A = A A + A A=AA^+A A=AA+A ,则 r ( A ) ≤ r ( A A + ) r(A)\le r(AA^+) r(A)≤r(AA+) ,故有 r ( A A + ) ≤ r ( A ) ≤ r ( A A + ) r(AA^+)\le r(A)\le r(AA^+) r(AA+)≤r(A)≤r(AA+)
-
幂等性: ( A A + ) 2 = A A + (AA^+)^2=AA^+ (AA+)2=AA+ , ( A + A ) 2 = A + A (A^+A)^2=A^+A (A+A)2=A+A
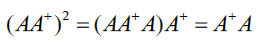
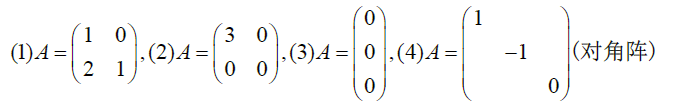
( 1 ) A = ( 1 0 2 1 ) 为 可 逆 阵 , 则 A + = A − 1 = ( 1 0 − 2 1 ) , A = ( a b c d ) = 1 ∣ A ∣ ( d − b − c a ) ( 2 ) ( 3 ) ( 4 ) 中 A 为 对 角 阵 \begin{aligned} &(1)A=\left( \begin{matrix}1&0\\2&1 \end{matrix} \right)为可逆阵,则A^+=A^{-1}=\left( \begin{matrix}1&0\\-2&1 \end{matrix} \right),A=\left( \begin{matrix} a&b\\c&d \end{matrix} \right)=\frac{1}{\vert A\vert}\left( \begin{matrix} d&-b\\-c&a \end{matrix} \right)\\ &(2)(3)(4)中A为对角阵 \end{aligned} (1)A=(1201)为可逆阵,则A+=A−1=(1−201),A=(acbd)=∣A∣1(d−c−ba)(2)(3)(4)中A为对角阵
-
λ ( A A + ) 与 λ ( A + A ) \lambda(AA^+) 与 \lambda(A^+A) λ(AA+)与λ(A+A) 都有r(A) 个1
设 A ∈ C m , n , A + ∈ C n , m A\in C^{m,n},A^+\in C^{n,m} A∈Cm,n,A+∈Cn,m 由于 A A + AA^+ AA+ 与 A + A A^+A A+A 都是 Hermite 阵,且 A + A A^+A A+A 是幂等阵, ( A A + ) 2 = A A + , ( A + A ) 2 = A + A (AA^+)^2=AA^+,(A^+A)^2=A^+A (AA+)2=AA+,(A+A)2=A+A ,由Caley定理 x 2 = x x^2=x x2=x 则其0化式为 x 2 − x = 0 x^2-x=0 x2−x=0 , A A + AA^+ AA+ 有两个不同的根1和0
已知 r ( A + A ) = r ( A A + ) = r ( A ) = r r(A^+A)=r(AA^+)=r(A)=r r(A+A)=r(AA+)=r(A)=r ,
则 A A + AA^+ AA+ 有r个正根,m-r 个0根; A + A A^+A A+A 有r个正根,n-r 个0根
-
A + A A^+A A+A 与 A A + AA^+ AA+ 都是半正定阵 ( A A + ≥ 0 , A + A ≥ 0 AA^+ \ge 0,A^+A\ge 0 AA+≥0,A+A≥0)
已知 A + A A^+A A+A 为幂等阵,则 ( A A + ) 2 = ( A A + ) H ( A A + ) = P = A A + P H P ≥ 0 (AA^+)^2=(AA^+)^H(AA^+)\xlongequal{P=AA^+}P^HP\ge 0 (AA+)2=(AA+)H(AA+)P=AA+PHP≥0 ,故 A A + AA^+ AA+ 为半正定阵,同理 A A + AA+ AA+ 为半正定阵
由Caley定理, x 2 = x x^2=x x2=x ,则0化式 x ( x − 1 ) = 0 x(x-1)=0 x(x−1)=0 ,故特根 ≥ \ge ≥ 0 ,为半正定阵
-
一般有 A A + ≠ I AA^+\neq I AA+=I , A + A ≠ I A^+A\neq I A+A=I , 且 A A + ≠ A + A AA^+\neq A^+A AA+=A+A
-
若 A 为正规阵,则 A + A = A A + A^+A=AA^+ A+A=AA+ ,且 ( A + ) k = ( A k ) + , k = 0 , 1 , 2 , ⋯ (A^+)^k=(A^k)^+,k=0,1,2,\cdots (A+)k=(Ak)+,k=0,1,2,⋯
由 于 A 是 正 规 阵 , 则 A A H = A H A , A 有 正 规 分 解 A = Q D Q H = Q ( λ 1 ⋱ λ n ) Q H , 其 中 Q 为 U 阵 ⇒ A + = ( Q D Q H ) + = ( Q H ) + D + Q + = Q + = Q H Q D + Q H , ⇒ ( A + ) k = ( Q D + Q H ) k = Q ( D + ) k Q H = Q ( D k ) + Q H = ( A k ) + 且 A + A = ( Q D + Q H ) Q D Q H = ( Q D + D Q H ) = Q D D + Q H = ( Q D Q H ) ( Q D + Q H ) = A A + \begin{aligned} &由于A是正规阵,则AA^H=A^HA,A有正规分解A=QDQ^H=Q\left( \begin{matrix} \lambda_1&&\\&\ddots&\\&&\lambda_n \end{matrix} \right)Q^H,\\ &其中Q为U阵 \\ &\Rightarrow A^+=(QDQ^H)^+=(Q^H)^+D^+Q^+\xlongequal{Q^+=Q^H}QD^+Q^H,\\ &\Rightarrow (A^+)^k=(QD^+Q^H)^k=Q(D^+)^kQ^H=Q(D^k)^+Q^H=(A^k)^+\\ &且A^+A=(QD^+Q^H)QDQ^H=(QD^+DQ^H)=QDD^+Q^H=(QDQ^H)(QD^+Q^H)=AA^+ \end{aligned} 由于A是正规阵,则AAH=AHA,A有正规分解A=QDQH=Q⎝⎛λ1⋱λn⎠⎞QH,其中Q为U阵⇒A+=(QDQH)+=(QH)+D+Q+Q+=QHQD+QH,⇒(A+)k=(QD+QH)k=Q(D+)kQH=Q(Dk)+QH=(Ak)+且A+A=(QD+QH)QDQH=(QD+DQH)=QDD+QH=(QDQH)(QD+QH)=AA+


![[附源码]java毕业设计在线购物商城](https://img-blog.csdnimg.cn/afe14e390e164eceb492753164b5686a.png)
![[附源码]java毕业设计疫情居家隔离服务系统](https://img-blog.csdnimg.cn/6199f314ed3a4856939c218c75be32b3.png)






![[附源码]java毕业设计婴幼儿玩具共享租售平台](https://img-blog.csdnimg.cn/09e8855f61824c6caa761e5b5e3ecedb.png)