C++不知算法系列之高精度数值处理算法

news2025/7/19 2:41:16

1. 前言

什么是高精度数值处理算法？

高精度数值指因受限于计算机硬件的制约，超过计算机所能存储范围的数值。既然不能存储，更谈不上运算。

对此类数值的加、减、乘、除运算需要提供针对性的算法方能获取到结果。此类算法的设计思路因有别于其它算法，为了研究的方便，称此类算法为高精度数值处理算法。

本文将讲解如何实现对此类数值的加、减、乘、除运算。

2. 高精度数值的运算

对高精度数值运算时，需要从 2 个方面入手：

  • 如何存储：其基本存储思想是把数值以字符串的形式输入，然后转储于整型类型的数组中。理论上，数组的长度是不受限制的，或者采用一部分一部分的处理方式。
  • 如何计算：基本计算思想是把计算的2个数值以数组形式存储后，以逐位逐位地方式进行计算。如此，把大问题化解成了小问题。

2.1 高精度的加法

高精度数值相加的思路：

  • 用整型数组存储 2 个加数。为了遵循数组从头指针向尾指针扫描的使用习惯，存储时，可以把低位存储在前面，高位存储存在后面，至于是否如此存储可以根据实际设计的算法决定。如下存储 374和65。
//加数一
int num1[100]={4,7,3,0,0……};
//加数二
int num2[100]={5,6,0,0……};
//相加结果,初始化为 0
int result[100]={0};
//存储两数相加的进位
int jinWei=0;
  • 遍历数组，对 2 个数组的对应位进行相加。如num1[0]+num2[0]，且把相加结果存储到 result[0]位置。相加时，需要根据加法运算法则，考虑进位和不进位两种情况。

不进位情况：如 num1[0]+num2[0]=4+5不需要进位，直接把结果存储到 result[0]中。

1.png

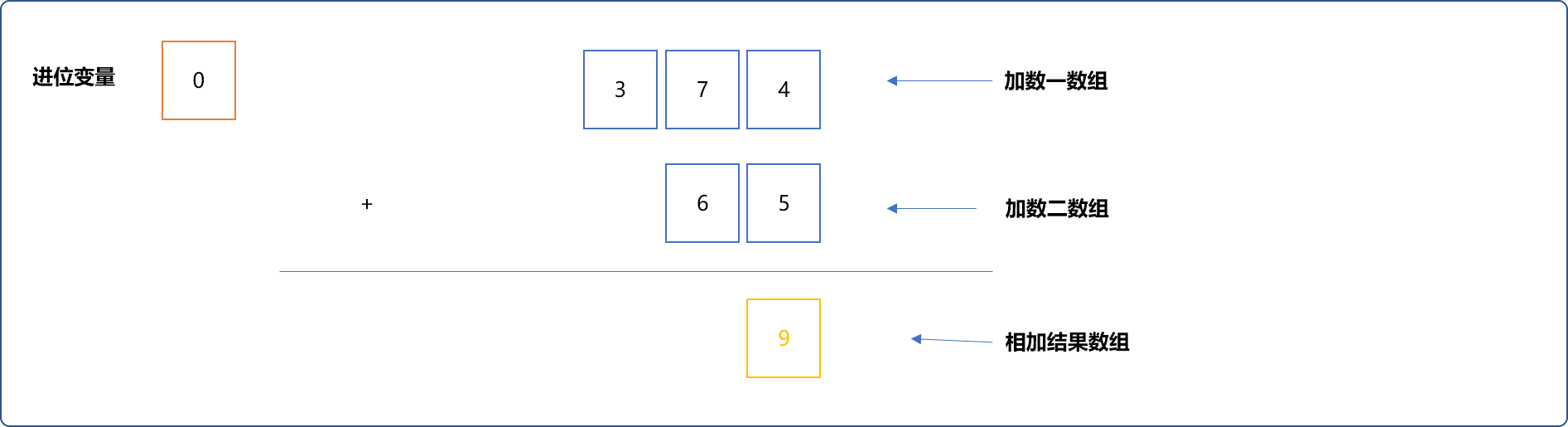
进位情况：如num1[1]+num2[1]=7+6=13。有进位操作，则把结果的余数存储在result[1]=3中。把结果的商（进位值）临时存储在变量jinWei中。

2.png

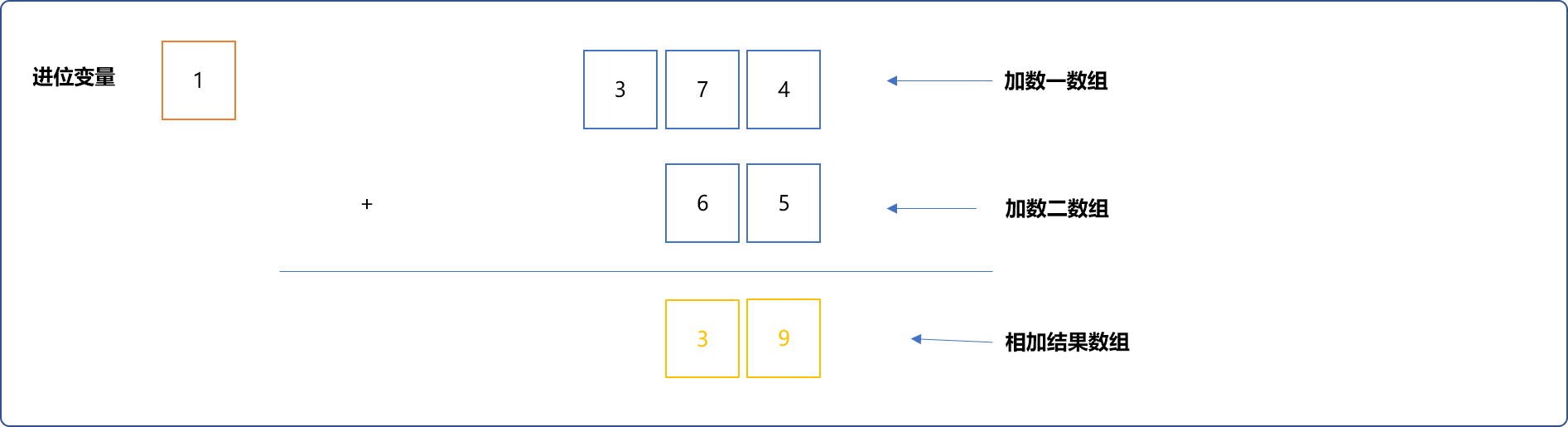
最后，num1[2]+num2[2]+jinWei=3+0+1=4存储在result[2]中。

3.png

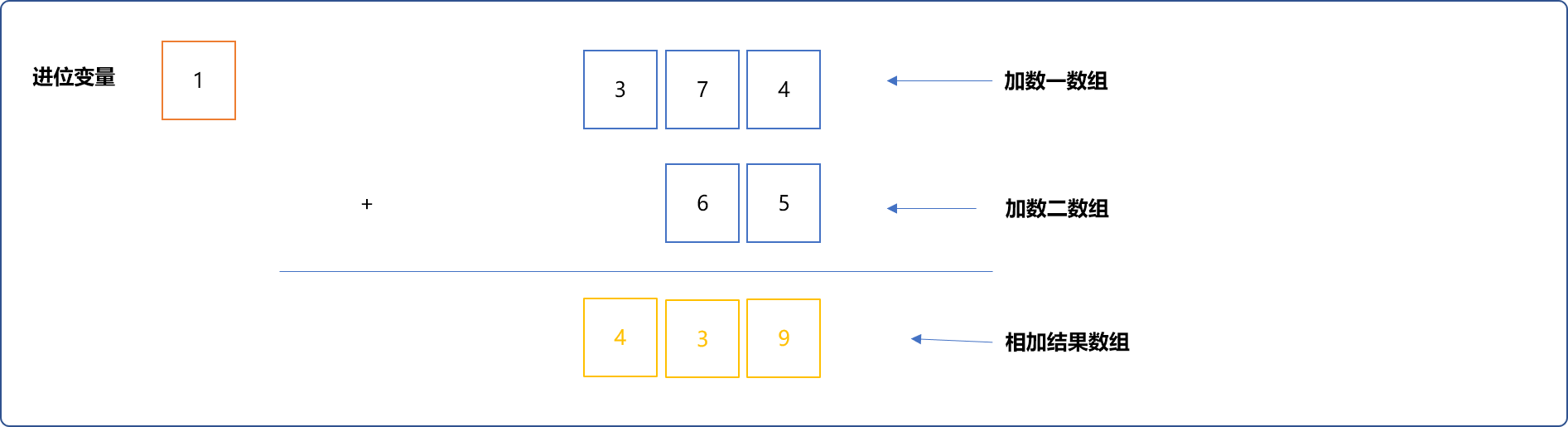
通用逻辑：

加数一和加数二对应位中的值和进位变量中的值一起相加，结果的余数存储在结果数组中，商存储在进位变量中。

编码实现：

#include <iostream>
#include <cstring>
using namespace std;
int main(int argc, char** argv) {
	//存储加数一(被加数),初始为 0
	int num1[100]= {0};
	//加数一的长度
	int numLen1=0;
	//存储加数二（加数），初始为 0
	int num2[100]= {0};
	//加数二的长度
	int numLen2=0;
	//存储结果
	int result[100]= {0};
	//存储进位值
	int jinWei=0;
	//加数一的字符串格式
	string numStr1;
	//加数二的字符串格式
	string numStr2;
	//输入加数一
	cout<<"请输入加数一："<<endl;
	cin>>numStr1;
	//转存至数组中(低位存储在数组的前面)
	numLen1= numStr1.size();
	for(int i=0; i<numLen1 ; i++) {
		num1[i]=numStr1[numLen1-1-i]-'0';
	}
	//输入加数二
	cout<<"请输入加数二："<<endl;
	cin>>numStr2;
	numLen2=numStr2.size();
	//转存至数组中(反序存储)
	for(int i=0; i<numLen2; i++) {
		num2[i]=numStr2[numLen2-1-i]-'0';
	}
	numLen1=numLen1>=numLen2?numLen1:numLen2;
	int idx=0;
	while(idx<numLen1) {
		//对应位相加，注意，要加上进位值
		result[idx]=num1[idx]+num2[idx]+jinWei;
		//存储进位数值
		jinWei=result[idx] / 10;
		//存储余数
		result[idx] %=10;
		idx++;
	}
    //处理进位值
	if(jinWei>0) {
		result[idx]=jinWei;
	} else {
		idx--;
	}
    //输出
	for(int i=idx; i>=0; i--) {
		cout<<result[i]<<"";
	}
	cout<<endl;
	return 0;
}

输出结果：

23.png

2.2 高精度的减法

减法是加法的逆操作，加法时需要考虑进位操作， 减法时则需要考虑借位与不借位两种情况。

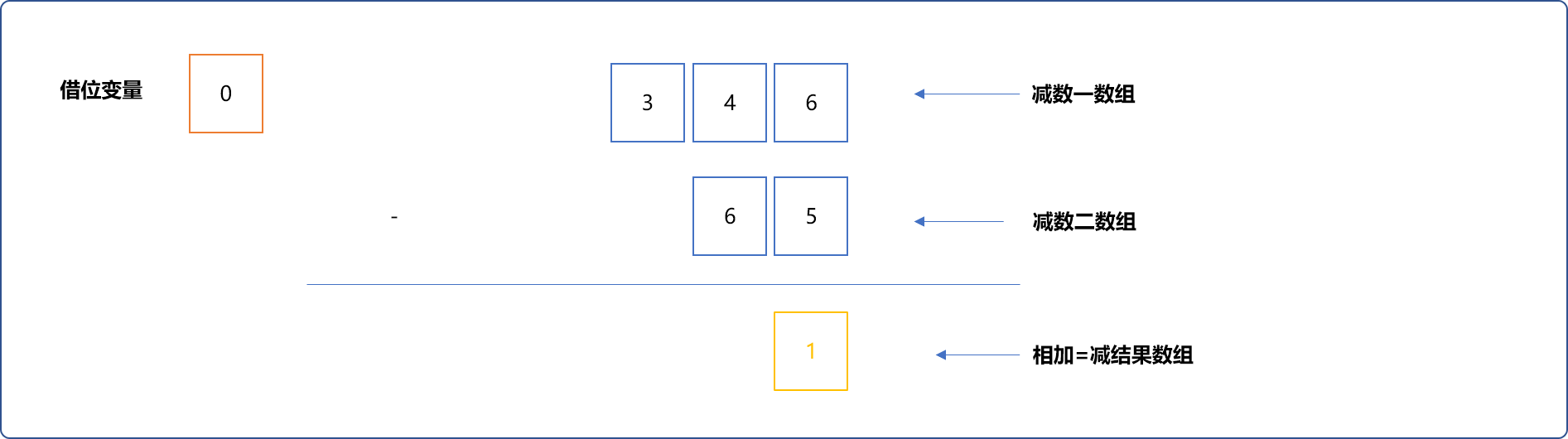
  • 不借位：6-5不需要借位。

4.png

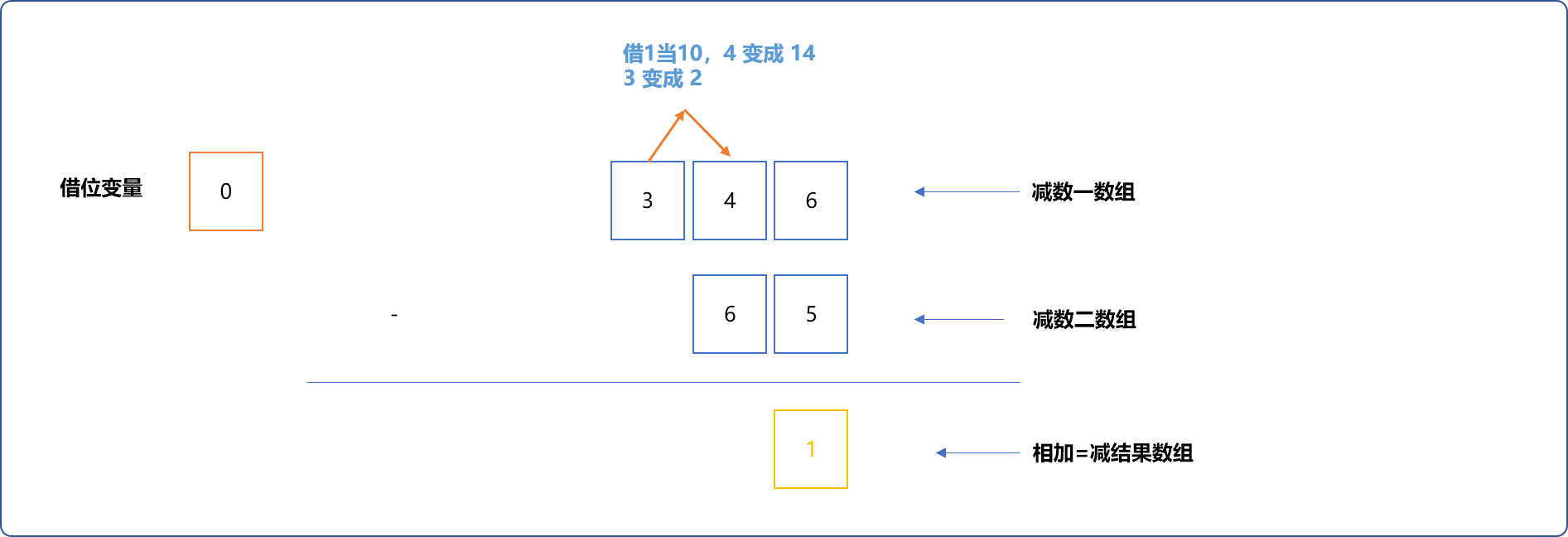
  • 借位：如下十位的 4减6，需要借位。向百位借 1 当10，4变成14。高位3变成2。

5.png

6.png

7.png

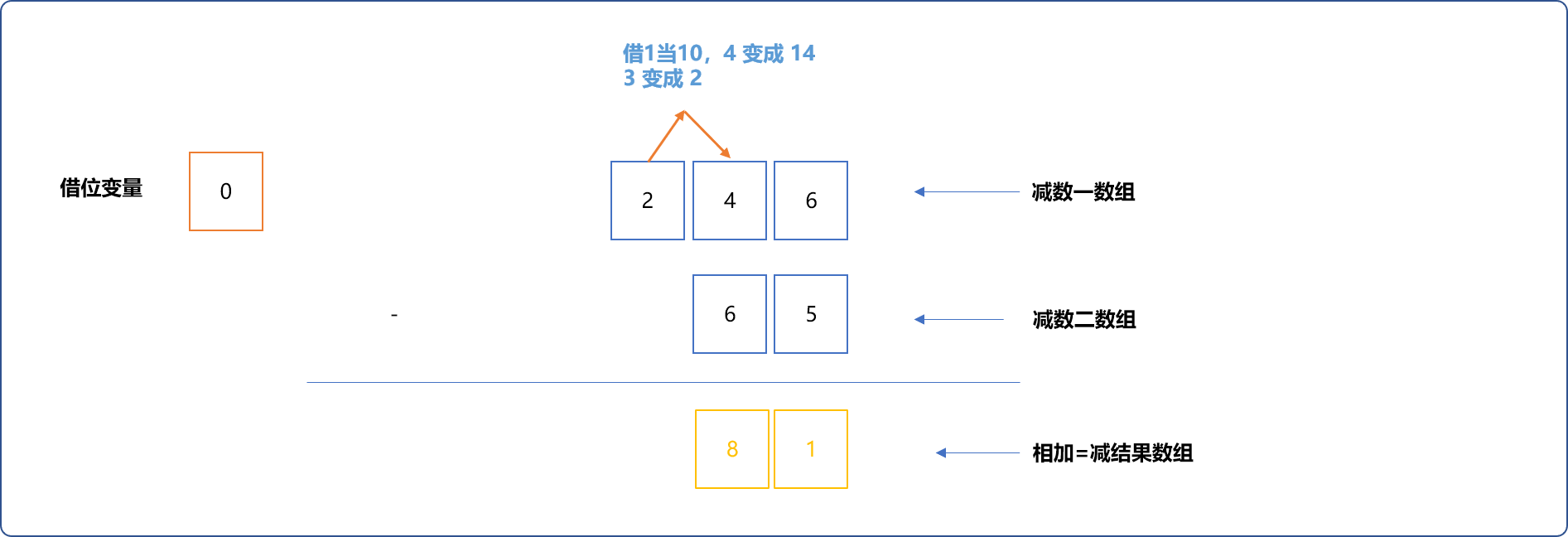
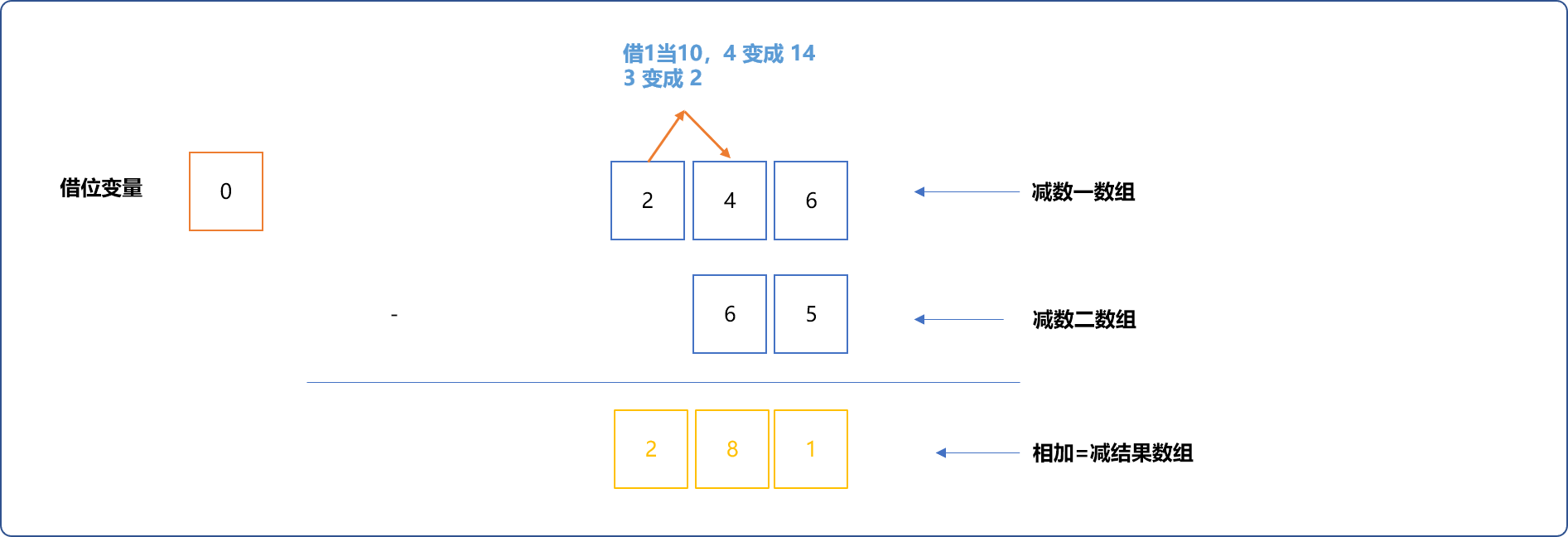
编码实现：

#include <iostream>
#include <cstring>
using namespace std;
int main(int argc, char** argv) {
	//存储减数一(被减数),初始为 0
	int num1[100]= {0};
	//减数一的长度
	int numLen1=0;
	//存储减数二（减数），初始为 0
	int num2[100]= {0};
	//减数二的长度
	int numLen2=0;
	//存储结果
	int result[100]= {0};
	//减数一的字符串格式
	string numStr1;
	//减数二的字符串格式
	string numStr2;
	//输入减数一
	cout<<"请输入减数一："<<endl;
	cin>>numStr1;
	//输入减数二
	cout<<"请输入减数二："<<endl;
	cin>>numStr2;
	//转存至数组中(反序存储)
	numLen1= numStr1.size();
	for(int i=0; i<numLen1 ; i++) {
		num1[i]=numStr1[numLen1-1-i]-'0';
	}
	numLen2=numStr2.size();
	//转存至数组中(反序存储)
	for(int i=0; i<numLen2; i++) {
		num2[i]=numStr2[numLen2-1-i]-'0';
	}
	numLen1=numLen1>=numLen2?numLen1:numLen2;
	int idx=0;
	while(idx<numLen1) {
		//是否需要借位
		if(num1[idx]<num2[idx]) {
			//需要借位
			num1[idx]+=10;
			num1[idx+1]--;
		}
		result[idx]=num1[idx]-num2[idx];
		idx++;
	}
	for(int i=idx; i>=0; i--) {
		if(result[i]!=0)
			cout<<result[i]<<"";
	}
	cout<<endl;
	return 0;
}

执行结果：

8.png

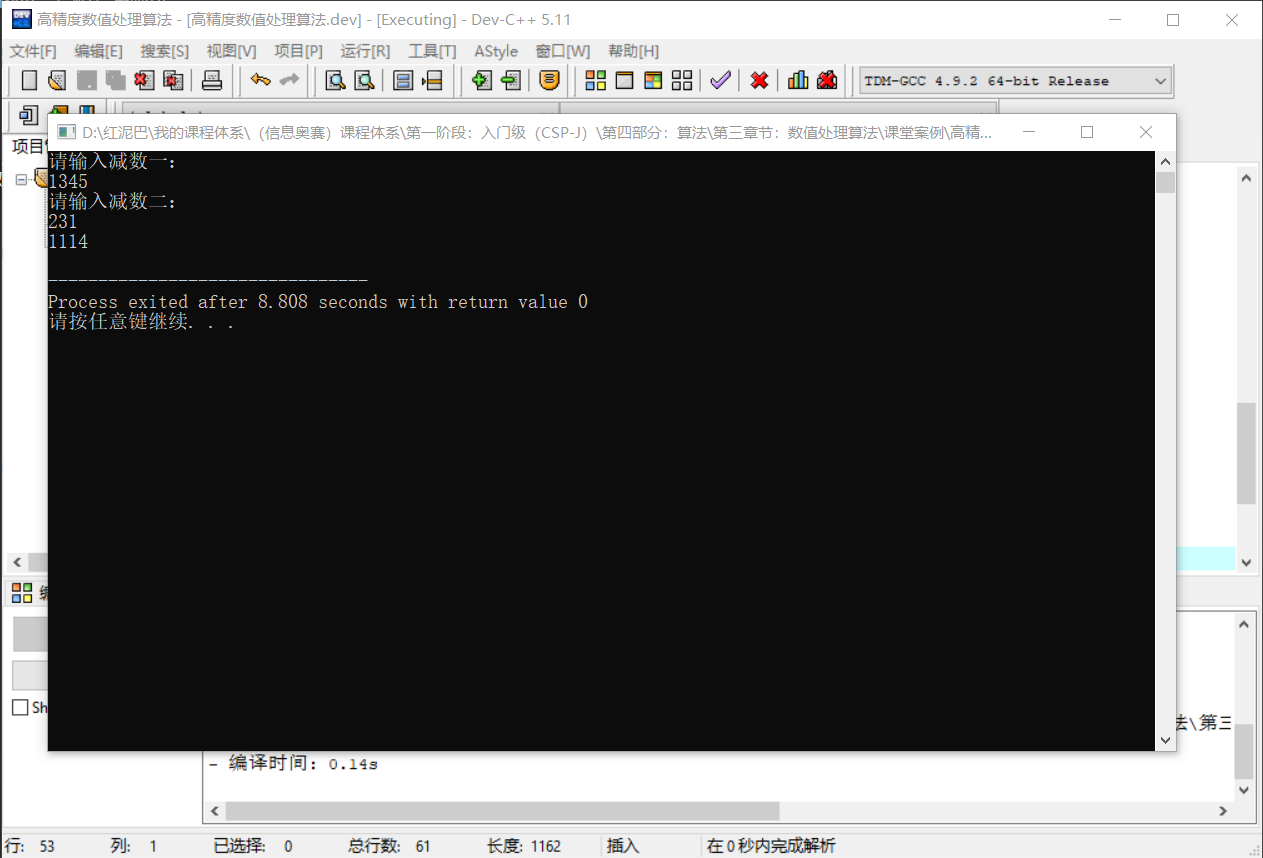
如上代码，对原数组中的数据会进行修改。

也可以如下实现：使用一个借位标志变量，用来标识对某位进行计算时，是否借过位。

#include <iostream>
#include <cstring>
using namespace std;
int mai123n(int argc, char** argv) {
    //省略……
    //是否借位标志信息
	int jieWei=0;
	int idx=0;
	while(idx<numLen1) {
		//如果被借位 
		if(jieWei==1) {
			//借位后是否小于减数 
			if(num1[idx]-jieWei<num2[idx]) {
				//需要再向高位借，借1 当 10 
				jieWei=1;
				result[idx]=num1[idx]-jieWei+jieWei*10-num2[idx];
			} else {
				//不需要借位 
				result[idx]=num1[idx]-jieWei-num2[idx];
				jieWei=0;
			}
		} else {
			//没有被借位 
			if(num1[idx]<num2[idx]) {
				//借 1 当 10 
				jieWei=1;
				result[idx]=num1[idx]+jieWei*10-num2[idx];
			} else {
				//不需要借位 
				jieWei=0;
				result[idx]=num1[idx]-num2[idx];
			}
		}
		idx++;
	}
    //省略……
	return 0;
}

虽然不会修改原数组中的数字，但逻辑有点累赘。

Tips：如上算法，需要保证大数减小数。

2. 3 高精度的乘法

商精度数值相乘可以有 2 种参考方案，如计算 246*65：

2.3.1 方案一

  • 把高精度被乘数246分别乘以乘数的每一位，如先乘以5得到1230，然后再把246乘以6得到1476。
  • 然后把1230和1476*10相加，得到15990。
  • 这种方案当乘数位数较多时，需要借用的临时存储空间会增多，且需要使用循环进行高精度数值累加。并不可取。

2.3.2 方案二

方案二和方案一同工异曲，不借助额外的空间存储数据，使用结果数组存储中间计算数值，也存储最终结果数值。不产生额外的空间使用代价。

在高精度乘法时，有一个位置关系需要了解。如nums1[100]={6,4,2}，nums[100]={5,6}，当使用result[100]存储最终相乘结果时，nums1[i]*nums2[j]的结果存储在 result[i+j]中。

**Tips：**从数学法则可知，当 2 数两乘时，百位乘以十位的值要存储在结果的千位上。

  • 先计算被乘数的个位数值 6乘以乘数 65 的结果，也就是计算 6*65的结果。这个其实很好计算，使用一个进位变量存储进位值。

9.png

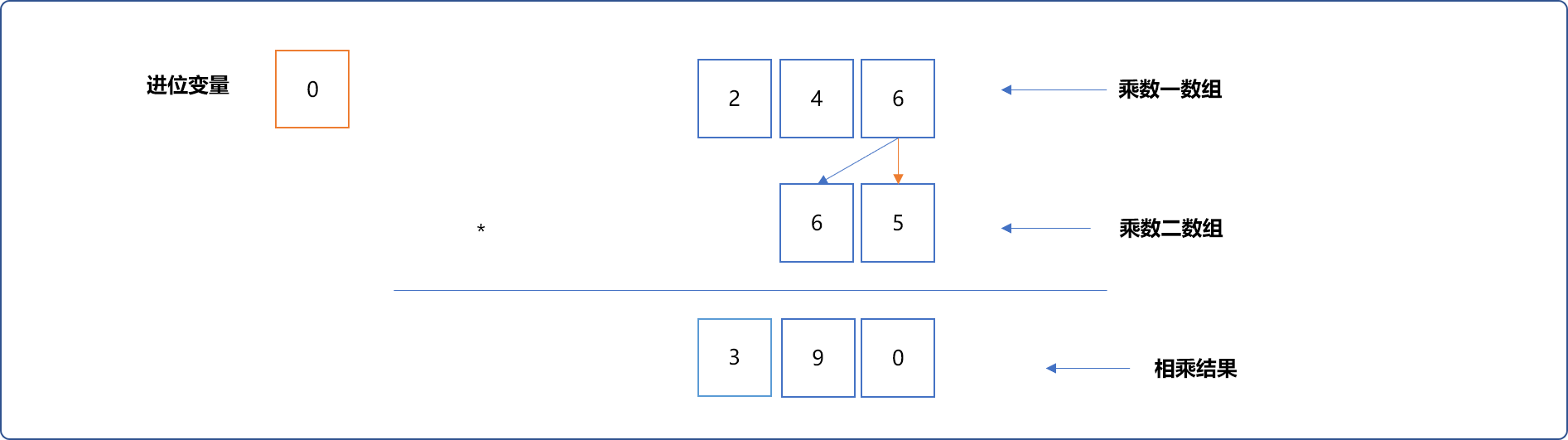
  • 再计算被乘数的十位数值 4乘以乘数的结果，也就计算机4*65的结果。在相乘时需要加上上述已经乘出来的结果 。如4*5+9=29。使用进位变量存储进位值，使用原来位置存储余数。

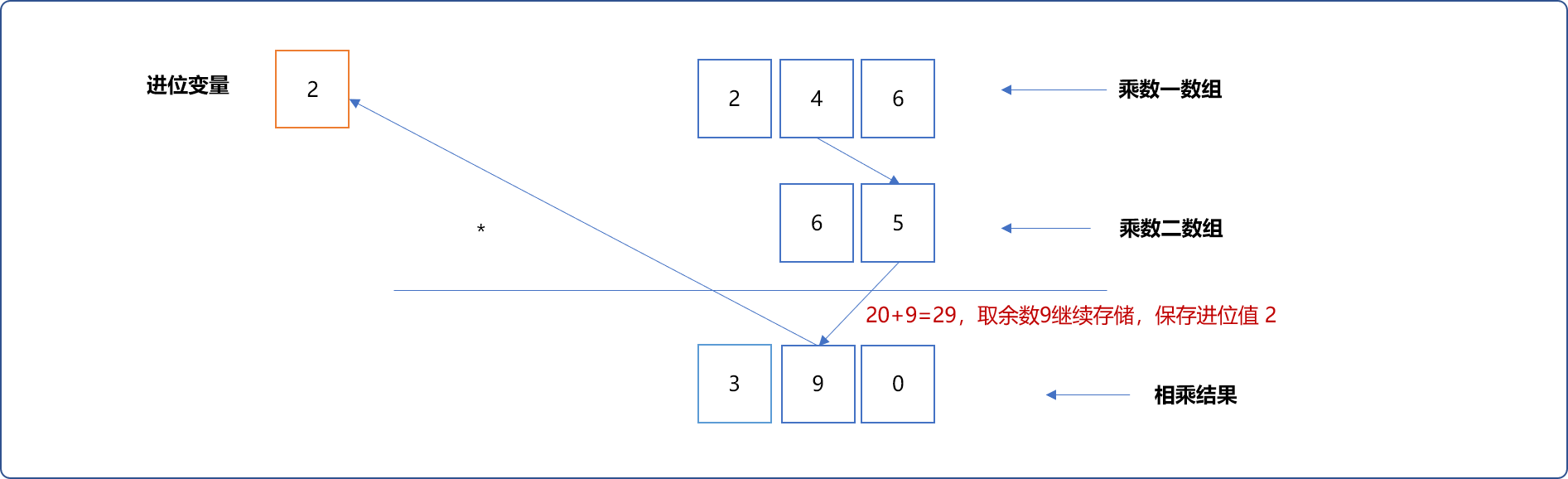
10.png

继续：4*6=24，加上原来的值3，再加上进位值2，最终结果是 29 ,取余数 9 存储，保存进位值 2。

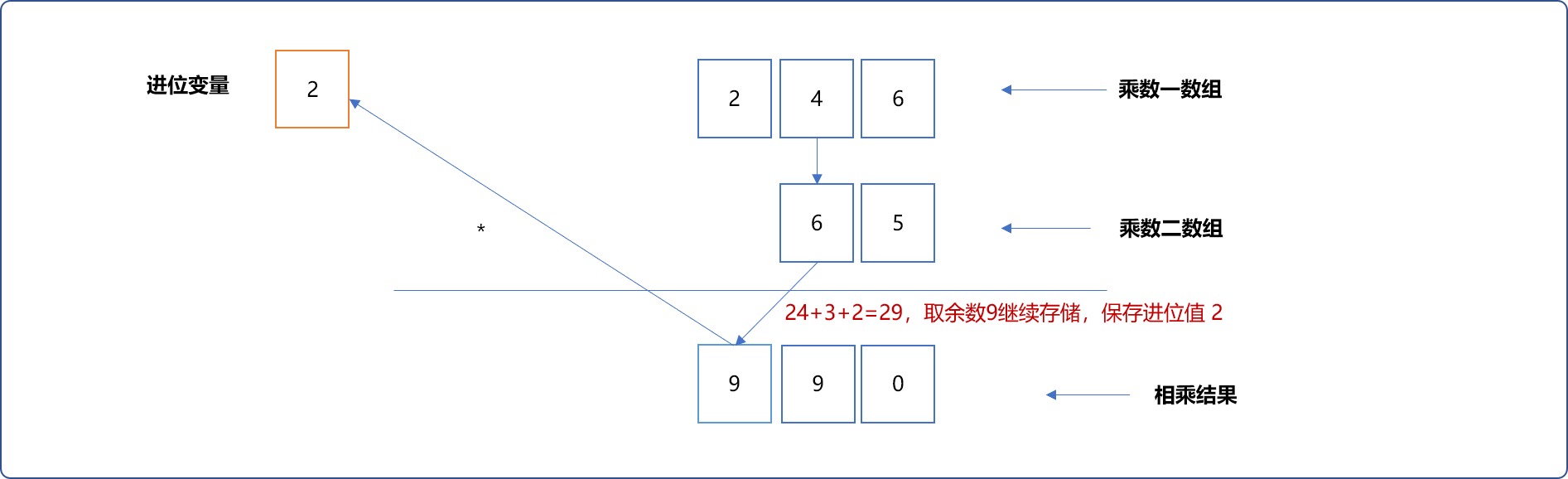
11.png

把最后的进位值作为进位作为结果数值存储 。

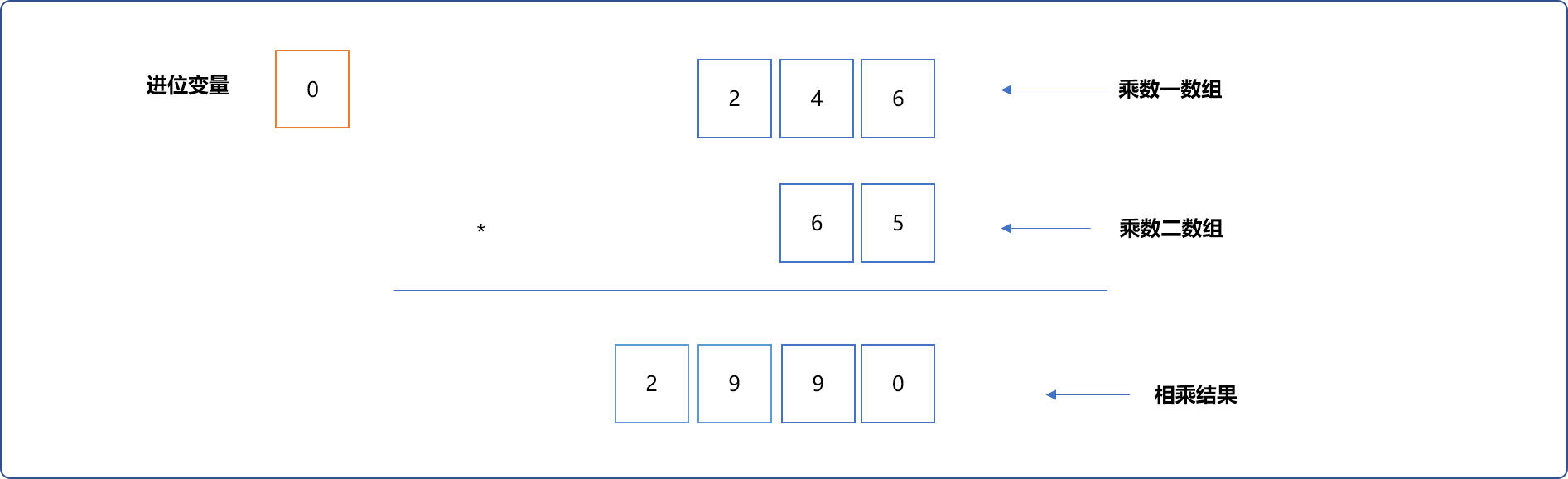
12.png

  • 把被乘数的百位2和乘数65相乘。逻辑和上面一样。

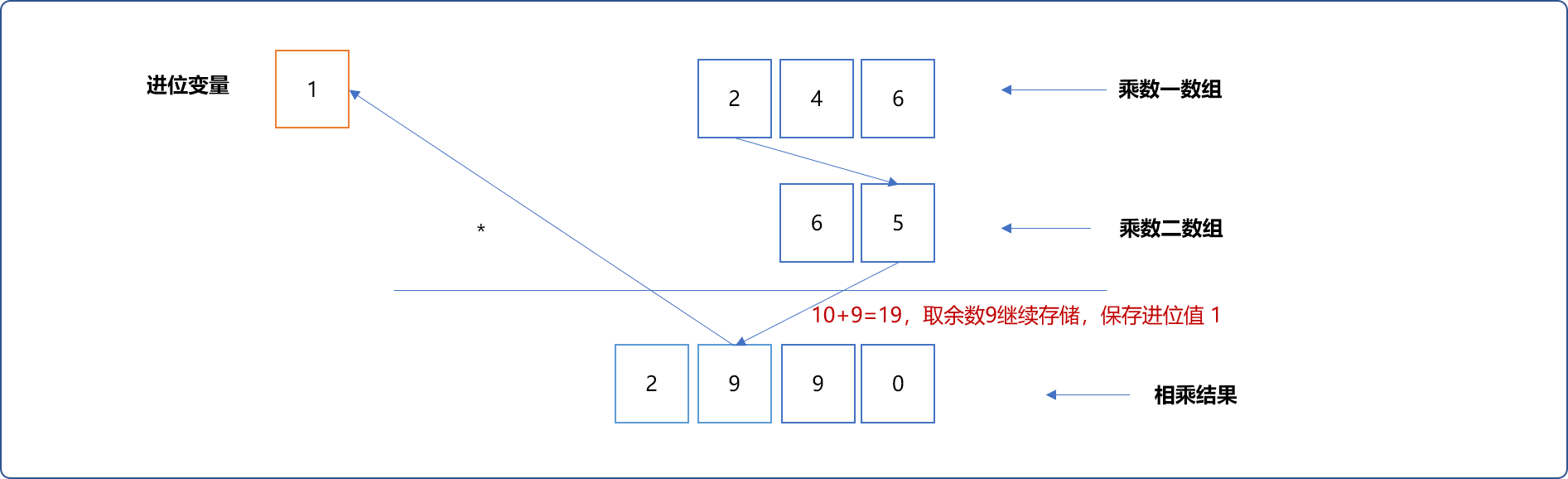
14.png

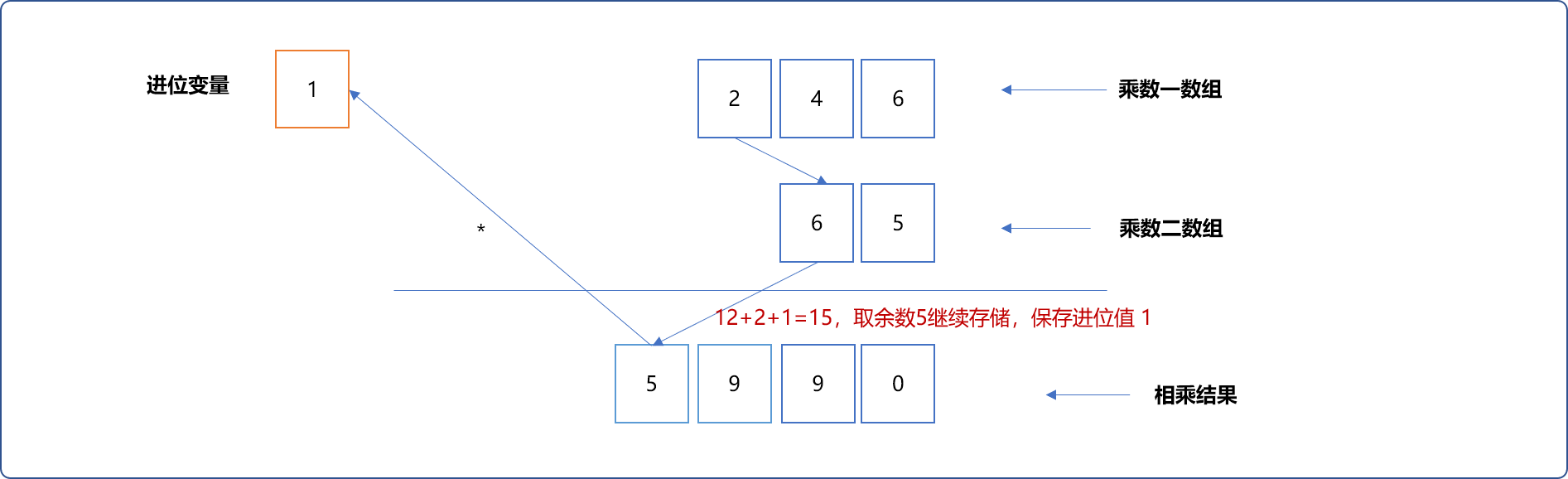
15.png

最后在结果中添加进位值。

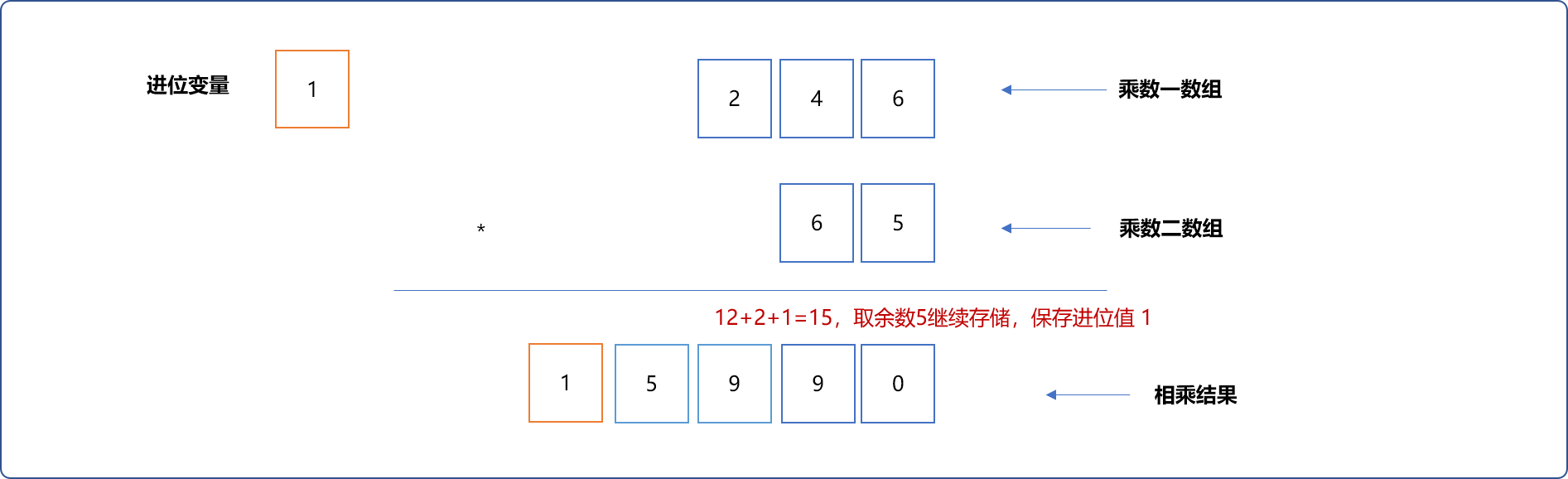
16.png

编程实现：

#include <iostream>
#include <cstring>
using namespace std;
int main(int argc, char** argv) {
    //省略乘数的输入，和前面相加数、相减数输入的代码一样
	for(int i=0; i<numLen1; i++) {
		int jinWei=0;
		for(int j=0; j<numLen2; j++) {
            //对应位相乘时需要加上原来的数值和进位值，可参照上面的演示图
			result[i+j]=num1[i]*num2[j]+jinWei+result[i+j];
			jinWei=result[i+j]/10;
			result[i+j]%=10;
		}
        //把进位值添加到结果数组中……
		result[i+numLen2]=jinWei;
	}
	int c=numLen1+numLen2;
	while(result[c]==0 && c>1)
		c--;
	for(int i=c; i>=0; i--) {
		cout<<result[i];
	}
	cout<<endl;
	return 0;
}

输出结果：

17.png

2.4 高精度相除

高精度相除分 2 种情况讨论：

  • 高精度除以低精度（低精度指计算机可以直接存储的数值）。
  • 高精度除以高精度。

2.4.2 高精度除以低精度

所谓高精度除以低精度，存储每次相除的商（0~9之间），其余数和被除数后面数字相加，作为新的被除数继续做除法。

如计算 642除以5的流程：

  • 6除以5。商为1作为结果，余数1暂存起来。

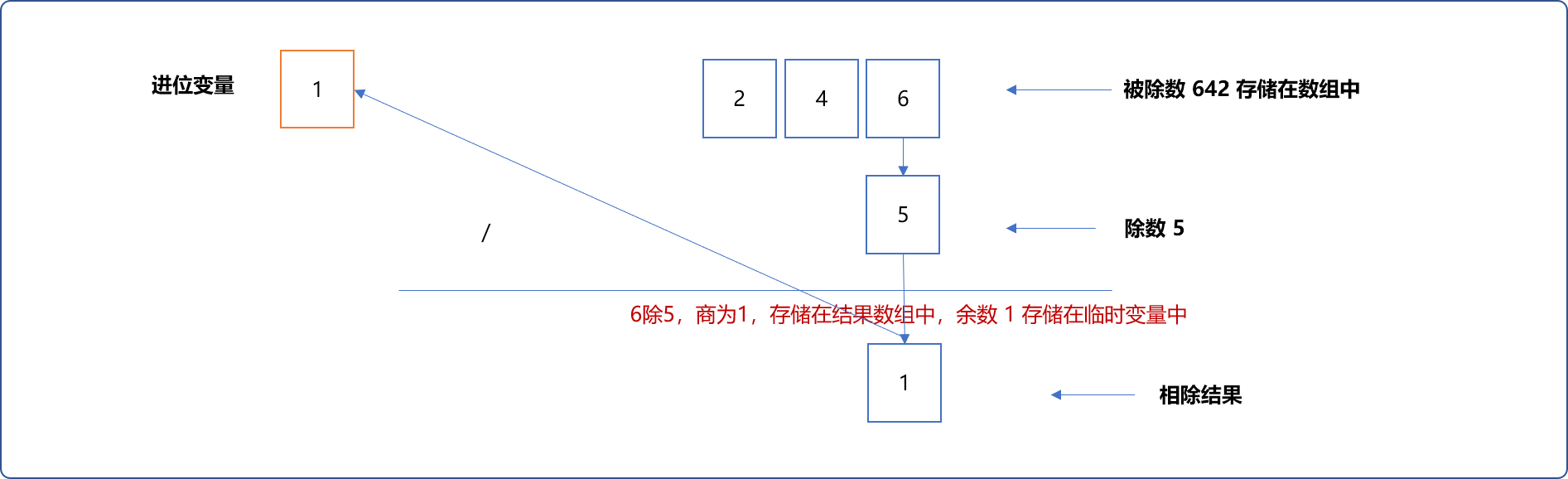
18.png

  • 4除5时，被除数需要加上上次余数的10倍再除。

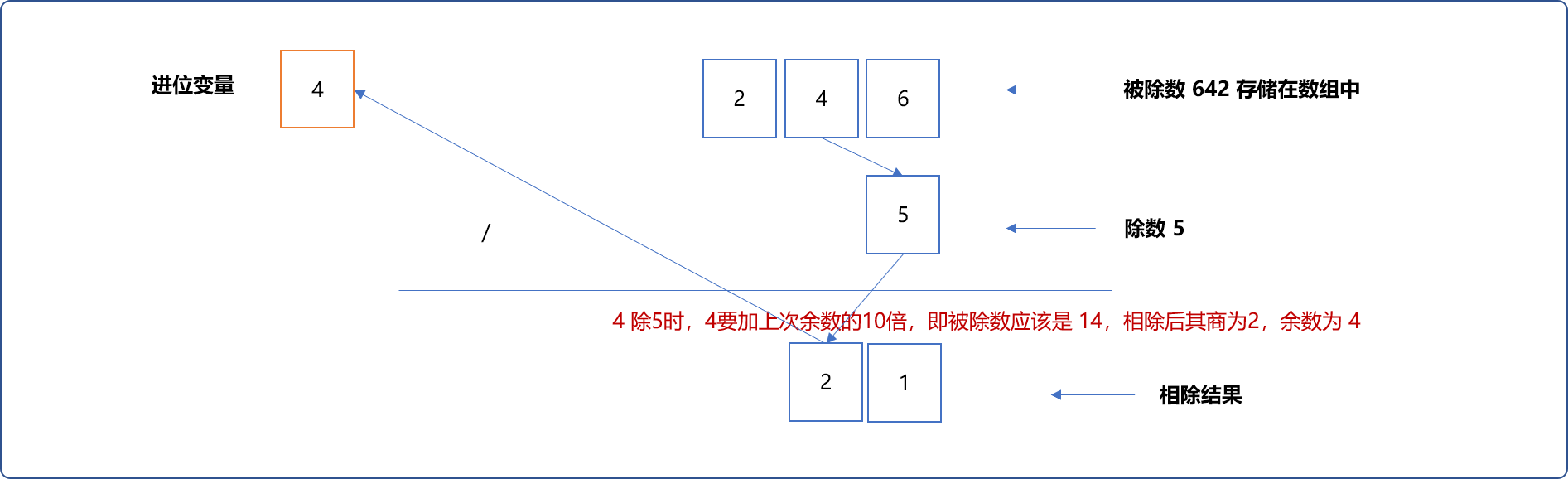
19.png

  • 2除5时如上一样，需要更新被除数后再除。

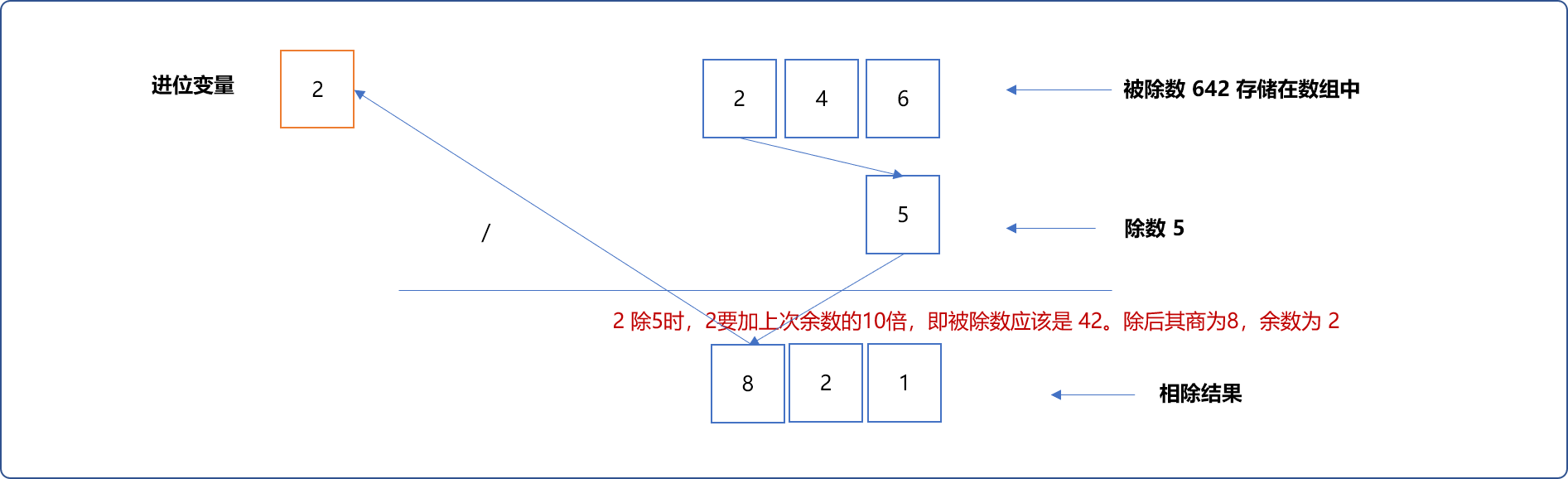
20.png

编码实现：

#include <iostream>
#include <cstring>
using namespace std;
int main(int argc, char** argv) {
	//存储被除数,初始为 0
	int num[100]= {0};
	//除数的长度
	int numLen=0;
	//除数的字符串格式
	string numStr;
	//存储结果
	int result[100]= {0};
	//低精度数字
	int num2;
	cout<<"请输入高精度被除数："<<endl;
	cin>>numStr;
	cout<<"请输入低精度除数："<<endl;
	cin>>num2;
	//转存至数组中
	numLen= numStr.size();
	for(int i=0; i<numLen ; i++) {
		//先计算高位，所以高位存储在数组的前面
		num[i]=numStr[i]-'0';
	}
	//临时变量，存储每次相除的余数
	int temp=0;
	for(int i=0; i<numLen; i++) {
		//每次相除，被除数加上上次相除的余数的10倍
		result[i]= (num[i]+temp*10) / num2;
		temp=(num[i]+temp*10) % num2;
	}
    cout<<"结果：";
	for(int i=0; i<numLen; i++) {
		if(result[i]!=0)
			cout<<result[i];
	}
	cout<<endl<<"余数："<<temp;
	return 0;
}

输出结果：

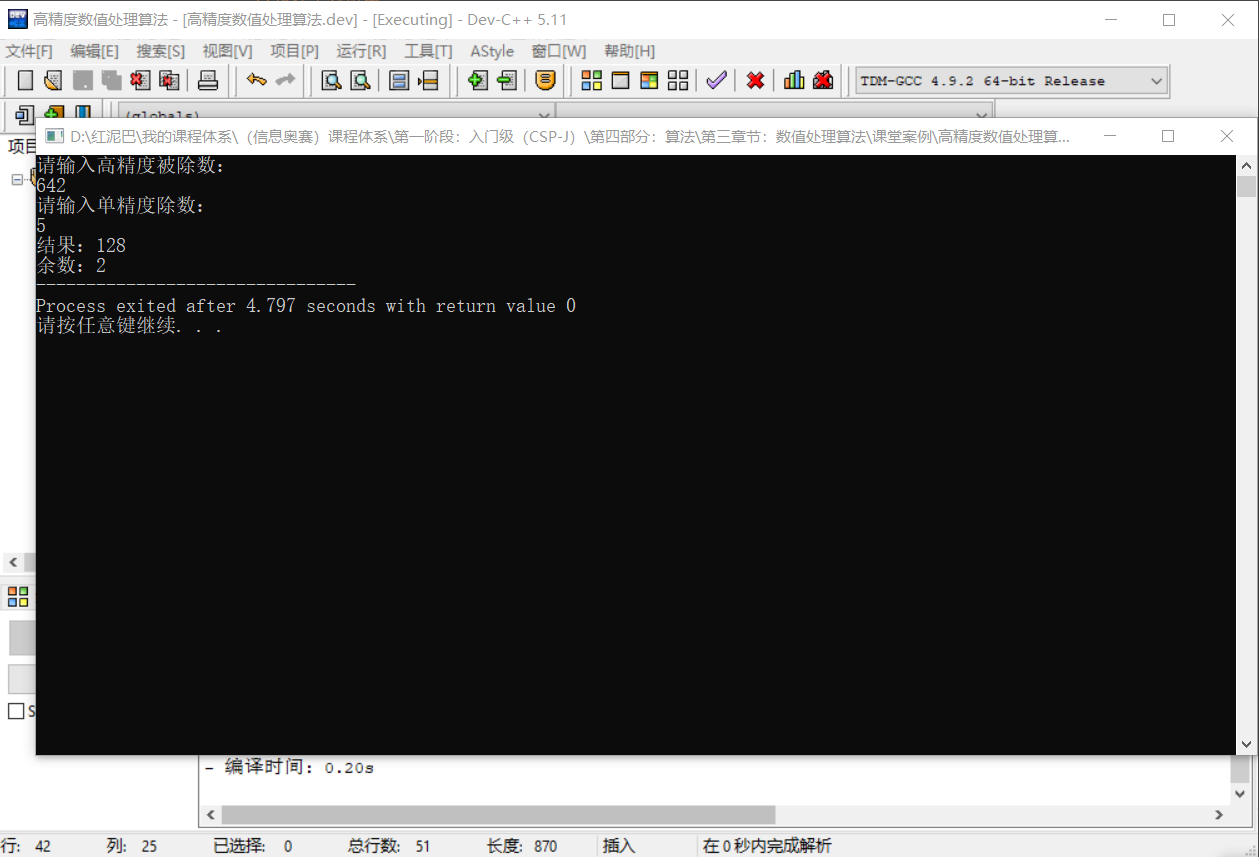
21.png

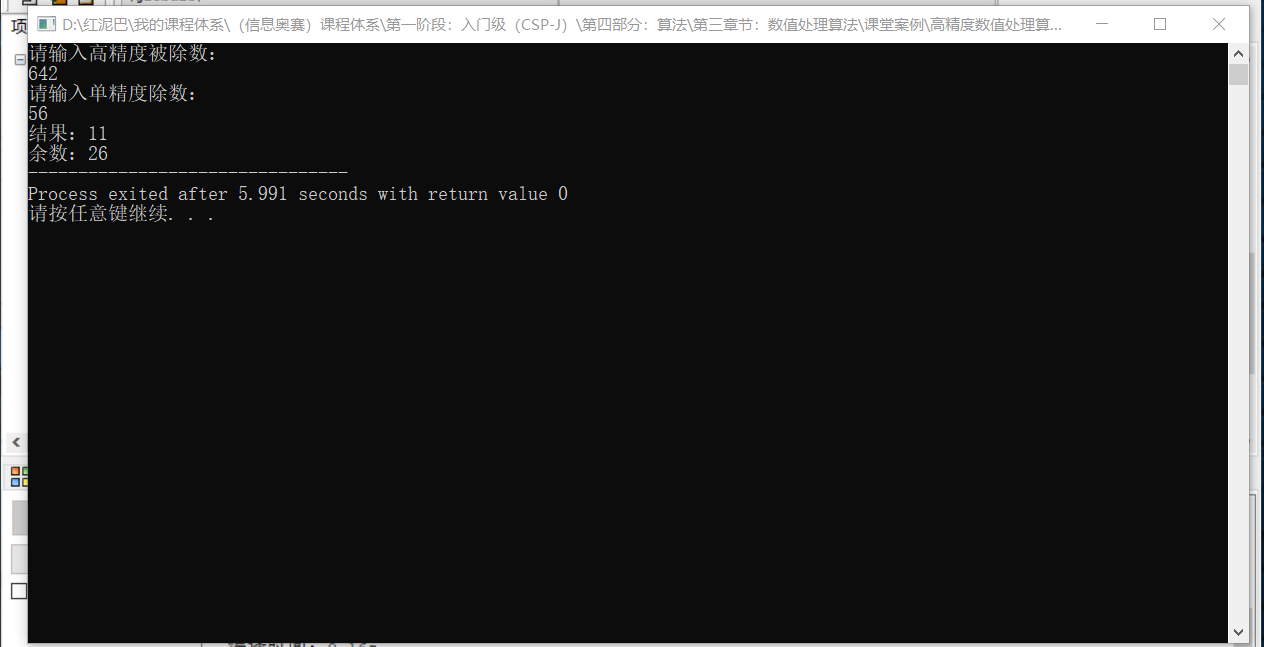
22.png

逐位相除，效率显然是较低的，可以采用一次多位相除方案。可以自行思考。

2.4.2 高精度除以高精度

高精度除以高精度，可以把除法变成减法和加法操作。如：264 除 56的基本思路如下：

  • 第一次： 264-56=208。
  • 第二次：208-56=152。
  • 第三次：152-56=96。
  • 第四次：96-56=40。
  • 第五次：40-56条件不成立，结束相减操作。

当相减的结果小于除数时，不再相减，则264 / 56结果为 4，余数为 40。如上所述，除了不间断地对 2 个数字进行相减，还要统计相减的次数。

**Tips：**从数学角度思考，乘法的本质是加法操作，除法的本质是减法操作。

**编码实现：**代码中有注释，不再另行解释。代码对相减次数做了相应的性能优化。

# include <iostream>
# include <cstring>
using namespace std;
/*
*初始化数组中的值
*/
void stringToNumber(int arr[]) {
	string snum;
	cin>>snum;
	arr[0] = snum.length();
	//用snum[0]存储数字长度
	for(int i=1; i<=arr[0]; i++)
		//将数串s转换为数组	a,并倒序存储
		arr[i] = snum[arr[0]-i] -'0';
}

/*
* 比较 2 个数字的大小
*/
int compare (int num1[],int num2[]) {
	//比较 2 个数字的位数
	if(num1[0]>num2[0]) return 1 ;
	if(num1[0]<num2[0]) return-1 ;
	//位数相同，则从高位向低位逐位比较
	for(int i = num1[0]; i>0; i--) {
		if (num1[i]>num2[i]) return 1 ;
		if (num1[i]<num2[i]) return- 1 ;
	}
	//各位都相等则两数相等
	return 0;
}

/*
* 使用函数封装前面的高精度数值相减算法
* num1-num2的结果存储在 num1 中
*/
void gjdChu(int num1[],int num2[],int result[]) {
	int i, tmp[101];
	result[0] = num1[0] -num2[0]+ 1;
	for (i = result[0]; i>0; i--) {
		int tmp[101]={0} ;
		numcpy(num2,tmp,i);
		while(compare(num1,tmp)>=0) {
			result[i]++ ;   
			gjdJian(num1, tmp) ;
		}
	}
	while(result[0]>0&&result[result[0]]==0)result[0]--;
	return ;
}

/*
*高精度相除
*/
void gjdChu(int num1[],int num2[],int result[]) {
	//结果数值可能的位数
	result[0]=num1[0]-num2[0]+1;
	int count=0;
	//高精度累加的加数，加数只有一个有效的值 1 
	int tem[100]= {0,1};
	//进位值
	int temp=0;
	while  ( compare(num1,num2)>=0 ) {
		gjdJian(num1,num2);
        //统计相减的次数，高精度相加，每次在 result 的个位加 1 
        //如果考虑相除两个数的结果是低精度，由可以直接使用 count++
		for(int i=1; i<=result[0]; i++) {
			//对应位相加
			result[i]=result[i]+tem[i]+temp;
			//存储进位
			temp=result[i] / 10;
			//存储余数
			result[i] %=10;
		}
	}
}
int main(int argc, char** argv) {
	int num1[101]= {0};
	int num2[101]= {0};
	int result[101]= {0};
	stringToNumber(num1);
	stringToNumber(num2);
	gjdChu(num1,num2,result);
	for(int i=result[0]; i>0; i--) {
		if(result[i]!=0)
			cout<<result[i];
	}
	cout<<endl;
	for(int i=num1[0]; i>0; i--) {
		cout<<num1[i];
	}
	return 0;
}

输出结果：

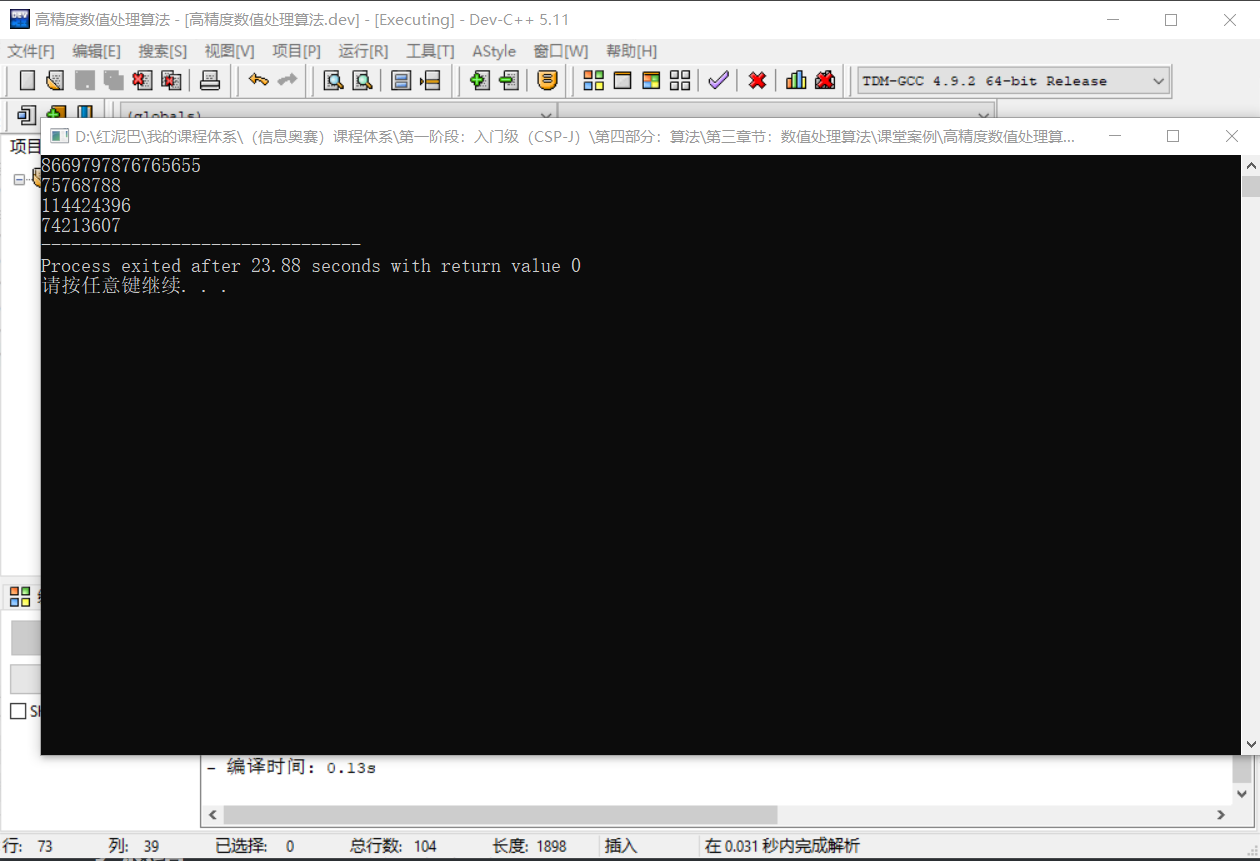
24.png

3. 总结

本文讲解了高精度相加、相减、相乘、相除操作。面对大数值运算时，除了要有好的算法，还需要有低层硬件的支持。在实际进行超高精度数值运算时，可能需要集群环境下并发运算能力的支持。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/36062.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

VMware环境配置

VMware环境配置

文章目录一、环境配置1、修改主机名&#xff0c;然后切换到root用户2、确认主机网关a.确认windows主机网关b.确认虚拟机主机网关3、修改网络配置4、设置DNS域名解析的配置文件resolv.conf。5、修改hosts文件6、重启网络服务7、验证网络服务a.虚拟机ping百度b.主机ping虚拟机二、…
阅读更多...
vscode使用restClient实现各种http请求

vscode使用restClient实现各种http请求

vscode使用restClient实现各种http请求 一&#xff0c;安装插件 首先&#xff0c;我们要在vscode的扩展中&#xff0c;搜索rest Client&#xff0c;然后安装它&#xff0c;这里我已经安装过了。 安装后&#xff0c;我们就可以使用rest client插件进行http各种操作了。 二&a…
阅读更多...
MySQL---权限控制和用户、角色管理详解

MySQL---权限控制和用户、角色管理详解

目录 一、MySQL用户登录 二、用户管理 三、权限控制 四、角色管理 一、MySQL用户登录 一般在本机上我们的登录命令&#xff1a; mysql -u root -p密码这里介绍命令的作用&#xff1a; -u 指定用户名 -h 指定主机地址&#xff08;默认为localhost&#xff09; -p 指定用…
阅读更多...
CHRONY - 时钟同步

CHRONY - 时钟同步

一、同步公网时间源 安装chrony： yum install chrony -y 查看chrony的重要配置文件：rpm -ql chrony 修改chrony配置文件： vim /etc/chrony.conf 查看修改了的配置文件 egrep -v "^#|^$" /etc/chrony.conf
阅读更多...
Baklib知识库|为什么知识共享工具对减少内部知识缺口至关重要

Baklib知识库|为什么知识共享工具对减少内部知识缺口至关重要

你的企业是否存在知识缺口&#xff1f; 知识缺口——没有对关键知识进行研究和记录&#xff0c;以有效地传播信息&#xff0c;并教育企业内外的用户——可能是寻求生产率最大化并最终实现利润增长的公司的一个关键缺陷。知识&#xff08;或数据、关键信息等&#xff09;是你的…
阅读更多...
你一定要知道的四个程序员接外包的网站，悄悄把技术变现！

你一定要知道的四个程序员接外包的网站，悄悄把技术变现！

说起程序员接外包的网站&#xff0c;你在网上一搜发现数不胜数&#xff0c;但真正有用的却很少。然后你想快速的找到几个靠谱的网站&#xff0c;去看了看接外包的攻略&#xff0c;你会发现排雷的又数不胜数。一时间你还真不知道要选哪一个。 接下来就为大家推荐几个我认为比较…
阅读更多...
165 pbi-utils 使用文档

165 pbi-utils 使用文档

165 pbi-utils 使用文档 一、背景 先来说一下为什么会有 pbi-utils 这个小工具吧。在我日常做演示的示例文件的时候&#xff0c;每次都要重新搞一次 Power BI Desktop&#xff0c;就想能不能像 PPT 模板那样&#xff0c;搞一个模板&#xff0c;然后更专心的去专注内容本身呢&…
阅读更多...
网络规划.1.扩展.IP地址规划

网络规划.1.扩展.IP地址规划

第一章 IPv4 Internet中有数百万台以上的主机和路由器&#xff0c;IP 地址可以确切地标识它们。- 一台主机至少拥有一-个IP地址。任何两台主机的IP地址不能相同&#xff0c;但是允许一台主机拥有多个IP地址。如果一台计算机虽然也连入Internet, 使用Internet 的某些功能&#…
阅读更多...
Android 开发中原始音频的录播和和自定义音频控制条的讲解及实战（超详细 附源码）

Android 开发中原始音频的录播和和自定义音频控制条的讲解及实战（超详细 附源码）

需要源码请点赞关注收藏后评论区留下QQ~~~ 一、原始音频的录播 语音通话功能要求实时传输&#xff0c;如果使用MediaRecorder与MediaPlayer组合&#xff0c;那么只能整句话都录完并编码好了才能传给对方去播放&#xff0c;这个时效性太差。 此时用到音频录制器AudioRecord与音…
阅读更多...
[附源码]Python计算机毕业设计二手书交易系统

[附源码]Python计算机毕业设计二手书交易系统

项目运行 环境配置&#xff1a; Pychram社区版 python3.7.7 Mysql5.7 HBuilderXlist pipNavicat11Djangonodejs。 项目技术&#xff1a; django python Vue 等等组成&#xff0c;B/S模式 pychram管理等等。 环境需要 1.运行环境&#xff1a;最好是python3.7.7&#xff0c;…
阅读更多...
企业如何提供安全方面的投资回报率？

企业如何提供安全方面的投资回报率？

为什么增加在恢复方面的投资可以提高投资回报率? 所有企业都会认可安全的重要性&#xff0c;但在安全上的投入却经常令人迷惑。 一方面&#xff0c;由于安全威胁在不断变化&#xff0c;所以&#xff0c;安全建设维护需要长期持续大量投入。另一方面&#xff0c;长期大量投入后…
阅读更多...
第6章 集成第3方依赖注入中间件“Autofac”

第6章 集成第3方依赖注入中间件“Autofac”

“Blog.Core-master”示例程序中接口及其具体实现类的注入操作&#xff0c;是通过第3方依赖注入中间件“Autofac”来以反射方式把Service.dll 程序集中所有接口及其具体实现类的实例依赖注入内置容器中。.Net(Core).x框架是中的内置依赖注入容器是不支持程序集注入的。 从最佳实…
阅读更多...
葡萄糖-聚乙二醇-人血清白蛋白,HAS-PEG-Glucose,人血清白蛋白-PEG-葡萄糖

葡萄糖-聚乙二醇-人血清白蛋白,HAS-PEG-Glucose,人血清白蛋白-PEG-葡萄糖

葡萄糖-聚乙二醇-人血清白蛋白,HAS-PEG-Glucose,人血清白蛋白-PEG-葡萄糖 人血清白蛋白(HSA)是一种高度水溶性的球状单体血浆蛋白&#xff0c;相对分子量为67KDa&#xff0c;由585个氨基酸残基、一个巯基和17个二硫键组成。在纳米颗粒载体中&#xff0c;HSA纳米颗粒与各种药物…
阅读更多...
直播预告丨中高频多因子库存储的最佳实践

直播预告丨中高频多因子库存储的最佳实践

因子挖掘是量化交易的基础。随着历史交易数据日益增多&#xff0c;交易市场量化竞赛的不断升级和进化&#xff0c;量化投研团队开始面对数据频率高、因子数量多的场景&#xff0c;以10分钟线10000个因子5000个股票为例&#xff0c;一年的因子数据约为 2.3T 左右&#xff0c;1分…
阅读更多...
BUUCTF Reverse/firmware

BUUCTF Reverse/firmware

安装工具firmware-mod-kit &#xff0c;可以参考这个firmware-mod-kit工具安装和使用说明 最后make的时候报了个错&#xff0c;参考这个&#xff1a;linux安装firmware-mod-kit /firmware-mod-kit/src/uncramfs/uncramfs.c 加上头文件&#xff1a;#include <sys/sysmacros.h…
阅读更多...
想做TikTok跨境电商？如何运营？

想做TikTok跨境电商？如何运营？

想做TikTok跨境电商&#xff1f;如何运营&#xff1f; 据官方报道&#xff1a; 2021年8月TikTok全球月活跃用户数已突破10亿 自2020年7月以来增长了45% 相比2020年初则增长了一倍 月活跃用户能达10亿&#xff0c;覆盖150个国家地区 你只要爆了一条视频 分一小杯羹就能舒…
阅读更多...
13.5 GAS与连击

13.5 GAS与连击

目录1. 连击检测窗口与砍出的第二刀1. 连击检测窗口与砍出的第二刀 连击的实现思路是&#xff0c;在劈砍动画的期间的某一段窗口期&#xff0c;令角色能够再次响应输入&#xff0c;完成伤害动作并进入新的连击动画&#xff0c;直到连招打完。所以核心关键就在于这一段连击窗口…
阅读更多...
Halcon机器视觉实战--分水岭分割+距离变换实现粘连物体图像分割

Halcon机器视觉实战--分水岭分割+距离变换实现粘连物体图像分割

分水岭的原理 把图像的灰度看作高度图，图像中每个像素点的灰度值看作该点的高度，高灰度值代表山脉，低灰度值代表盆地，每个局部最小值及其周围区域称为集水盆，而集水盆的边界则形成分水岭。 分水岭算法的步骤 1.彩色图像转化成单通道灰度图 2.求梯度图 3.在梯度图的基础…
阅读更多...
BCH编码译码误码率性能matlab仿真

BCH编码译码误码率性能matlab仿真

目录 1.算法描述 2.仿真效果预览 3.MATLAB部分代码预览 4.完整MATLAB程序 1.算法描述 BCH编译码是一种纠错能力强&#xff0c;构造简单的信道编译码。BCH编译码的生成多项式可以由如下的式子表示&#xff1a; ①BCH码是一种纠错码、线性分组码、循环码。 ②需要传输信息位…
阅读更多...
如何搭建一个好的知识库管理系统？

如何搭建一个好的知识库管理系统？

简道云知识管理应用对于想知道怎样搭建一个好的知识库管理系统的人来说&#xff0c;拥有正确的流程非常重要。这个过程不需要很复杂&#xff0c;但如果您想要个满足更多需求的知识管理系统&#xff0c;它确实需要非常的全面。 简道云知识库&#xff1a;http://s.fanruan.com/r…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023