智慧税务解决方案-最新全套文件
- 一、建设背景
- 税务大数据现状和挑战
- 1、数据割裂,外部数据整合不足,智能化应用不足
- 2、缺乏统一治理,数据资产不清,质量不高
- 3、数据获取效率低,数据冗余、查询效率低
- 4、 运营运维体系不健全,运营挑战大
- 二、建设思路
- 三、建设方案
- 四、获取 - 智慧税务全套最新解决方案合集
一、建设背景
税务大数据现状和挑战
1、数据割裂,外部数据整合不足,智能化应用不足
- 批量数据汇聚,无法满足实时数据汇聚业务需要;
- 纳税人相关数据分散在各个模块的不同数据表里,没有整合和关联;
- 政府其他部门数据和互联网第三方数据整合不足。
2、缺乏统一治理,数据资产不清,质量不高
- 在数据治理工具、数据治理专业服务和数据服务能力上不足;
- 缺乏可视化的基础数据资产管理,无法支撑数据血缘关系管理、业务建模和数据可视化分析。
3、数据获取效率低,数据冗余、查询效率低
- 业务部门在进行数据分析时,获取数据的方式比较原始,通常需要编写脚本到数据库中查询或是通过金三系统前台页面多次查询数据;
- 缺乏数据和分析工具,不能充分释放出基层的业务创新额潜力。
4、 运营运维体系不健全,运营挑战大
- 数据应用、数据管控等的管理办法、管理流程、管理规范(技术和业务规范),有缺失;
- 各地运维团队缺失,无法有效支撑平台运营工作。
二、建设思路
1.数据汇聚
- 统一税务局和其他政府部门的数据采集交换平台
- 提升数据接入场景能力,提供批量、实时、流式多种数据集成方式
- 建立第三方数据采集通道和管理规范
2.存储计算
- 建设多种类型存储计算,满足批量计算、流计算、交互式查询、实时检索等多种计算场景;
3.数据治理体系
- 建设一体化数据治理工具体系
- 优化数据管理组织与职责,梳理数据资产,建立数据资产管理机制,明确数据标准落地执行机制
- 建设数据质量管理体系,持续加强数据治理
4.统一分析工具
- 建设自助式BI分析和标签工具,数据潜能快速释放;
- 建设一站式人工智能平台,助力税务智能化转型;
5.统一数据服务
- 建设统一数据服务管控,提供工具服务以及数据服务,实现数据快速变现;
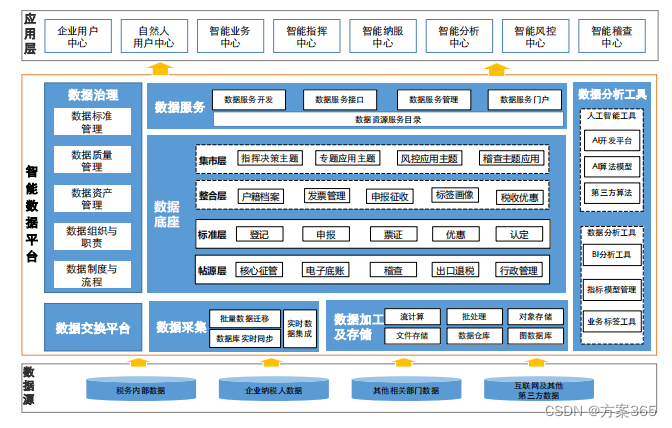
三、建设方案
- 核心是让数据形成数据资产,易懂、易用,让数据真正用起来;
- 有效解决数据质量问题,提升数据质量;
- j建设可视化数据管理平台工具;
- 实现对数据的有效管理,提升数据质量,建立数据共享机制。
- 建立和完善数据管控的组织架构、制度和流程;
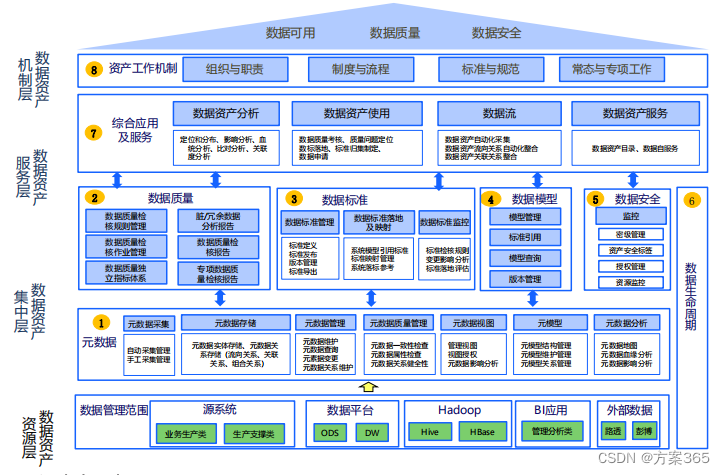
四、获取 - 智慧税务全套最新解决方案合集
提示:智慧税务等,300+行业最新解决方案,点击下方链接获取。