链式二叉树是由指针形成的二叉树,之前写的二叉树是由数组组成的,链式由链表来做。链式二叉树每个节点有两个指针,指向两边。以往二叉树,栈,队列等等都需要增删查改,但链式二叉树则不是这样,是因为由于链表结构,它没办法很好地增删查改。所以这里要写的并不是和数组二叉树一样的结构,而是一颗搜索树,左子树比根节点小,右子树比根节点大。这样插入一个数值就可以安放的位置,想要搜索某个数也可以选择一颗来往下查找,这样查找的效率也就是树的高度次。搜索二叉树也就有了增删查改的意义,以及也可以进行遍历了。像之前写的二叉树并不能用来遍历,或者说也没有任何意义,而搜索二叉树则可以展示两个子树各自的情况。
我们先来看搜索二叉树的四种遍历方法
前中后序(根)以及层序遍历
搜索二叉树一个思路就是一个根节点只管自己的两个子节点,其他一概不管。
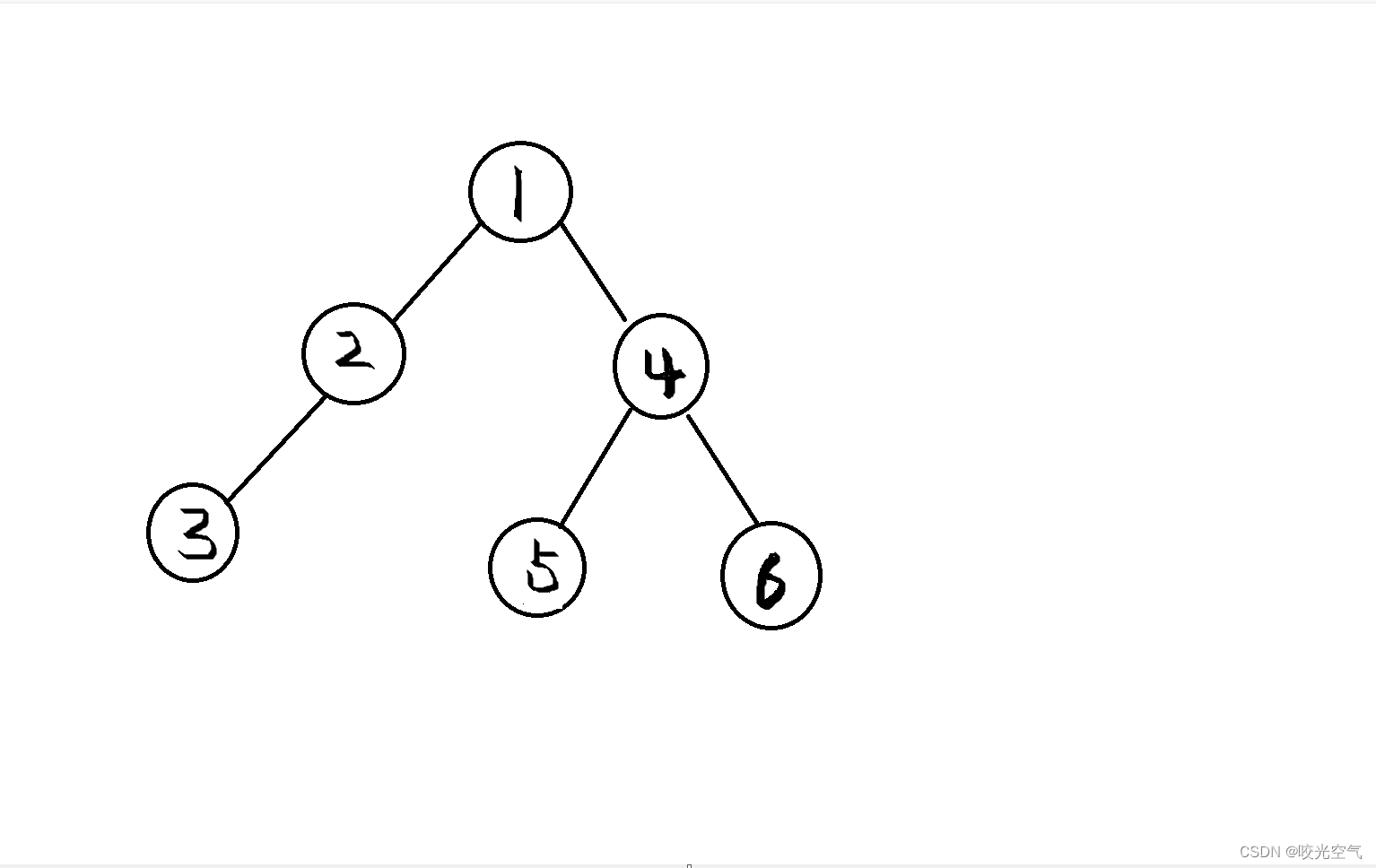
关于前序,顺序为根,左子树,右子树:1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL。
分析一下这个前序,从根走起,然后再走左子树,也就是1 2 ,之后走到3,3的左子树是NULL,那么再看3的右子树,也是NULL,那么3这里就结束了,出现了两个NULL,回到2,3是2的左子树,那么再看2的右子树,是NULL,回到1,所有出现了1 2 3 NULL NULL NULL。那么再访问1的右子树,4,访问左子树5,5的左右子树都是NULL,所以有 4 5 NULL NULL,再看6,6后面也是两个NULL,所以最后整个顺序就出来了。
关于中序,顺序为左子树,根,右子树:NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
关于后序,顺序为左子树,右子树,根:NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
关于层序,从第一层开始,每层从左到右,一层层访问:1 2 4 3 5 6
现在我们从代码角度理解这种二叉树。
这个二叉树由链表构成,所以
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
int main()
{
BTNode* root;
}
搜索二叉树的实现会用到递归。遍历时,整个数的根节点和它的子节点遍历完后,再以子节点为根节点,继续向下遍历,所以整体用递归更适合。
我们先写前序遍历。如果root本身就为空,那么就把直接返回空;不为空的情况下,由于顺序为根,左子树,右子树,那么我们需要先打印一下根节点元素,然后左下走,如果左面走完了再走右面,然后我们还得回来再走整个数的右子树。代码如下:
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
尽量画图理解递归过程,这里就不写了。呈现出来有点麻烦。
我们先测试一下,写个创建结构体函数。
BTNode* BuyBTNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
exit(-1);
}
node->data = x;
node->left = node->right = NULL;
return node;
}
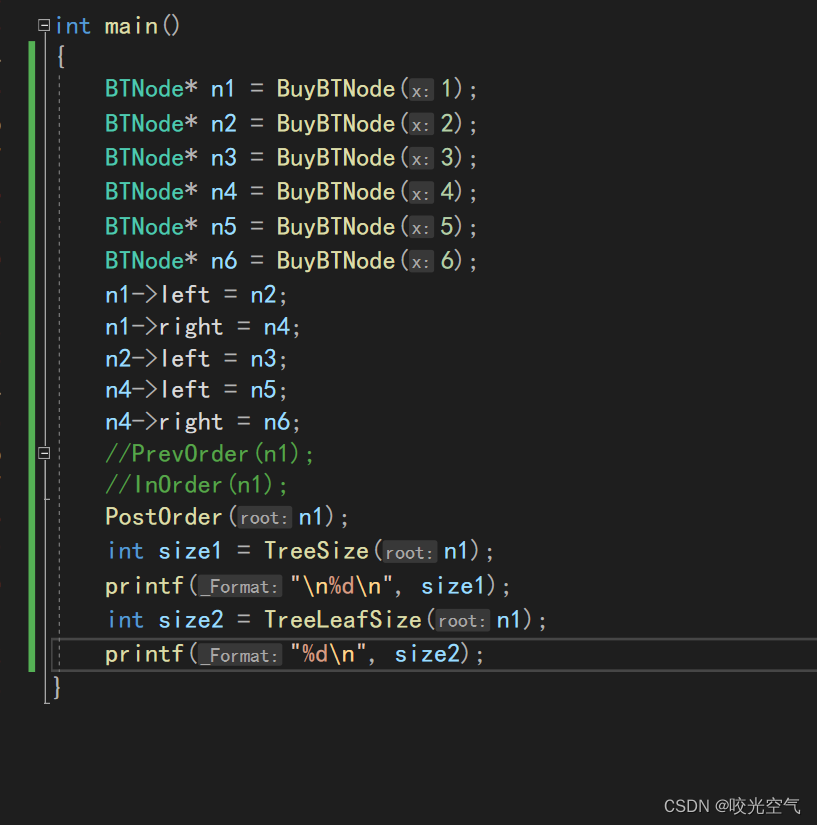
然后测试,我们手动写出关系
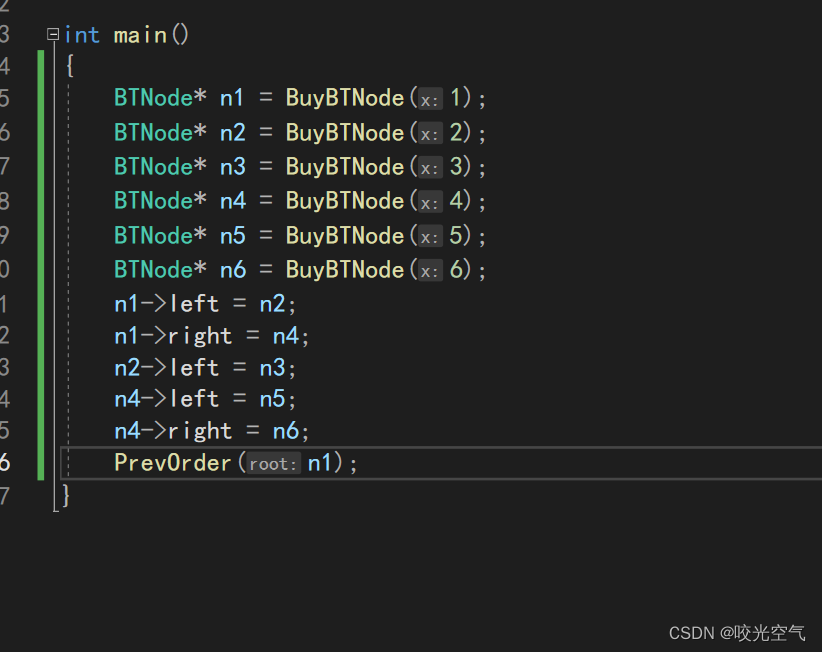
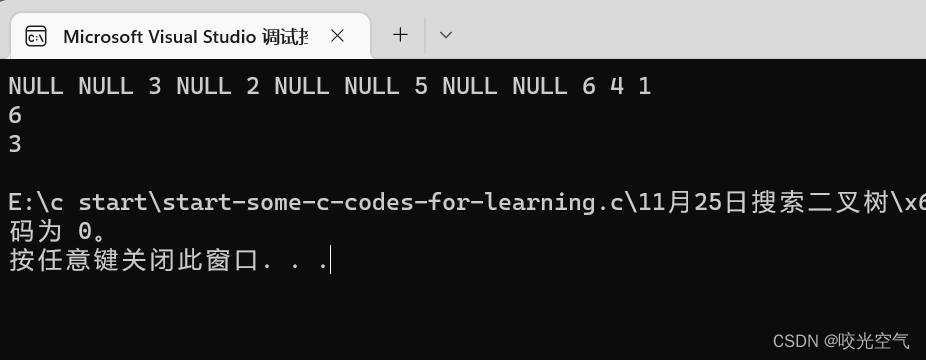
结果如下
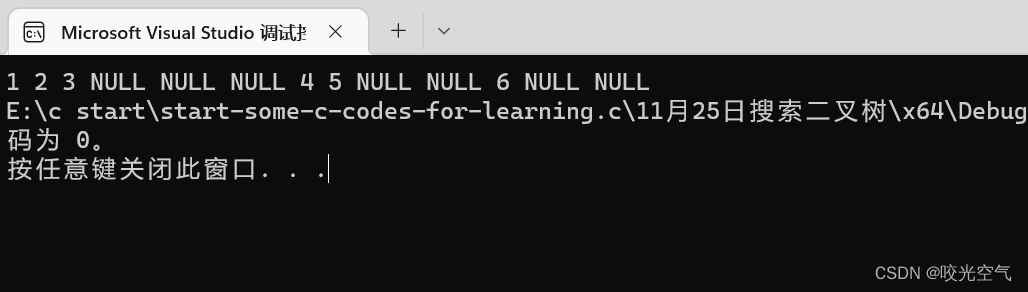
所以接下来中序,后序也都好写了。
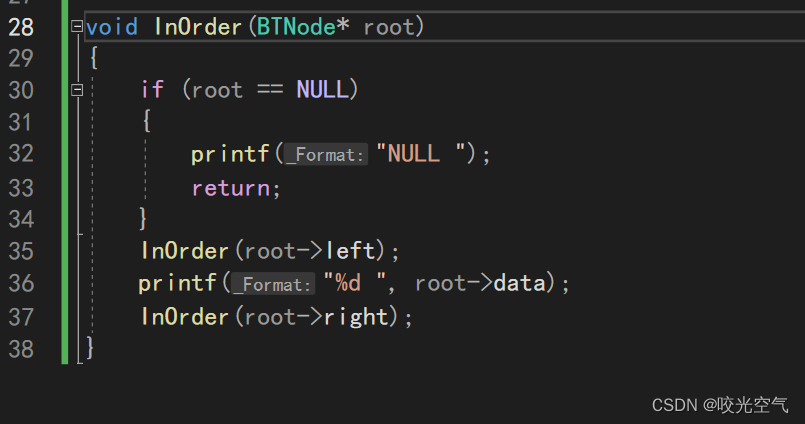
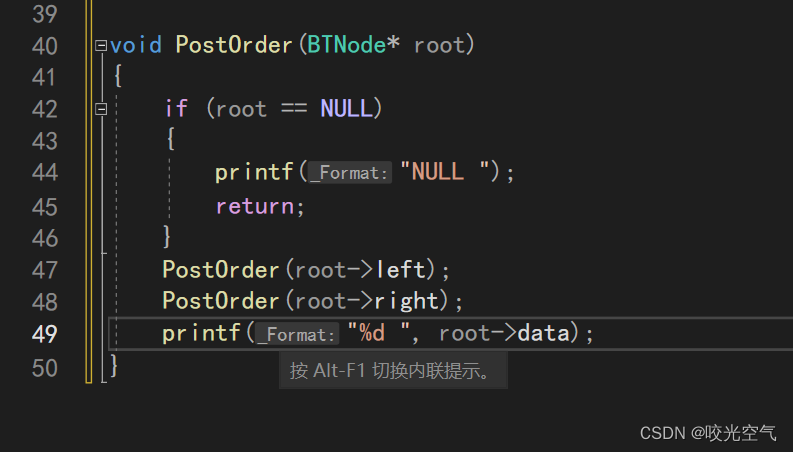
现在解决一些难题
1、求二叉树节点个数
能够很快想到的办法就是遍历一遍,数出节点个数,不是NULL就size++一次。但是我们不能直接这样
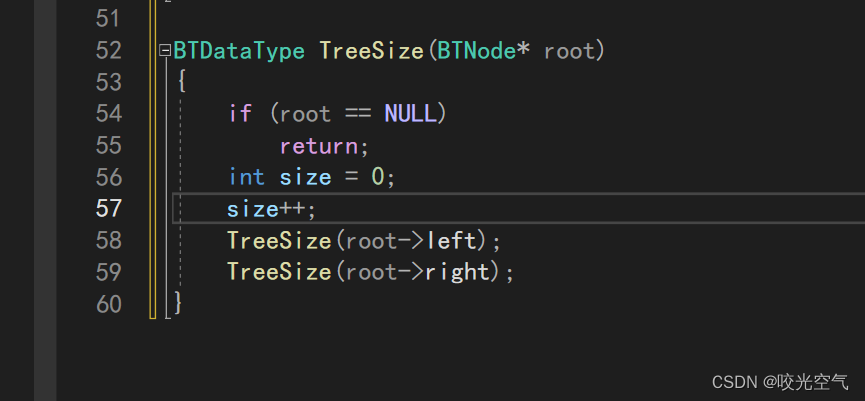
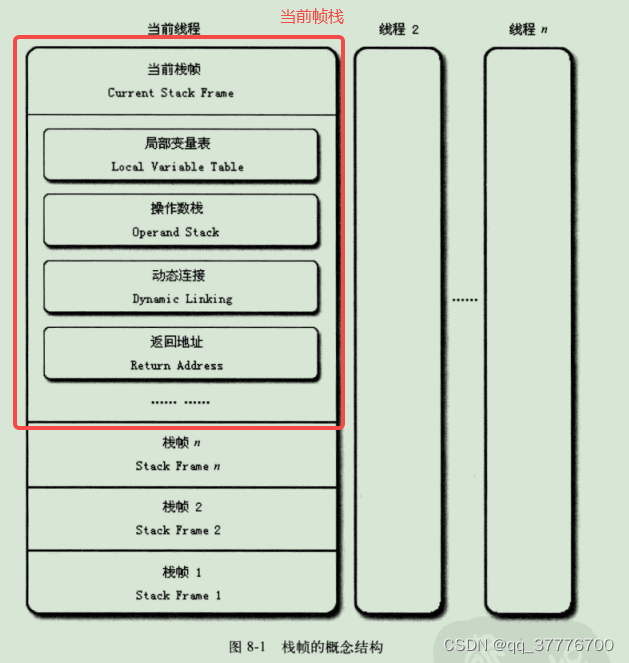
每一次递归,都会开一块栈帧,每一块空间size都为0,所以最后根本不是我们要的结果。那如果static一下如何?static int size,size在静态区,确实不会受递归影响,但是同样也不受我们控制了,当多次调用后,size会一直加下去,也不是我们要的数字。不过size可以定义成全局变量,每次调用前都设为0,不过这个办法也有点麻烦。
关于计算节点个数,同样也可以用之前的思路,一个根节点管两个子节点,为空就0,不为空就传回来数字
BTDataType TreeSize(BTNode* root)
{
return root == NULL ? 0 : 1 + TreeSize(root->left) + TreeSize(root->right);
}
画图就能理解这个代码
增加一下难度,求叶子节点的个数
虽然这个问题的思路和之前异曲同工,但是不能这样写
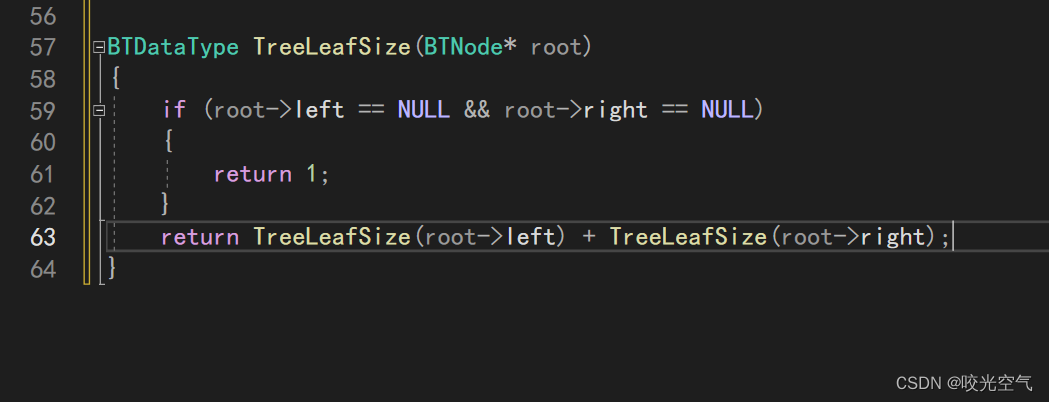
程序最终会停在那里,然后直接退出。这是为什么?我们就着这个图再看
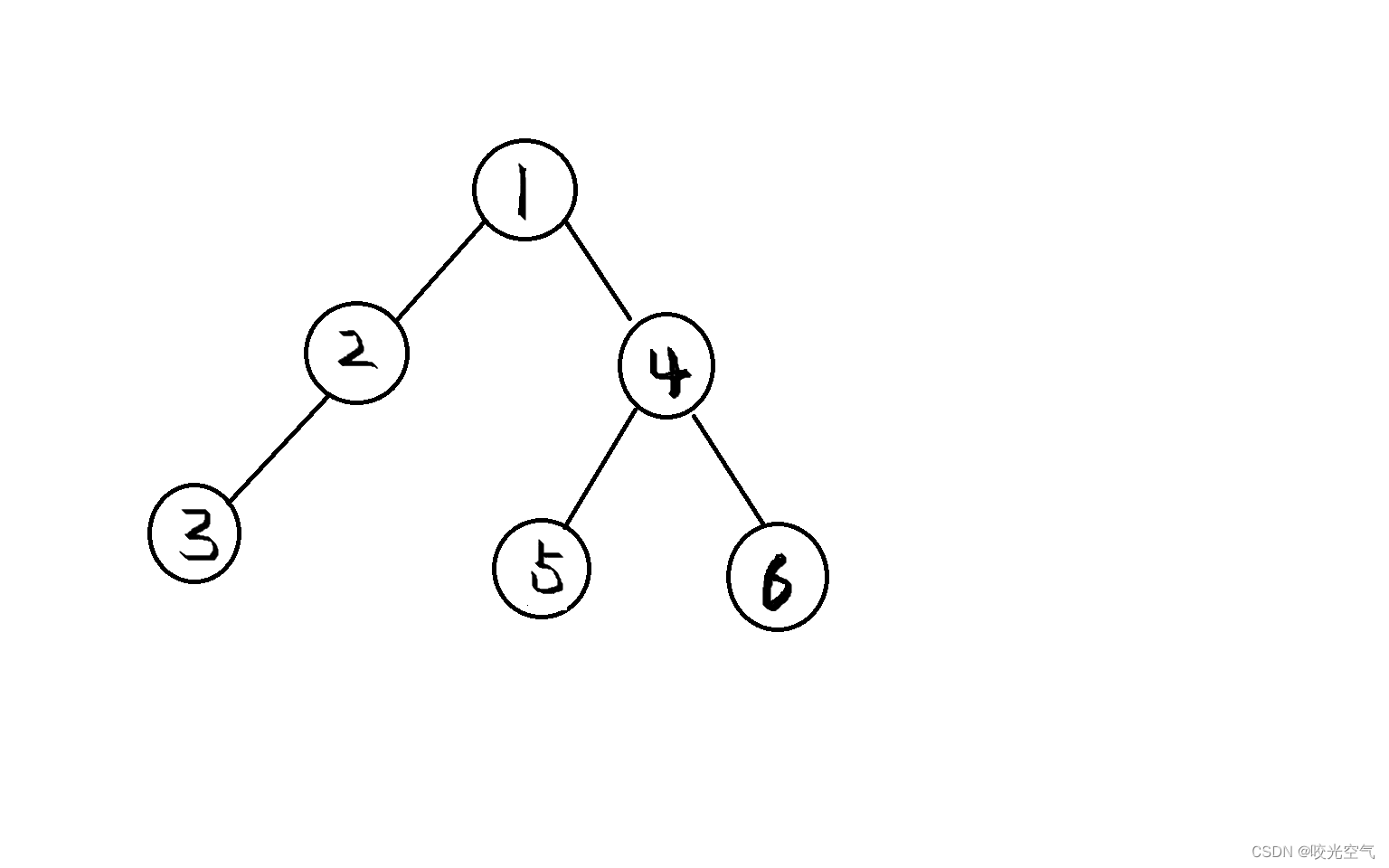
1的两个子节点都不是空,找到2,2同样也不是叶节点,找到3,3是叶节点,返回1,再回到2,访问2的右子节点,这时候就出问题了,本身这个节点就是NULL,然后程序还在判断它的左右子节点为不为空,程序就崩了。
所以我们必须要在判断左右前先判空
if (root == NULL)
return 0;
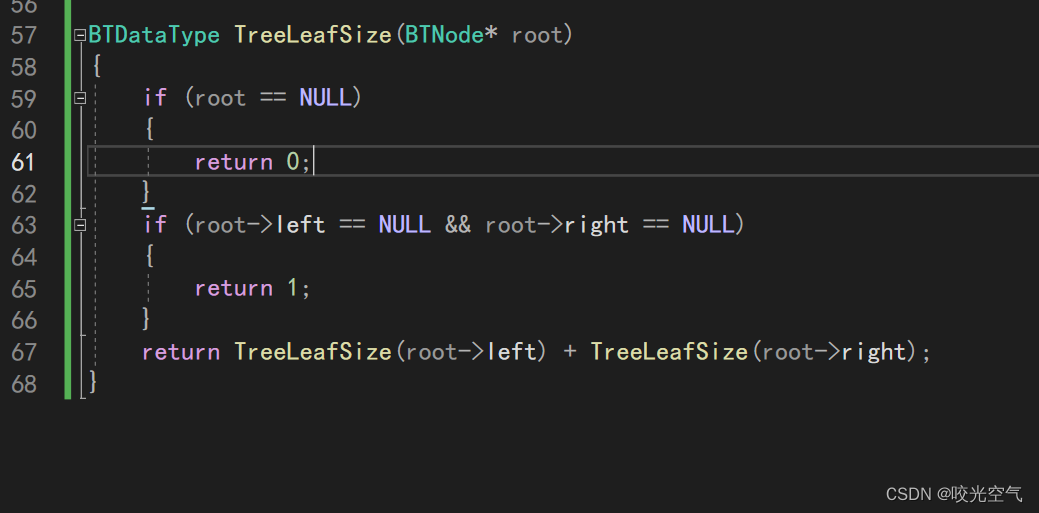
这样整个代码就对了。 我放上一整段测试代码
2、求树的深度(高度)
默认根从1开始。
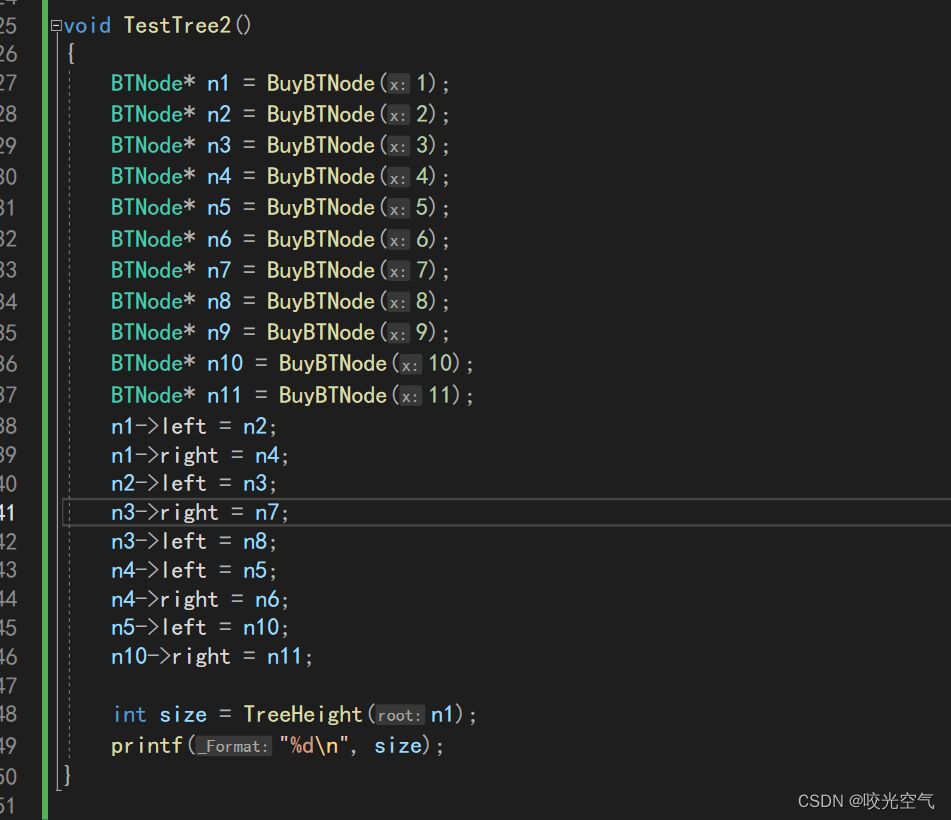
先把原先的图增加一层
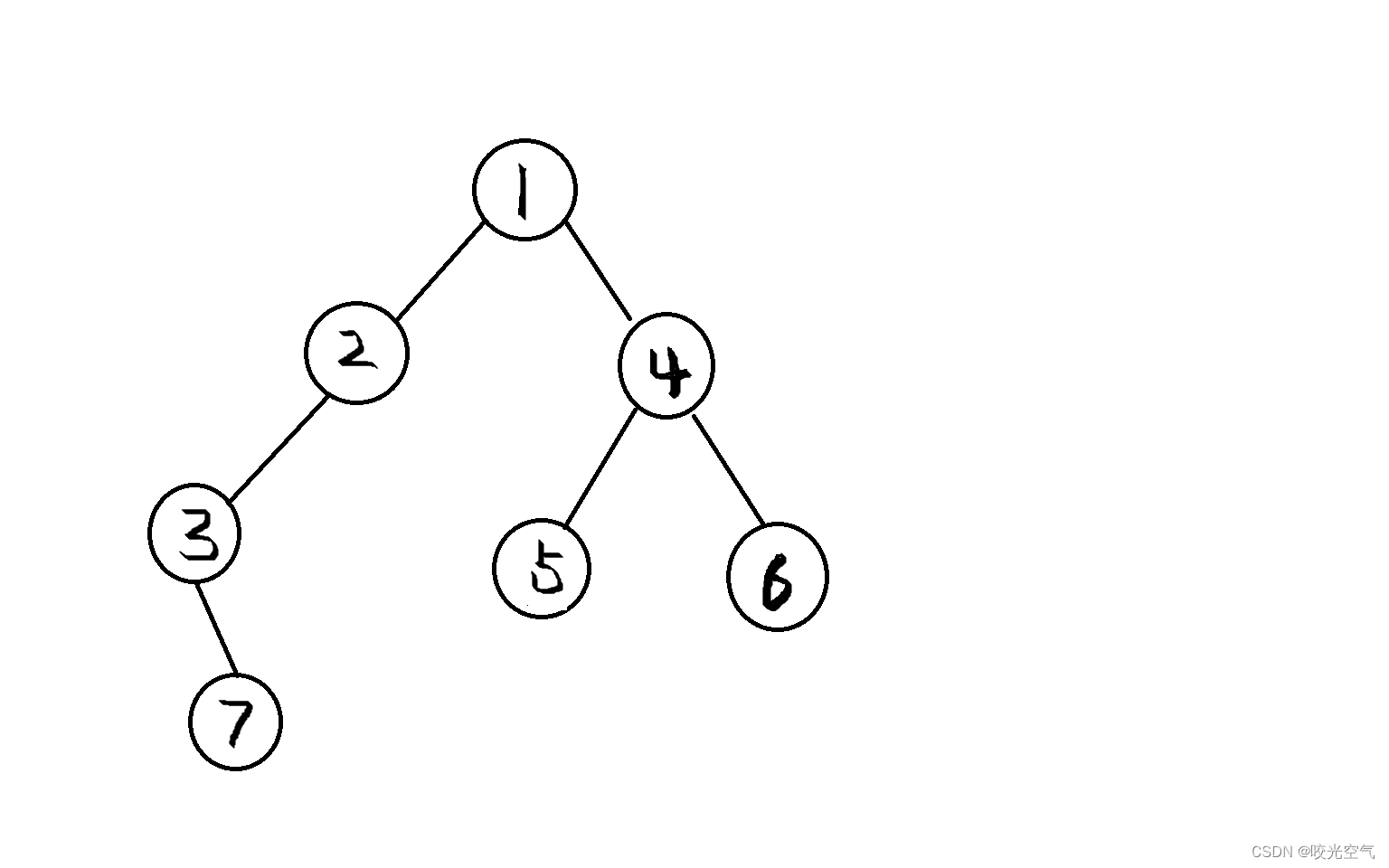
左右子树并不一定同样高度,我们就需要算出两个高度,然后比较一下即可。
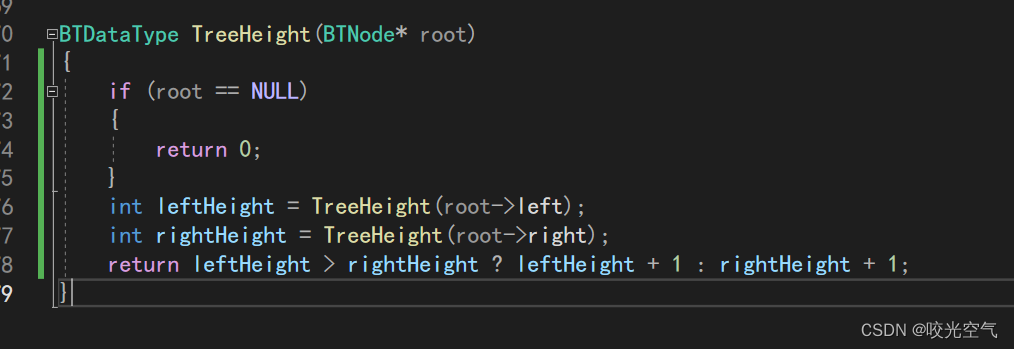
测试代码
3、求第k层的节点个数 k >= 1
其实也是要分左右子树啊,但是和层序没有关系啊,这个题不需要层序。这里提供一个想法,第k层是相对于第1层的第k层,那对于第2层来说,那就是第k-1层,第k层的节点个数就等于左子树的第k-1层节点个数 + 右子树的第k-1层节点个数。遇到NULL就返回0。如果k为1,一个是本身就统计的祖先层,一个是相对来说是第一层,意思就程序已经来到第k层,那么这时候就相对来说是第1层,返回1.
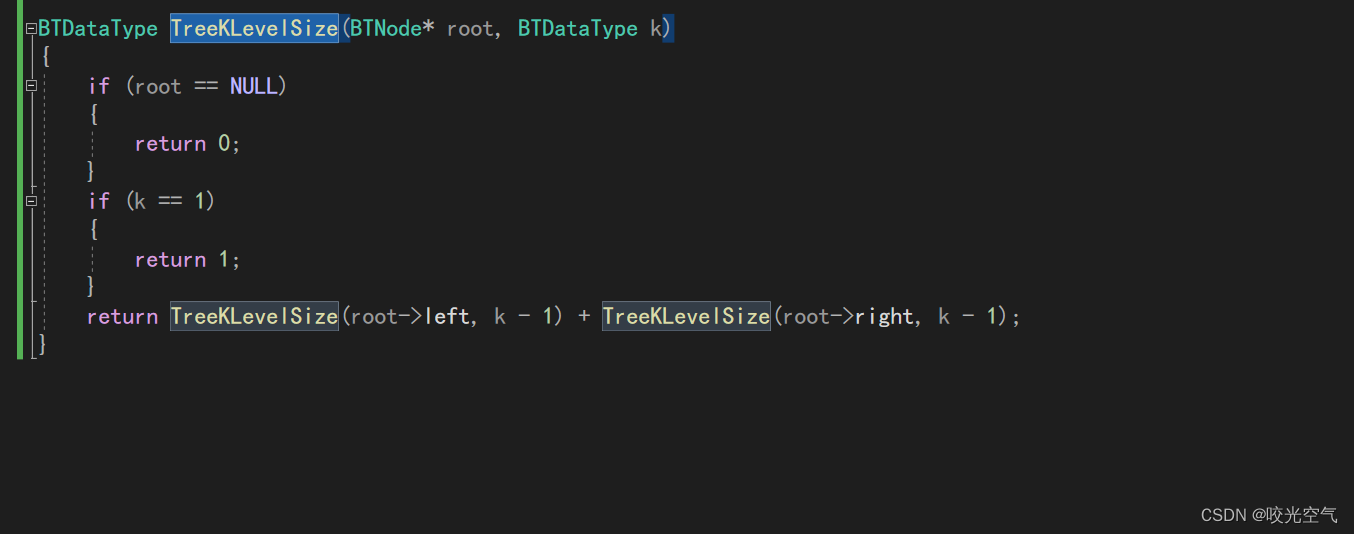
测试代码
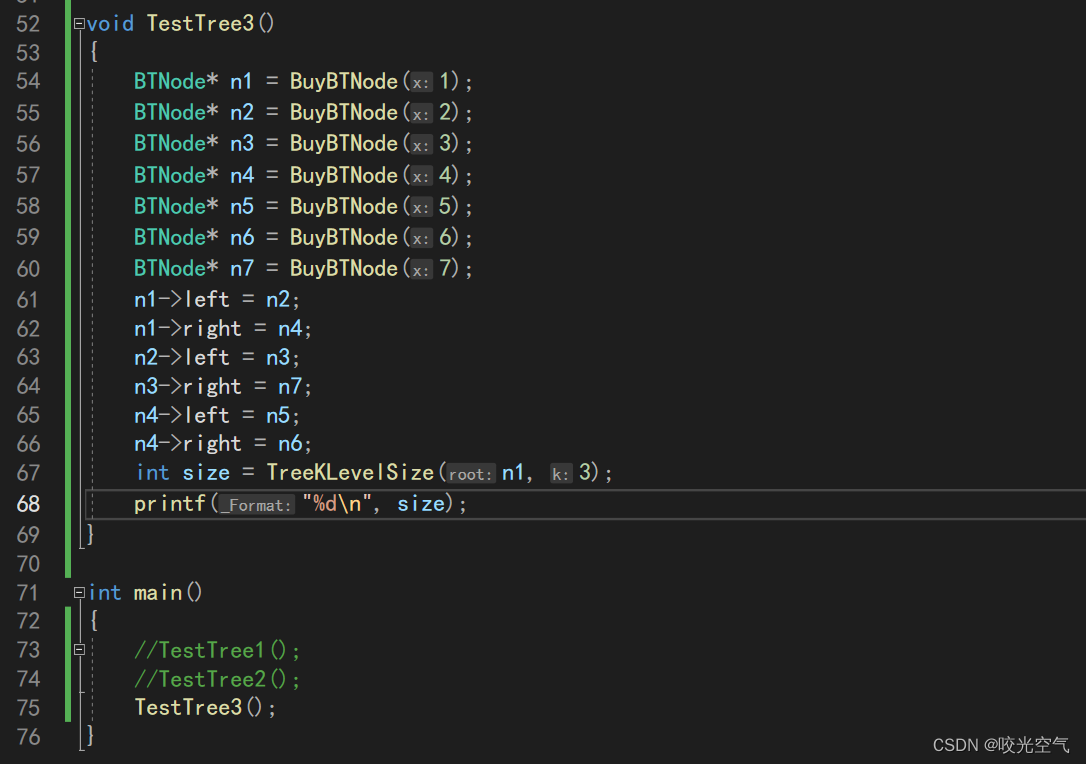
我们还是用上面那个白图。
最终结果就是3.
4、查找值为x的节点
当然,还是递归。不过经历上面的问题,可以发现,关于具体数值的问题,我们就不能直接递归,需要在递归过程中用一个变量存储值才行。这个问题同样如此。
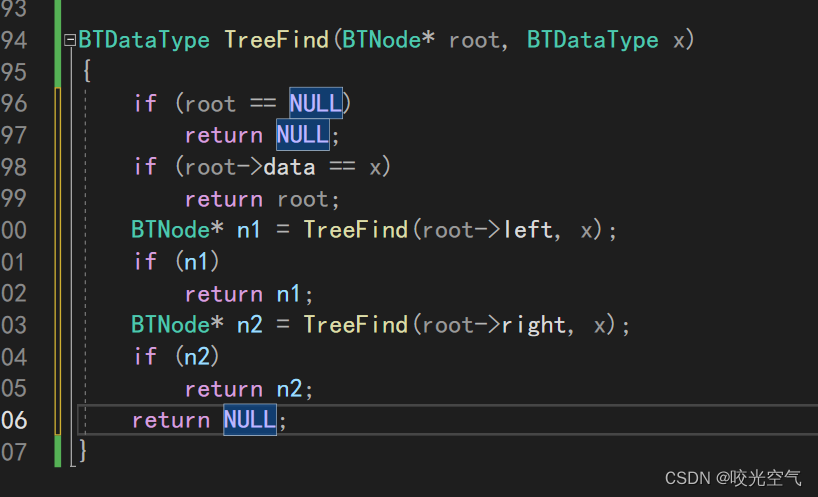
根据以上问题,慢慢理解二叉树的结构。
结束。






![[附源码]计算机毕业设计JAVA乒乓球俱乐部管理系统](https://img-blog.csdnimg.cn/a7e7adfe53ab4b419541e442423d2666.png)