本文仅供学习使用
本文参考:
《机构运动微分几何学分析与综合》-王德伦、汪伟
《微分几何》吴大任
Ch02-2 平面机构离散运动鞍点综合
- 2.3 鞍点圆
- 2.3.1 鞍圆与二副连架杆R-R
- 2.3.2 鞍圆误差
- 2.3.3 四位置鞍圆
- 2.3.4 五位置鞍圆
- 2.3.5 多位置鞍圆
2.3 鞍点圆
平面连杆机构中有两类连架杆R-R和P-R,其约束曲线分别为圆和直线。就平面四杆机构综合而言,就是在平面离散运动刚体上寻找特征点,使其在固定坐标系中的轨迹与约束曲线(圆和直线)的差异尽可能小,从而形成四杆机构。运动刚体上点产生的轨迹由一系列离散点组成,少则三到五个,多至几十或百千个,离散轨迹的几何性质取决于刚体的离散运动性质与点在刚体上的位置。平面离散运动几何学研究离散运动刚体上点及其离散轨迹的整体几何性质(与圆或直线的差异),其中圆点与滑点是少位置情形的经典理论,而多位置运动刚体上点及其离散轨迹几何性质的变化,尚在讨论之中。本节以最大误差最小评价准则建立鞍点规划模型,讨论运动刚体上点及其离散轨迹曲线逼近圆的性质。
2.3.1 鞍圆与二副连架杆R-R
对于给定平面运动刚体 Σ ∗ \Sigma * Σ∗在固定坐标系 { O f ; i ⃗ f , j ⃗ f } \{{{O}_{f}};{{{\vec{i}}}_{f}},{{{\vec{j}}}_{f}}\} {Of;if,jf}中的一系列离散位置,运动刚体上点 P ( x P m , y P m ) P({{x}_{Pm}},{{y}_{Pm}}) P(xPm,yPm)在固定坐标系中的轨迹为离散点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)},在此讨论轨迹离散点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}与圆的近似程度。依据平面圆曲线的不变量性质,圆的曲率为常数(圆心位置由曲线曲率中心确定),常规意义上的圆心到圆上任一点的距离为常数仅是坐标系中的一种表现形式。
那么,用一圆来拟合点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)},对于给定圆心位置和半径的圆拟合,称为固定圆拟合,拟合结果的最大误差必然与圆心位置及半径
r
r
r有关,拟合效果具有偶然性;
如果仅给定半径
r
r
r,圆心位置由点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}的性质自适应确定,使得最大拟合误差为最小,如下图所示,得到与点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}最接近的圆,称为浮动圆拟合。不同半径的浮动圆拟合有不同的误差,其中必有一个使得最大法向拟合误差为最小的最佳浮动圆拟合,其实是离散点集(曲线)的不变量,不随所在坐标系变化而变化。
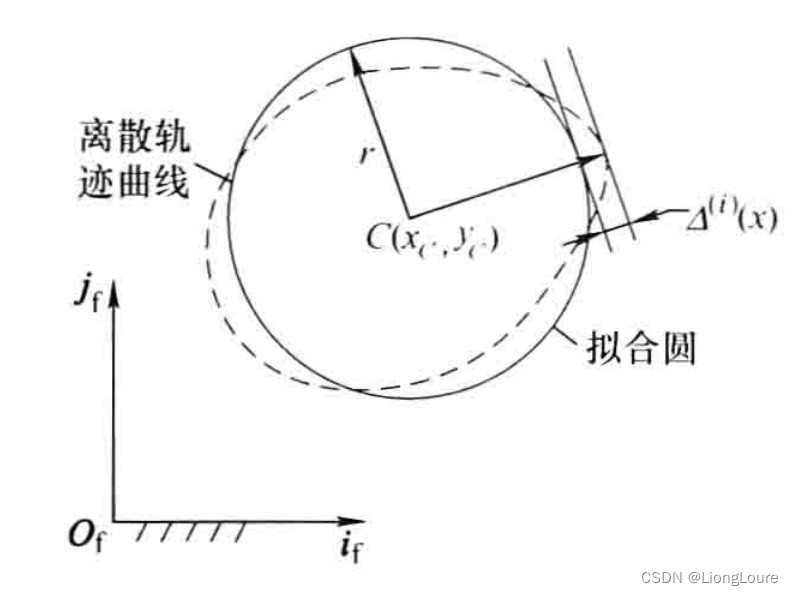
定义2.1 依据被拟合离散点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}的性质并按最大法向拟合误差最小为原则得到唯一的拟合圆,称为
鞍圆,其对应的最大法向拟合误差称为鞍圆误差。
显然,鞍圆的半径大小和圆心位置由被拟合点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}的性质并按最大法向拟合误差为最小原则确定,是点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}所有拟合圆中最大法向误差最小的拟合圆,再也没有更合适的圆来拟合点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}使得拟合的最大误差更小。具有最大法向误差最小的意义,即一次鞍点意义,这里的误差也是曲线的不变量,与曲线所在坐标系无关。为此,建立鞍圆拟合模型∶
{
Δ
=
min
X
max
1
≤
i
≤
n
{
∣
Δ
(
i
)
(
x
)
∣
}
=
min
X
max
1
≤
i
≤
n
{
∣
(
x
P
(
i
)
−
x
C
)
2
+
(
y
P
(
i
)
−
y
C
)
2
−
r
∣
}
s
.
t
.
r
∈
(
0
,
+
∞
)
x
=
(
x
C
,
y
C
,
r
)
T
\left\{ \begin{matrix} \Delta =\underset{X}{\mathop{\min }}\,\underset{1\le i\le n}{\mathop{\max }}\,\{\left| {{\Delta }^{(i)}}(x) \right|\}=\underset{X}{\mathop{\min }}\,\underset{1\le i\le n}{\mathop{\max }}\,\{\left| \sqrt{{{(x_{P}^{(i)}-{{x}_{C}})}^{2}}+{{(y_{P}^{(i)}-{{y}_{C}})}^{2}}}-r \right|\} \\ \begin{matrix} s.t. & \begin{matrix} r\in (0,+\infty ) & {} \\ \end{matrix} \\ \end{matrix} \\ \begin{matrix} {} & \begin{matrix} x={{({{x}_{C}},{{y}_{C}},r)}^{T}} & {} \\ \end{matrix} \\ \end{matrix} \\ \end{matrix} \right.
⎩⎪⎪⎨⎪⎪⎧Δ=Xmin1≤i≤nmax{∣∣Δ(i)(x)∣∣}=Xmin1≤i≤nmax{∣∣∣∣(xP(i)−xC)2+(yP(i)−yC)2−r∣∣∣∣}s.t.r∈(0,+∞)x=(xC,yC,r)T
式中,
n
n
n为给定离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}中离散点的个数,优化变量为任意浮动拟合圆的圆心坐标和半径
x
=
(
R
C
,
r
)
T
=
(
x
C
,
y
C
,
r
)
T
x={{({{R}_{C}},r)}^{T}}={{({{x}_{C}},{{y}_{C}},r)}^{T}}
x=(RC,r)T=(xC,yC,r)T,目标函数为点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}中的点与浮动拟合圆法向误差
∣
Δ
(
i
)
(
x
)
∣
=
∣
(
x
P
(
i
)
−
x
C
)
2
+
(
y
P
(
i
)
−
y
C
)
2
−
r
∣
\left| {{\Delta }^{(i)}}(x) \right|=\left| \sqrt{{{(x_{P}^{(i)}-{{x}_{C}})}^{2}}+{{(y_{P}^{(i)}-{{y}_{C}})}^{2}}}-r \right|
∣∣Δ(i)(x)∣∣=∣∣∣∣(xP(i)−xC)2+(yP(i)−yC)2−r∣∣∣∣,而
Δ
r
r
{{\Delta }_{rr}}
Δrr为鞍圆误差,即目标函数的输出值。
鞍圆具有如下性质∶
- (1)自适应性: 由于采用浮动圆拟合给定点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)},依据点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}的几何形状与分布特点(曲线不变量)自适应确定浮动拟合圆的圆心位置,而且使浮动拟合圆与点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}各点的法向误差中最大值为最小,即
一次鞍点意义,也就是对于每次给定半径的浮动圆拟合都是最恰当位置,拟合误差能够反映当前浮动圆半径的影响,具有自适应性。 - (2)唯一性: 改变浮动圆的半径和位置,在拟合圆参数变化范围内再也没有使得最大法向误差更小的浮动拟合圆,体现
一次极小意义,鞍圆是给定点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}的最佳拟合圆,具有唯一性。所以,运动刚体 Σ ∗ \Sigma * Σ∗上各点 P P P在固定坐标系中的离散点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}都对应于拟合误差最小的唯一鞍圆,只是这些拟合圆的最大拟合误差不同而已,因而鞍圆误差是运动平面上点的坐标的函数。 - (3)可比性: 由于鞍圆误差是最大法向误差,具有统一的度量标准,准确反映了离散点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}与鞍圆的近似程度,对于所有平面运动刚体上点的轨迹与鞍圆的最大法向误差,都是统一评价标准,具有可比性。
该优化模型的求解算法可以直接应用MATLAB软件优化工具箱中的fminimax函数求解,其具体参数设置将在后续算例中进行介绍。初始值对计算量和收敛性有重要影响,在此以最小二乘法计算出离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}的浮动拟合圆为初始值,具有简便高效特点,其解析方程推导过程如下∶
- 当用圆拟合离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}时,令残差为∶
e i = ( x P ( i ) − x C ) 2 + ( y P ( i ) − y C ) 2 − r 2 , i = 1 , 2 , . . . , n {{e}_{i}}={{(x_{P}^{(i)}-{{x}_{C}})}^{2}}+{{(y_{P}^{(i)}-{{y}_{C}})}^{2}}-{{r}^{2}},i=1,2,...,n ei=(xP(i)−xC)2+(yP(i)−yC)2−r2,i=1,2,...,n - 则可得残差的平方和为∶
F = ∑ i = 1 n e i 2 = ∑ i = 1 n [ ( x P ( i ) − x C ) 2 + ( y P ( i ) − y C ) 2 − r 2 ] 2 = ∑ i = 1 n [ ( x P ( i ) ) 2 + ( y P ( i ) ) 2 + A ⋅ x P ( i ) + B ⋅ y P ( i ) + C ] 2 F=\sum\limits_{i=1}^{n}{{{e}_{i}}^{2}}=\sum\limits_{i=1}^{n}{{{[{{(x_{P}^{(i)}-{{x}_{C}})}^{2}}+{{(y_{P}^{(i)}-{{y}_{C}})}^{2}}-{{r}^{2}}]}^{2}}}=\sum\limits_{i=1}^{n}{{{[{{(x_{P}^{(i)})}^{2}}+{{(y_{P}^{(i)})}^{2}}+A\cdot x_{P}^{(i)}+B\cdot y_{P}^{(i)}+C]}^{2}}} F=i=1∑nei2=i=1∑n[(xP(i)−xC)2+(yP(i)−yC)2−r2]2=i=1∑n[(xP(i))2+(yP(i))2+A⋅xP(i)+B⋅yP(i)+C]2
其中: A = − 2 x C , B = − 2 y C , C = x C 2 + y C 2 − r 2 A=-2{{x}_{C}},B=-2{{y}_{C}},C={{x}_{C}}^{2}+{{y}_{C}}^{2}-{{r}^{2}} A=−2xC,B=−2yC,C=xC2+yC2−r2 - 将上式分别对
A
A
A、
B
B
B和
C
C
C求偏导,并令其为零,可得:
{ ∂ F ∂ A = 2 ∑ i = 1 n [ ( x P ( i ) ) 2 + ( y P ( i ) ) 2 + A ⋅ x P ( i ) + B ⋅ y P ( i ) + C ] ⋅ x P ( i ) = 0 ∂ F ∂ B = 2 ∑ i = 1 n [ ( x P ( i ) ) 2 + ( y P ( i ) ) 2 + A ⋅ x P ( i ) + B ⋅ y P ( i ) + C ] ⋅ y P ( i ) = 0 ∂ F ∂ C = 2 ∑ i = 1 n [ ( x P ( i ) ) 2 + ( y P ( i ) ) 2 + A ⋅ x P ( i ) + B ⋅ y P ( i ) + C ] = 0 \left\{ \begin{matrix} \frac{\partial F}{\partial A}=2\sum\limits_{i=1}^{n}{[{{(x_{P}^{(i)})}^{2}}+{{(y_{P}^{(i)})}^{2}}+A\cdot x_{P}^{(i)}+B\cdot y_{P}^{(i)}+C]}\cdot x_{P}^{(i)}=0 \\ \frac{\partial F}{\partial B}=2\sum\limits_{i=1}^{n}{[{{(x_{P}^{(i)})}^{2}}+{{(y_{P}^{(i)})}^{2}}+A\cdot x_{P}^{(i)}+B\cdot y_{P}^{(i)}+C]}\cdot y_{P}^{(i)}=0 \\ \frac{\partial F}{\partial C}=2\sum\limits_{i=1}^{n}{[{{(x_{P}^{(i)})}^{2}}+{{(y_{P}^{(i)})}^{2}}+A\cdot x_{P}^{(i)}+B\cdot y_{P}^{(i)}+C]}=0 \\ \end{matrix} \right. ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧∂A∂F=2i=1∑n[(xP(i))2+(yP(i))2+A⋅xP(i)+B⋅yP(i)+C]⋅xP(i)=0∂B∂F=2i=1∑n[(xP(i))2+(yP(i))2+A⋅xP(i)+B⋅yP(i)+C]⋅yP(i)=0∂C∂F=2i=1∑n[(xP(i))2+(yP(i))2+A⋅xP(i)+B⋅yP(i)+C]=0 - 可得到最小二乘意义下的浮动拟合圆圆心坐标
x
C
{{x}_{C}}
xC、
y
C
{{y}_{C}}
yC和半径
r
r
r为∶
{ x C = c 1 b 2 − c 2 b 1 a 1 b 2 − a 2 b 1 , y C = c 1 a 2 − c 2 a 1 a 1 b 2 − a 2 b 1 r = x C 2 + y C 2 − 2 x C n ∑ i = 1 n x P ( i ) − 2 y C n ∑ i = 1 n y P ( i ) + 1 n [ ∑ i = 1 n ( x P ( i ) ) 2 + ∑ i = 1 n ( y P ( i ) ) 2 ] \left\{ \begin{matrix} {{x}_{C}}=\frac{{{c}_{1}}{{b}_{2}}-{{c}_{2}}{{b}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}},{{y}_{C}}=\frac{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}} \\ r=\sqrt{{{x}_{C}}^{2}+{{y}_{C}}^{2}-2\frac{{{x}_{C}}}{n}\sum\limits_{i=1}^{n}{x_{P}^{(i)}}-2\frac{{{y}_{C}}}{n}\sum\limits_{i=1}^{n}{y_{P}^{(i)}}+\frac{1}{n}[\sum\limits_{i=1}^{n}{{{(x_{P}^{(i)})}^{2}}}+\sum\limits_{i=1}^{n}{{{(y_{P}^{(i)})}^{2}}}]} \\ \end{matrix} \right. ⎩⎪⎨⎪⎧xC=a1b2−a2b1c1b2−c2b1,yC=a1b2−a2b1c1a2−c2a1r=xC2+yC2−2nxCi=1∑nxP(i)−2nyCi=1∑nyP(i)+n1[i=1∑n(xP(i))2+i=1∑n(yP(i))2]
其中:
{ a 1 = 2 ∑ i = 1 n ( x P ( i ) ) 2 − 2 n ( ∑ i = 1 n x P ( i ) ) 2 , b 2 = 2 ∑ i = 1 n ( y P ( i ) ) 2 − 2 n ( ∑ i = 1 n y P ( i ) ) 2 b 1 = a 2 = 2 ∑ i = 1 n x P ( i ) y P ( i ) − 2 n ∑ i = 1 n x P ( i ) ∑ i = 1 n y P ( i ) c 1 = ∑ i = 1 n ( x P ( i ) ) 3 + ∑ i = 1 n x P ( i ) ( y P ( i ) ) 2 − 1 n ∑ i = 1 n x P ( i ) [ ∑ i = 1 n ( x P ( i ) ) 2 + ∑ i = 1 n ( y P ( i ) ) 2 ] c 2 = ∑ i = 1 n ( y P ( i ) ) 3 + ∑ i = 1 n y P ( i ) ( x P ( i ) ) 2 − 1 n ∑ i = 1 n y P ( i ) [ ∑ i = 1 n ( x P ( i ) ) 2 + ∑ i = 1 n ( y P ( i ) ) 2 ] \left\{ \begin{matrix} {{a}_{1}}=2\sum\limits_{i=1}^{n}{{{(x_{P}^{(i)})}^{2}}}-\frac{2}{n}{{(\sum\limits_{i=1}^{n}{x_{P}^{(i)}})}^{2}},{{b}_{2}}=2\sum\limits_{i=1}^{n}{{{(y_{P}^{(i)})}^{2}}}-\frac{2}{n}{{(\sum\limits_{i=1}^{n}{y_{P}^{(i)}})}^{2}} \\ {{b}_{1}}={{a}_{2}}=2\sum\limits_{i=1}^{n}{x_{P}^{(i)}y_{P}^{(i)}}-\frac{2}{n}\sum\limits_{i=1}^{n}{x_{P}^{(i)}}\sum\limits_{i=1}^{n}{y_{P}^{(i)}} \\ {{c}_{1}}=\sum\limits_{i=1}^{n}{{{(x_{P}^{(i)})}^{3}}}+\sum\limits_{i=1}^{n}{x_{P}^{(i)}{{(y_{P}^{(i)})}^{2}}}-\frac{1}{n}\sum\limits_{i=1}^{n}{x_{P}^{(i)}[\sum\limits_{i=1}^{n}{{{(x_{P}^{(i)})}^{2}}}+\sum\limits_{i=1}^{n}{{{(y_{P}^{(i)})}^{2}}}]} \\ {{c}_{2}}=\sum\limits_{i=1}^{n}{{{(y_{P}^{(i)})}^{3}}}+\sum\limits_{i=1}^{n}{y_{P}^{(i)}{{(x_{P}^{(i)})}^{2}}}-\frac{1}{n}\sum\limits_{i=1}^{n}{y_{P}^{(i)}[\sum\limits_{i=1}^{n}{{{(x_{P}^{(i)})}^{2}}}+\sum\limits_{i=1}^{n}{{{(y_{P}^{(i)})}^{2}}}]} \\ \end{matrix} \right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧a1=2i=1∑n(xP(i))2−n2(i=1∑nxP(i))2,b2=2i=1∑n(yP(i))2−n2(i=1∑nyP(i))2b1=a2=2i=1∑nxP(i)yP(i)−n2i=1∑nxP(i)i=1∑nyP(i)c1=i=1∑n(xP(i))3+i=1∑nxP(i)(yP(i))2−n1i=1∑nxP(i)[i=1∑n(xP(i))2+i=1∑n(yP(i))2]c2=i=1∑n(yP(i))3+i=1∑nyP(i)(xP(i))2−n1i=1∑nyP(i)[i=1∑n(xP(i))2+i=1∑n(yP(i))2]
可根据鞍圆优化模型,直接采用MATLAB软件优化工具箱中的fminimax函数通过如下设置求解∶
[x,fval] = fminimax(fun, x0, A, b, Aeq, beq, lb, ub, nonlcon, options)
优化函数
fminimax的设置(options)定为默认设置,该函数的左端为输出,即∶
x∶为最优解,即离散轨迹点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}, i = 1 , . . , n i=1,..,n i=1,..,n的鞍圆参数,包括圆心坐标 x C {{x}_{C}} xC, y C {{y}_{C}} yC及半径 r r r。
fval∶为目标函数值,即离散轨迹点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}, i = 1 , . . , n i=1,..,n i=1,..,n对应的鞍圆误差。
优化函数fminimax的右端为输入,分别有∶
fun∶为目标函数,即离散轨迹点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}, i = 1 , . . , n i=1,..,n i=1,..,n与任意浮动拟合圆的法向误差,即 { ∣ ( x P ( i ) − x C ) 2 + ( y P ( i ) − y C ) 2 − r ∣ } , i = 1 , . . , n \{\left| \sqrt{{{(x_{P}^{(i)}-{{x}_{C}})}^{2}}+{{(y_{P}^{(i)}-{{y}_{C}})}^{2}}}-r \right|\},i=1,..,n {∣∣∣∣(xP(i)−xC)2+(yP(i)−yC)2−r∣∣∣∣},i=1,..,n。
x0∶为初始值,即优化变量(拟合圆的圆心坐标以及半径)的初始值,按照最小二乘法确定,并由上式计算得到其具体值。
A,b,Aeq,beq,lb,ub,nonlcon∶优化约束与变量上、下界,线性约束A,b,Aeq,beq和非线性约束nonlcon均设置为空,优化变量的下界lb= [-Inf,-Inf,0],优化变量的上界ub=[Inf,Inf,Inf]。
依据上述参数设置,可以将离散点集的鞍圆拟合编制成子函数(ArrF),该子函数的输入为离散点集中各点的坐标,输出为鞍圆的圆心坐标、半径以及鞍圆误差
Δ
r
r
{{\Delta }_{rr}}
Δrr,形成鞍圆拟合子程序ArrF。
2.3.2 鞍圆误差
为讨论曲线鞍圆拟合的误差性质,在此先假定运动刚体平面上点P在固定坐标系
{
O
f
;
i
⃗
f
,
j
⃗
f
}
\{{{O}_{f}};{{{\vec{i}}}_{f}},{{{\vec{j}}}_{f}}\}
{Of;if,jf}中的轨迹
Γ
P
{{\Gamma }_{P}}
ΓP为连续曲线,在定义2.1中按最大法向拟合误差最小为原则确定唯一的鞍圆,其拟合误差
Δ
r
r
{{\Delta }_{rr}}
Δrr,对于曲线
Γ
P
{{\Gamma }_{P}}
ΓP上所有点而言,是最大误差(全局极大值),而对于所有拟合圆参数
(
x
C
,
y
C
,
r
)
({{x}_{C}},{{y}_{C}},r)
(xC,yC,r)而言,该最大误差值又是最小的(全局极小值)。
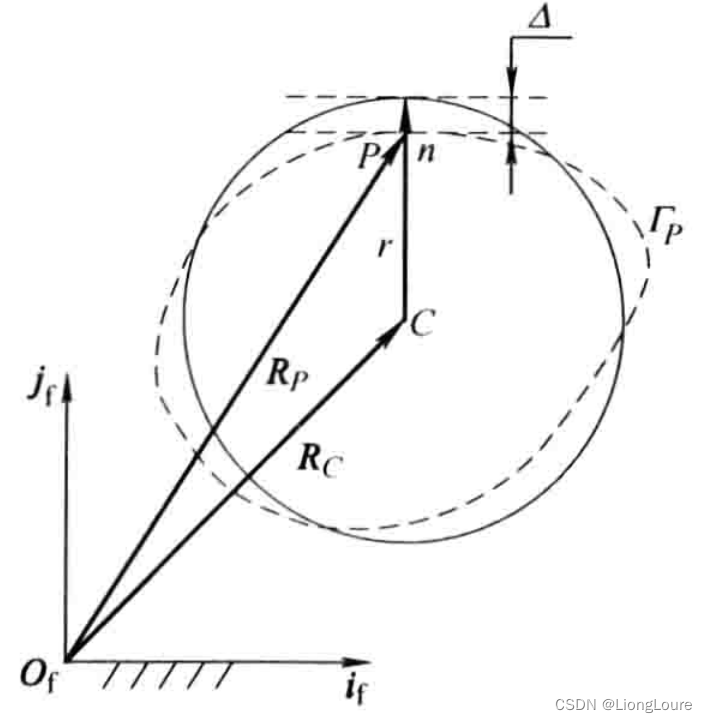
对于给定曲线
Γ
P
{{\Gamma }_{P}}
ΓP上任意点
P
P
P对应鞍圆上相应点及法向误差
Δ
r
r
{{\Delta }_{rr}}
Δrr,其矢量方程
R
⃗
P
{{{\vec{R}}}_{P}}
RP可写为∶
R
⃗
P
=
R
⃗
C
+
(
r
+
Δ
)
n
⃗
{{{\vec{R}}}_{P}}\text{=}{{{\vec{R}}}_{C}}+(r+\Delta )\vec{n}
RP=RC+(r+Δ)n
R
⃗
C
{{{\vec{R}}}_{C}}
RC为鞍圆圆心矢径,
r
r
r为鞍圆半径(正数),而鞍圆在点
P
P
P对应点处的单位法矢为
n
⃗
{\vec{n}}
n,法向误差
Δ
\Delta
Δ正负号依据点
P
P
P在鞍圆内外而定(外面取“+”,里面取“-”)。可得到曲线
Γ
P
{{\Gamma }_{P}}
ΓP上任意点处的拟合误差
Δ
\Delta
Δ为∶
Δ
=
(
R
⃗
P
−
R
⃗
C
)
⋅
n
⃗
−
r
\Delta =({{{\vec{R}}}_{P}}-{{{\vec{R}}}_{C}})\cdot \vec{n}-r
Δ=(RP−RC)⋅n−r
对于给定曲线
Γ
P
{{\Gamma }_{P}}
ΓP,对应的一个确定鞍圆,
r
r
r为常数而且
R
⃗
C
{{{\vec{R}}}_{C}}
RC为常矢量,将误差函数对 曲线
Γ
P
{{\Gamma }_{P}}
ΓP的弧长
s
s
s 求导,有∶
d
Δ
d
s
=
d
R
⃗
P
d
s
⋅
n
⃗
+
(
R
⃗
P
−
R
⃗
C
)
⋅
d
n
⃗
d
s
\frac{d\Delta }{ds}=\frac{d{{{\vec{R}}}_{P}}}{ds}\cdot \vec{n}+({{{\vec{R}}}_{P}}-{{{\vec{R}}}_{C}})\cdot \frac{d\vec{n}}{ds}
dsdΔ=dsdRP⋅n+(RP−RC)⋅dsdn
且知:
R
⃗
P
−
R
⃗
C
=
(
r
+
Δ
)
n
⃗
{{{\vec{R}}}_{P}}-{{{\vec{R}}}_{C}}=(r+\Delta )\vec{n}
RP−RC=(r+Δ)n,则
(
R
⃗
P
−
R
⃗
C
)
⋅
d
n
⃗
d
s
=
(
r
+
Δ
)
n
⃗
⋅
d
n
⃗
d
s
=
0
({{{\vec{R}}}_{P}}-{{{\vec{R}}}_{C}})\cdot \frac{d\vec{n}}{ds}=(r+\Delta )\vec{n}\cdot \frac{d\vec{n}}{ds}=0
(RP−RC)⋅dsdn=(r+Δ)n⋅dsdn=0,在曲线
Γ
P
{{\Gamma }_{P}}
ΓP上点
P
P
P处误差
Δ
\Delta
Δ取得极值条件
d
Δ
d
s
=
0
\frac{d\Delta }{ds}=0
dsdΔ=0,得:
d
R
⃗
P
d
s
⋅
n
⃗
=
0
\frac{d{{{\vec{R}}}_{P}}}{ds}\cdot \vec{n}=0
dsdRP⋅n=0
∣ n ⃗ ∣ 2 = 1 ⇒ d ∣ n ⃗ ∣ 2 d s = 0 ⇒ 2 n ⃗ ⋅ d n ⃗ d s = 0 |\vec{n}{{|}^{2}}=1\Rightarrow \frac{d|\vec{n}{{|}^{2}}}{ds}=0\Rightarrow 2\vec{n}\cdot \frac{d\vec{n}}{ds}=0 ∣n∣2=1⇒dsd∣n∣2=0⇒2n⋅dsdn=0
上式说明曲线
Γ
P
{{\Gamma }_{P}}
ΓP在
P
P
P点的切线
d
R
⃗
P
d
s
\frac{d{{{\vec{R}}}_{P}}}{ds}
dsdRP与鞍圆法线n正交时,曲线
Γ
P
{{\Gamma }_{P}}
ΓP在P点的法线与鞍圆法线重合,法向误差
Δ
\Delta
Δ取得极值。在曲线
Γ
P
{{\Gamma }_{P}}
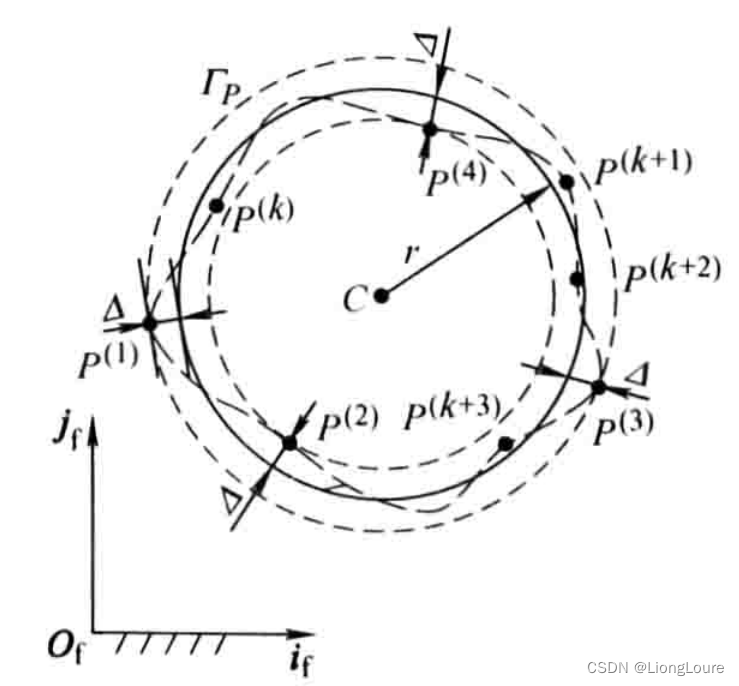
ΓP上可能存在有多点处的法线通过圆心,其误差取得极值,但不一定是最大值,如下图所示的
P
(
k
+
1
)
{{P}^{(k+1)}}
P(k+1),
P
(
k
+
2
)
{{P}^{(k+2)}}
P(k+2)和
P
(
k
+
3
)
{{P}^{(k+3)}}
P(k+3)点,只有法向误差绝对值的最大值才为鞍圆误差
Δ
r
r
{{\Delta }_{rr}}
Δrr。
按平面曲线右手系约定,将曲线
Γ
P
{{\Gamma }_{P}}
ΓP在其上任意点的法线表示为
d
R
⃗
P
d
s
×
k
⃗
\frac{d{{{\vec{R}}}_{P}}}{ds}\times \vec{k}
dsdRP×k,那么,在曲线
Γ
P
{{\Gamma }_{P}}
ΓP上拟合误差
Δ
\Delta
Δ取得极值的点处,鞍圆圆心矢量可表示为:
R
⃗
C
=
R
⃗
P
−
(
r
+
Δ
)
d
R
⃗
P
d
s
×
k
⃗
{{{\vec{R}}}_{C}}={{{\vec{R}}}_{P}}-(r+\Delta )\frac{d{{{\vec{R}}}_{P}}}{ds}\times \vec{k}
RC=RP−(r+Δ)dsdRP×k
对于给定曲线
Γ
P
{{\Gamma }_{P}}
ΓP,要确定鞍圆三个参数
(
x
C
,
y
C
,
r
)
({{x}_{C}},{{y}_{C}},r)
(xC,yC,r)和鞍圆误差
Δ
\Delta
Δ,至少需要有四个点使得
d
R
⃗
P
d
s
⋅
n
⃗
=
0
\frac{d{{{\vec{R}}}_{P}}}{ds}\cdot \vec{n}=0
dsdRP⋅n=0成立(需判断最大值),求得各点处的
d
R
⃗
P
d
s
\frac{d{{{\vec{R}}}_{P}}}{ds}
dsdRP代入
R
⃗
C
=
R
⃗
P
−
(
r
+
Δ
)
d
R
⃗
P
d
s
×
k
⃗
{{{\vec{R}}}_{C}}={{{\vec{R}}}_{P}}-(r+\Delta )\frac{d{{{\vec{R}}}_{P}}}{ds}\times \vec{k}
RC=RP−(r+Δ)dsdRP×k,联立解出
(
x
C
,
y
C
,
r
)
({{x}_{C}},{{y}_{C}},r)
(xC,yC,r)和
Δ
r
r
{{\Delta }_{rr}}
Δrr,多于四点为冗余情况。
鞍点规划理论已经证明:对于一条非退化的平面曲线,以鞍点规划模型(最大误差最小)确定的拟合圆,曲线上至少有四点处的误差取得相同最大值(必为极大值),且分布在拟合圆的内部和外部各两点。
这一理论应用于评定圆度误差时,相当于采用两个同心圆包容被拟合曲线,内外圆与被包容曲线的切点即为最大误差点。
由此可见,以鞍点规划(最大误差最小)模型定义平面曲线的鞍圆时,被拟合曲线上的四个特征点确定了鞍圆的位置、半径和误差,称为鞍圆拟合特征点,分布在鞍圆的内外两侧各两个,该点处的误差即为鞍圆误差。如例2-1,对于给定的拟合曲线——椭圆,只要长轴上两顶点和短轴上两顶点(四个拟合特征点)确定,鞍圆及其误差便随之而定。当鞍圆误差趋于零时,被拟合曲线趋近于圆。
当被拟合曲线
Γ
P
{{\Gamma }_{P}}
ΓP为离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}时
Γ
P
{{\Gamma }_{P}}
ΓP上任意点与鞍圆的误差
Δ
(
i
)
{{\Delta }^{(i)}}
Δ(i)由
Δ
=
(
R
⃗
P
−
R
⃗
C
)
⋅
n
⃗
−
r
\Delta =({{{\vec{R}}}_{P}}-{{{\vec{R}}}_{C}})\cdot \vec{n}-r
Δ=(RP−RC)⋅n−r改写为离散形式∶
Δ
(
i
)
=
∣
R
⃗
P
(
i
)
−
R
⃗
C
∣
−
r
=
(
x
P
(
i
)
−
x
C
)
2
+
(
y
P
(
i
)
−
y
C
)
2
−
r
,
R
⃗
P
(
i
)
=
[
M
(
i
)
]
⋅
R
⃗
P
m
{{\Delta }^{(i)}}=\left| \vec{R}_{P}^{(i)}-{{{\vec{R}}}_{C}} \right|-r=\sqrt{{{(x_{P}^{(i)}-{{x}_{C}})}^{2}}+{{(y_{P}^{(i)}-{{y}_{C}})}^{2}}}-r,\vec{R}_{P}^{(i)}=[{{M}^{(i)}}]\cdot {{{\vec{R}}}_{Pm}}
Δ(i)=∣∣∣RP(i)−RC∣∣∣−r=(xP(i)−xC)2+(yP(i)−yC)2−r,RP(i)=[M(i)]⋅RPm
而鞍圆误差为其中的最大值,其计算公式为∶
Δ
r
r
=
max
{
∣
Δ
(
i
)
∣
}
=
max
{
∣
(
x
P
(
i
)
−
x
C
)
2
+
(
y
P
(
i
)
−
y
C
)
2
−
r
∣
}
{{\Delta }_{rr}}=\max \{\left| {{\Delta }^{(i)}} \right|\}=\max \{\left| \sqrt{{{(x_{P}^{(i)}-{{x}_{C}})}^{2}}+{{(y_{P}^{(i)}-{{y}_{C}})}^{2}}}-r \right|\}
Δrr=max{∣∣∣Δ(i)∣∣∣}=max{∣∣∣∣(xP(i)−xC)2+(yP(i)−yC)2−r∣∣∣∣}
那么,连续曲线的法向误差计算由离散计算替代,离散点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}中的鞍圆拟合特征点由上式通过数值计算和比较产生。
由此可知,离散运动刚体上一点在固定平面坐标系中产生一离散点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)},该点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}中的四个鞍圆拟合特征点确定唯一鞍圆,四个鞍圆拟合特征点所对应运动刚体的离散位置,称为鞍圆拟合特征位置。显然,鞍点规划模型建立了离散运动(鞍圆拟合特征位置)、运动刚体上点、离散轨迹(鞍圆拟合特征点)、鞍圆(位置)和鞍圆误差的相互对应关系,为讨论离散点集 { R P ( i ) } \{R_{P}^{(i)}\} {RP(i)}与圆比较的整体几何性质提供了依据。
2.3.3 四位置鞍圆
当离散运动刚体在固定坐标系中仅有四个位置时,位置分别编号为1、2、3、4,运动刚体上任意点P对应离散轨迹点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)},
i
=
1
,
2
,
3
,
4
i=1,2,3,4
i=1,2,3,4。依据鞍圆拟合模型,调用鞍圆拟合子程序ArrF,得到对应的鞍圆,称为四位置鞍圆。点集
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)}中四个离散点都是鞍圆拟合特征点,分别以
P
(
1
)
,
P
(
2
)
,
P
(
3
)
,
P
(
4
)
{{P}^{(1)}},{{P}^{(2)}},{{P}^{(3)}},{{P}^{(4)}}
P(1),P(2),P(3),P(4)表示,分布在鞍圆内部和外部各两个,运动刚体的四个位置都是鞍圆拟合特征位置。
为便于讨论鞍圆性质,先讨论四位置鞍圆误差的代数方程。由
Δ
(
i
)
=
∣
R
⃗
P
(
i
)
−
R
⃗
C
∣
−
r
=
(
x
P
(
i
)
−
x
C
)
2
+
(
y
P
(
i
)
−
y
C
)
2
−
r
,
R
⃗
P
(
i
)
=
[
M
(
i
)
]
⋅
R
⃗
P
m
{{\Delta }^{(i)}}=\left| \vec{R}_{P}^{(i)}-{{{\vec{R}}}_{C}} \right|-r=\sqrt{{{(x_{P}^{(i)}-{{x}_{C}})}^{2}}+{{(y_{P}^{(i)}-{{y}_{C}})}^{2}}}-r,\vec{R}_{P}^{(i)}=[{{M}^{(i)}}]\cdot {{{\vec{R}}}_{Pm}}
Δ(i)=∣∣∣RP(i)−RC∣∣∣−r=(xP(i)−xC)2+(yP(i)−yC)2−r,RP(i)=[M(i)]⋅RPm写出四个位置的鞍圆误差方程∶
(
r
±
Δ
)
2
=
(
R
⃗
P
(
i
)
−
R
⃗
C
)
2
,
R
⃗
P
(
i
)
=
[
M
(
i
)
]
⋅
R
⃗
P
m
,
i
=
1
,
2
,
3
,
4
{{(r\pm \Delta )}^{2}}={{(\vec{R}_{P}^{(i)}-{{{\vec{R}}}_{C}})}^{2}},\vec{R}_{P}^{(i)}=[{{M}^{(i)}}]\cdot {{{\vec{R}}}_{Pm}},i=1,2,3,4
(r±Δ)2=(RP(i)−RC)2,RP(i)=[M(i)]⋅RPm,i=1,2,3,4
对于给定四个离散位置,依据鞍点规划理论,鞍圆误差为最大拟合误差(极大值)最小,而且拟合特征点
P
(
1
)
,
P
(
2
)
,
P
(
3
)
,
P
(
4
)
{{P}^{(1)}},{{P}^{(2)}},{{P}^{(3)}},{{P}^{(4)}}
P(1),P(2),P(3),P(4)两两分布在拟合圆的内部和外部,因而对于上式,当
i
i
i任取位置编号中的任意两个时,
Δ
\Delta
Δ前符号取正,而当
i
i
i取另两个编号时,符号取负。 令四个拟合特征点处的误差相等(实现两两分布),并使得最大拟合误差取得极小值(不一定是最小值)的拟合圆,称为分布圆。 只可能有三种分布情况,对应三个分布圆,如点
P
(
1
)
{{P}^{(1)}}
P(1)和
P
(
2
)
{{P}^{(2)}}
P(2)在拟合圆内部时,表示为
P
(
1
)
P
(
2
)
−
P
(
3
)
P
(
4
)
{{P}^{(1)}}{{P}^{(2)}}-{{P}^{(3)}}{{P}^{(4)}}
P(1)P(2)−P(3)P(4),同理有
P
(
1
)
P
(
3
)
−
P
(
2
)
P
(
4
)
{{P}^{(1)}}{{P}^{(3)}}-{{P}^{(2)}}{{P}^{(4)}}
P(1)P(3)−P(2)P(4),
P
(
1
)
P
(
4
)
−
P
(
2
)
P
(
3
)
{{P}^{(1)}}{{P}^{(4)}}-{{P}^{(2)}}{{P}^{(3)}}
P(1)P(4)−P(2)P(3),如下图所示:
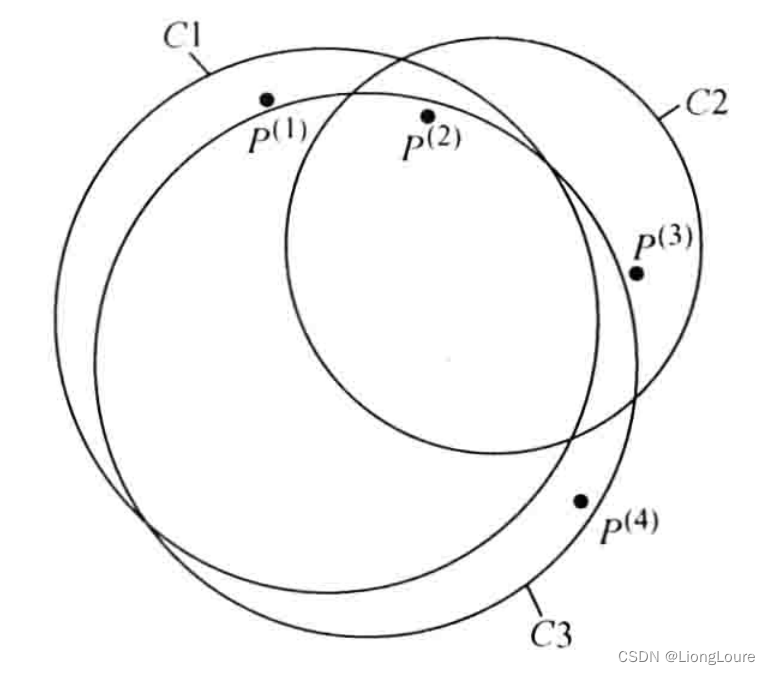
只有三种分布圆: 对于四个点而言都是鞍圆拟合的特征位置,而为了确定鞍圆的圆心,任选两个点为内/外同心圆上两点,其余两点为外/内同心圆上两点;对于不同的选择组合会产生不同中垂线的交点,而内外本身根据中垂线的长度进行区分,与最开始规划无关。
对于
P
(
1
)
P
(
2
)
−
P
(
3
)
P
(
4
)
{{P}^{(1)}}{{P}^{(2)}}-{{P}^{(3)}}{{P}^{(4)}}
P(1)P(2)−P(3)P(4)情况,分布圆的圆心
C
C
C为线段
P
(
1
)
P
(
2
)
{{P}^{(1)}}{{P}^{(2)}}
P(1)P(2)中垂线和
P
(
3
)
P
(
4
)
{{P}^{(3)}}{{P}^{(4)}}
P(3)P(4)中垂线的交点,其在固定坐标系中的坐标为∶
{
y
C
=
[
(
x
P
(
4
)
)
2
+
(
y
P
(
4
)
)
2
−
(
x
P
(
3
)
)
2
−
(
y
P
(
3
)
)
2
]
(
x
P
(
2
)
−
x
P
(
1
)
)
−
[
(
x
P
(
2
)
)
2
+
(
y
P
(
2
)
)
2
−
(
x
P
(
1
)
)
2
−
(
y
P
(
1
)
)
2
]
(
x
P
(
4
)
−
x
P
(
3
)
)
2
(
x
P
(
2
)
−
x
P
(
1
)
)
(
y
P
(
4
)
−
y
P
(
3
)
)
−
2
(
x
P
(
4
)
−
x
P
(
3
)
)
(
y
P
(
2
)
−
y
P
(
1
)
)
x
C
=
[
(
x
P
(
4
)
)
2
+
(
y
P
(
4
)
)
2
−
(
x
P
(
3
)
)
2
−
(
y
P
(
3
)
)
2
]
(
y
P
(
2
)
−
y
P
(
1
)
)
−
[
(
x
P
(
2
)
)
2
+
(
y
P
(
2
)
)
2
−
(
x
P
(
1
)
)
2
−
(
y
P
(
1
)
)
2
]
(
y
P
(
4
)
−
y
P
(
3
)
)
2
(
y
P
(
2
)
−
y
P
(
1
)
)
(
x
P
(
4
)
−
x
P
(
3
)
)
−
2
(
y
P
(
4
)
−
y
P
(
3
)
)
(
x
P
(
2
)
−
x
P
(
1
)
)
\left\{ \begin{matrix} {{y}_{C}}=\frac{[{{(x_{P}^{(4)})}^{2}}+{{(y_{P}^{(4)})}^{2}}-{{(x_{P}^{(3)})}^{2}}-{{(y_{P}^{(3)})}^{2}}](x_{P}^{(2)}-x_{P}^{(1)})-[{{(x_{P}^{(2)})}^{2}}+{{(y_{P}^{(2)})}^{2}}-{{(x_{P}^{(1)})}^{2}}-{{(y_{P}^{(1)})}^{2}}](x_{P}^{(4)}-x_{P}^{(3)})}{2(x_{P}^{(2)}-x_{P}^{(1)})(y_{P}^{(4)}-y_{P}^{(3)})-2(x_{P}^{(4)}-x_{P}^{(3)})(y_{P}^{(2)}-y_{P}^{(1)})} \\ {{x}_{C}}=\frac{[{{(x_{P}^{(4)})}^{2}}+{{(y_{P}^{(4)})}^{2}}-{{(x_{P}^{(3)})}^{2}}-{{(y_{P}^{(3)})}^{2}}](y_{P}^{(2)}-y_{P}^{(1)})-[{{(x_{P}^{(2)})}^{2}}+{{(y_{P}^{(2)})}^{2}}-{{(x_{P}^{(1)})}^{2}}-{{(y_{P}^{(1)})}^{2}}](y_{P}^{(4)}-y_{P}^{(3)})}{2(y_{P}^{(2)}-y_{P}^{(1)})(x_{P}^{(4)}-x_{P}^{(3)})-2(y_{P}^{(4)}-y_{P}^{(3)})(x_{P}^{(2)}-x_{P}^{(1)})} \\ \end{matrix} \right.
⎩⎪⎨⎪⎧yC=2(xP(2)−xP(1))(yP(4)−yP(3))−2(xP(4)−xP(3))(yP(2)−yP(1))[(xP(4))2+(yP(4))2−(xP(3))2−(yP(3))2](xP(2)−xP(1))−[(xP(2))2+(yP(2))2−(xP(1))2−(yP(1))2](xP(4)−xP(3))xC=2(yP(2)−yP(1))(xP(4)−xP(3))−2(yP(4)−yP(3))(xP(2)−xP(1))[(xP(4))2+(yP(4))2−(xP(3))2−(yP(3))2](yP(2)−yP(1))−[(xP(2))2+(yP(2))2−(xP(1))2−(yP(1))2](yP(4)−yP(3))
由圆心点
C
C
C、分布圆内点
P
(
1
)
{{P}^{(1)}}
P(1)和分布圆外点
P
(
3
)
{{P}^{(3)}}
P(3)的三点坐标得到
P
(
1
)
P
(
2
)
−
P
(
3
)
P
(
4
)
{{P}^{(1)}}{{P}^{(2)}}-{{P}^{(3)}}{{P}^{(4)}}
P(1)P(2)−P(3)P(4)情况下的分布圆误差
Δ
12
,
34
{{\Delta }_{12,34}}
Δ12,34为∶
Δ
12
,
34
=
∣
(
x
P
(
1
)
−
x
C
)
2
+
(
y
P
(
1
)
−
y
C
)
2
−
(
x
P
(
3
)
−
x
C
)
2
+
(
y
P
(
3
)
−
y
C
)
2
∣
2
{{\Delta }_{12,34}}=\frac{\left| \sqrt{{{(x_{P}^{(1)}-{{x}_{C}})}^{2}}+{{(y_{P}^{(1)}-{{y}_{C}})}^{2}}}-\sqrt{{{(x_{P}^{(3)}-{{x}_{C}})}^{2}}+{{(y_{P}^{(3)}-{{y}_{C}})}^{2}}} \right|}{2}
Δ12,34=2∣∣∣∣(xP(1)−xC)2+(yP(1)−yC)2−(xP(3)−xC)2+(yP(3)−yC)2∣∣∣∣
将的
x
C
{{x}_{C}}
xC和
y
C
{{y}_{C}}
yC代入上式并展开可得∶
16
Δ
12
,
34
4
−
8
Δ
12
,
34
2
[
(
x
P
(
1
)
−
x
C
)
2
+
(
y
P
(
1
)
−
y
C
)
)
2
−
(
x
P
(
3
)
−
x
C
)
2
−
(
y
P
(
3
)
−
y
C
)
2
]
+
[
(
x
P
(
1
)
−
x
C
)
2
+
(
y
P
(
1
)
−
y
C
)
)
2
−
(
x
P
(
3
)
−
x
C
)
2
−
(
y
P
(
3
)
−
y
C
)
2
]
2
=
0
16{{\Delta }_{12,34}}^{4}-8{{\Delta }_{12,34}}^{2}{{[{{(x_{P}^{(1)}-{{x}_{C}})}^{2}}+(y_{P}^{(1)}-{{y}_{C}}))}^{2}}-{{(x_{P}^{(3)}-{{x}_{C}})}^{2}}-{{(y_{P}^{(3)}-{{y}_{C}})}^{2}}]+{{[{{(x_{P}^{(1)}-{{x}_{C}})}^{2}}+(y_{P}^{(1)}-{{y}_{C}}))}^{2}}-{{(x_{P}^{(3)}-{{x}_{C}})}^{2}}-{{(y_{P}^{(3)}-{{y}_{C}})}^{2}}{{]}^{2}}=0
16Δ12,344−8Δ12,342[(xP(1)−xC)2+(yP(1)−yC))2−(xP(3)−xC)2−(yP(3)−yC)2]+[(xP(1)−xC)2+(yP(1)−yC))2−(xP(3)−xC)2−(yP(3)−yC)2]2=0
将
[
x
P
(
i
)
y
P
(
i
)
1
]
=
[
M
(
i
)
]
[
x
P
m
y
P
m
1
]
,
[
M
(
i
)
]
=
[
cos
γ
(
i
)
−
sin
γ
(
i
)
x
O
m
f
(
i
)
sin
γ
(
i
)
cos
γ
(
i
)
y
O
m
f
(
i
)
0
0
1
]
\left[ \begin{matrix} x_{P}^{(i)} \\ y_{P}^{(i)} \\ 1 \\ \end{matrix} \right]=[{{M}^{(i)}}]\left[ \begin{matrix} {{x}_{Pm}} \\ {{y}_{Pm}} \\ 1 \\ \end{matrix} \right],[{{M}^{(i)}}]=\left[ \begin{matrix} \cos {{\gamma }^{(i)}} & -\sin {{\gamma }^{(i)}} & x_{Omf}^{(i)} \\ \sin {{\gamma }^{(i)}} & \cos {{\gamma }^{(i)}} & y_{Omf}^{(i)} \\ 0 & 0 & 1 \\ \end{matrix} \right]
⎣⎢⎡xP(i)yP(i)1⎦⎥⎤=[M(i)]⎣⎡xPmyPm1⎦⎤,[M(i)]=⎣⎢⎡cosγ(i)sinγ(i)0−sinγ(i)cosγ(i)0xOmf(i)yOmf(i)1⎦⎥⎤坐标变换代入式(2.25b),化简可得关于
x
P
m
,
y
P
m
,
Δ
12
,
34
{{x}_{Pm}},{{y}_{Pm}},{{\Delta }_{12,34}}
xPm,yPm,Δ12,34的十二次代数方程。同理,可得到
P
(
1
)
P
(
3
)
−
P
(
2
)
P
(
4
)
{{P}^{(1)}}{{P}^{(3)}}-{{P}^{(2)}}{{P}^{(4)}}
P(1)P(3)−P(2)P(4)情况下分布圆误差
Δ
13
,
24
{{\Delta }_{13,24}}
Δ13,24以及
P
(
1
)
P
(
4
)
−
P
(
2
)
P
(
3
)
{{P}^{(1)}}{{P}^{(4)}}-{{P}^{(2)}}{{P}^{(3)}}
P(1)P(4)−P(2)P(3)情况下的分布圆误差
Δ
14
,
23
{{\Delta }_{14,23}}
Δ14,23。则四位置鞍圆误差
Δ
1234
{{\Delta }_{1234}}
Δ1234为3个分布圆误差的最小值∶
Δ
1234
=
min
(
Δ
12
,
34
,
Δ
13
,
24
,
Δ
14
,
23
)
{{\Delta }_{1234}}=\min ({{\Delta }_{12,34}},{{\Delta }_{13,24}},{{\Delta }_{14,23}})
Δ1234=min(Δ12,34,Δ13,24,Δ14,23)
也可以写成如下形式:
Δ
1234
=
1
2
∣
∣
∣
Δ
12
,
34
+
Δ
13
,
24
∣
2
−
∣
Δ
12
,
34
−
Δ
13
,
24
∣
2
∣
+
Δ
14
,
23
∣
−
1
2
∣
∣
∣
Δ
12
,
34
+
Δ
13
,
24
∣
2
−
∣
Δ
12
,
34
−
Δ
13
,
24
∣
2
∣
−
Δ
14
,
23
∣
{{\Delta }_{1234}}=\frac{1}{2}\left| \left| \frac{\left| {{\Delta }_{12,34}}+{{\Delta }_{13,24}} \right|}{2}-\frac{\left| {{\Delta }_{12,34}}-{{\Delta }_{13,24}} \right|}{2} \right|+{{\Delta }_{14,23}} \right|-\frac{1}{2}\left| \left| \frac{\left| {{\Delta }_{12,34}}+{{\Delta }_{13,24}} \right|}{2}-\frac{\left| {{\Delta }_{12,34}}-{{\Delta }_{13,24}} \right|}{2} \right|-{{\Delta }_{14,23}} \right|
Δ1234=21∣∣∣∣∣∣2∣Δ12,34+Δ13,24∣−2∣Δ12,34−Δ13,24∣∣∣∣+Δ14,23∣∣∣−21∣∣∣∣∣∣2∣Δ12,34+Δ13,24∣−2∣Δ12,34−Δ13,24∣∣∣∣−Δ14,23∣∣∣
四位置鞍圆误差曲面为分片十二次代数曲面。
以运动刚体上点坐标
(
x
P
m
,
y
P
m
)
({{x}_{Pm}},{{y}_{Pm}})
(xPm,yPm)为自变量,其轨迹离散点集的四位置鞍圆误差
Δ
1234
{{\Delta }_{1234}}
Δ1234为因变量,构造出四位置运动刚体上点-鞍圆误差曲面,并把对应相同误差值的点以曲线连接成为等高线,如下图所示:
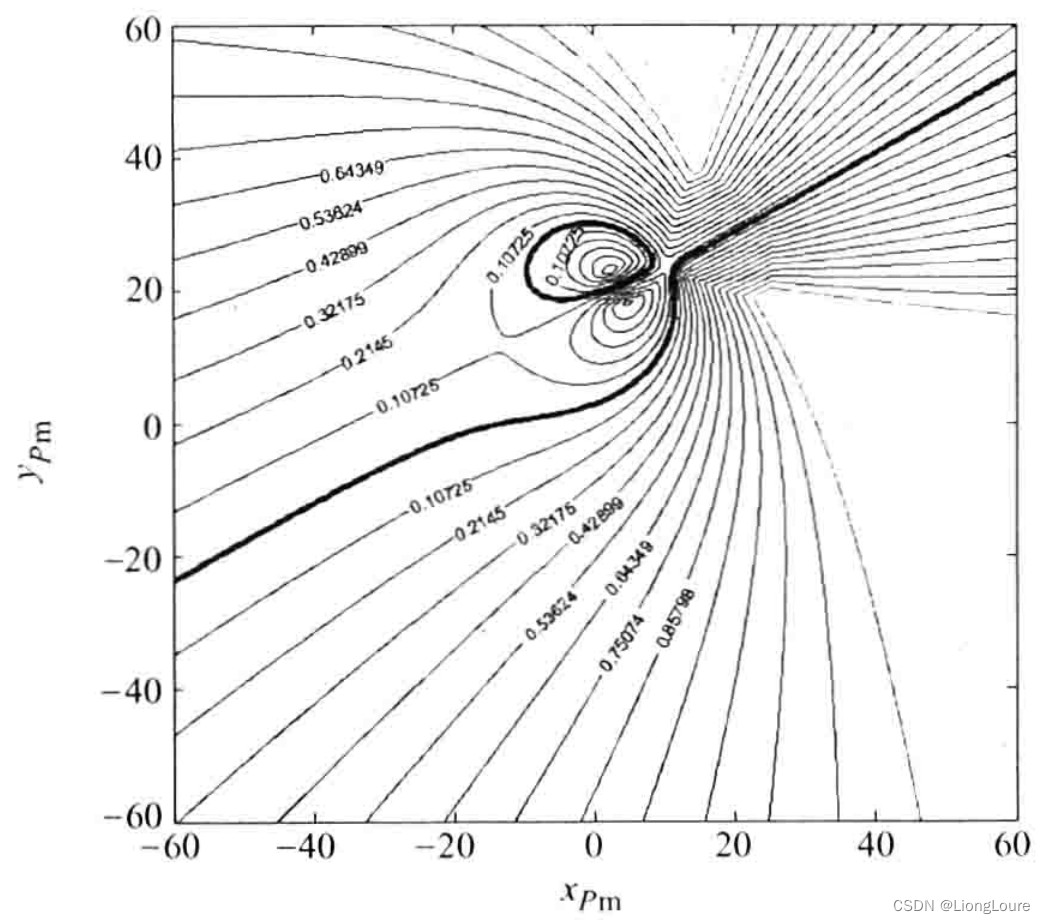
当鞍圆误差值
Δ
=
0
\Delta =0
Δ=0时,相当于该误差曲面被
Δ
=
0
\Delta =0
Δ=0的平面所截得曲线——圆点曲线,恰为误差曲面的谷底,图中所示粗实线为圆点曲线。数据来自表2.1给出的平面运动刚体十个离散位置中的前四个离散位置。
2.3.4 五位置鞍圆
给定运动刚体五个离散位置,其位置编号为1、2、3、4、5,运动刚体上任意点
P
P
P在固定坐标系中产生离散轨迹
{
R
P
(
i
)
}
\{R_{P}^{(i)}\}
{RP(i)},
i
=
1
,
2
,
3
,
4
,
5
i=1,2,3,4,5
i=1,2,3,4,5,依据鞍圆拟合模型,调用鞍圆拟合子程序ArrF,得到该离散轨迹对应的五位置鞍圆和鞍圆误差。同四位置一样,以运动刚体点坐标
(
x
P
m
,
y
P
m
)
({{x}_{Pm}},{{y}_{Pm}})
(xPm,yPm)为自变量,对应五位置鞍圆误差
Δ
12345
{{\Delta }_{12345}}
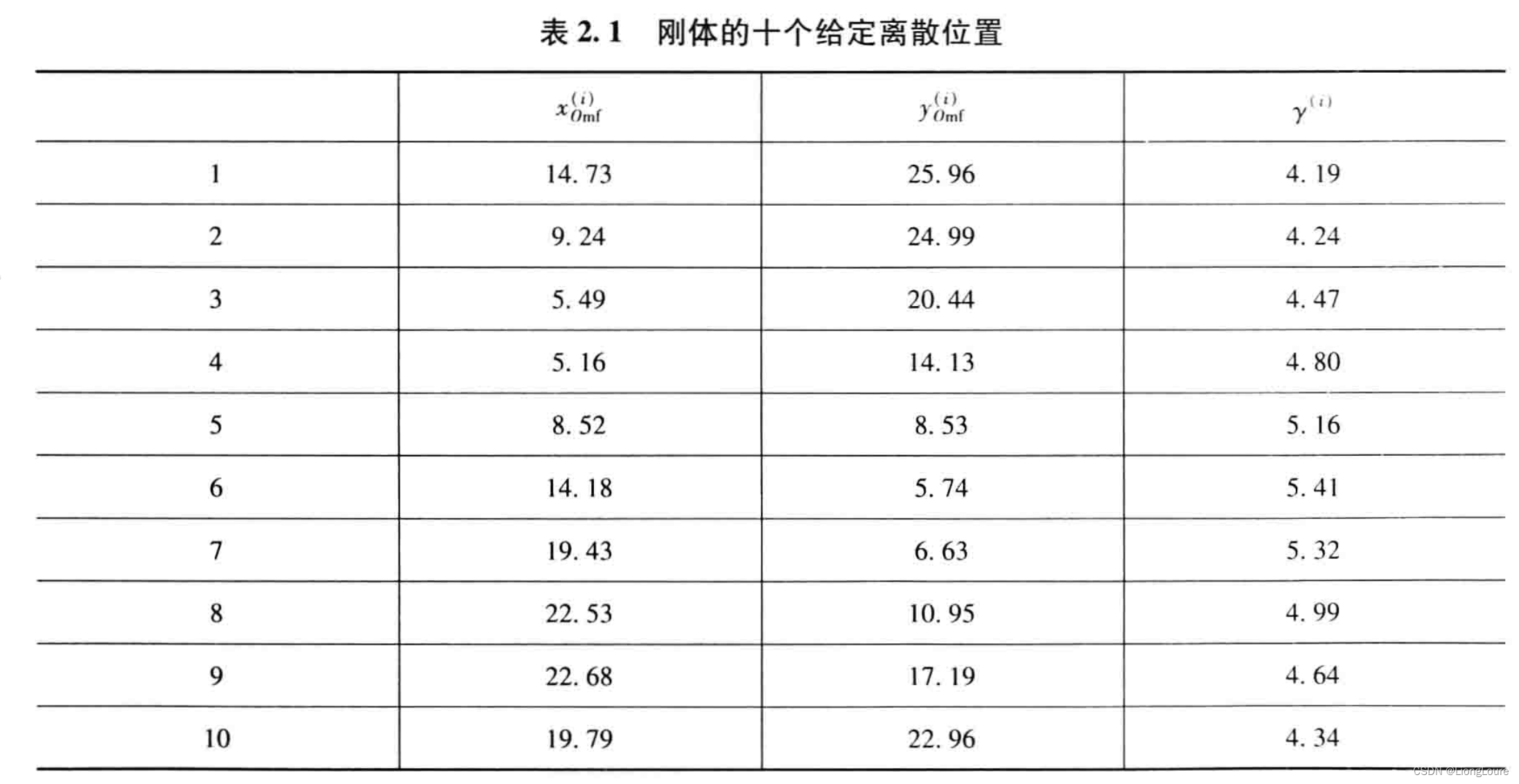
Δ12345为因变量,构造出五位置运动刚体上点-鞍圆误差曲面,并绘制出五位置鞍圆误差等高线图,如下图 所示。图中数据来源于表2.1给出的平面运动刚体十个离散位置中的前五个离散位置。
对于鞍点规划模型和数值计算而言,四位置和五位置没有区别,但从离散运动几何学角度看,探讨四位置和五位置有何联系和区别具有重要意义,可为研究多位置提供依据。
如前所述,运动刚体上P点在固定坐标系中产生离散轨迹的五个点,分别为 P ( 1 ) , P ( 2 ) , P ( 3 ) , P ( 4 ) , P ( 5 ) {{P}^{(1)}},{{P}^{(2)}},{{P}^{(3)}},{{P}^{(4)}},{{P}^{(5)}} P(1),P(2),P(3),P(4),P(5)。当采用鞍点规划模型对其进行鞍圆拟合时,五位置鞍圆也只有四个拟合特征点,对应五个位置中的四个为拟合特征位置,共有五种可能组合,即 1234 1234 1234, 1235 1235 1235、 1245 1245 1245、 1345 1345 1345和 2345 2345 2345。那么,五位置鞍圆中哪四个位置在什么时候是拟合特征位置? 五位置鞍圆如何由一种特征四位置组合变化到另一种四位置组合? 由此可以揭示四位置鞍圆和五位置鞍圆的关系。
前面已经介绍了给定四个位置时,运动刚体上点及其离散轨迹对应的鞍圆及鞍圆误差曲面;对于五位置离散运动刚体,可视为在上述四位置基础上增加第五个位置,那么,运动刚体上点 P P P对应五个离散点 P ( 1 ) ∼ P ( 5 ) {{P}^{(1)}}\sim{{P}^{(5)}} P(1)∼P(5)的轨迹,点 P ( 5 ) {{P}^{(5)}} P(5)要么是五位置鞍圆拟合特征点,要么不是,只有两种可能,现分别讨论如下。
- 1)第五个点
P
(
5
)
{{P}^{(5)}}
P(5)是离散轨迹的五位置鞍圆拟合特征点,对应第五个位置此时不是五位置鞍圆拟合位置。 如下图所示,五个离散点
P
(
1
)
∼
P
(
5
)
{{P}^{(1)}}\sim{{P}^{(5)}}
P(1)∼P(5)轨迹的五位置鞍圆由前四个位置(
1234
1234
1234)的离散轨迹点
P
(
1
)
∼
P
(
4
)
{{P}^{(1)}}\sim{{P}^{(4)}}
P(1)∼P(4)确定,或着说
P
(
1
)
∼
P
(
4
)
{{P}^{(1)}}\sim{{P}^{(4)}}
P(1)∼P(4)所确定的两个同心圆包容了第五个点,离散点
P
(
5
)
{{P}^{(5)}}
P(5)误差小于前四个离散点的四位置鞍圆误差
Δ
1234
{{\Delta }_{1234}}
Δ1234,则有
Δ
12345
=
Δ
1234
{{\Delta }_{12345}}={{\Delta }_{1234}}
Δ12345=Δ1234。所以,对于给定五个离散位置,运动刚体上存在部分点,其离散轨迹对应的五位置鞍圆由前四个离散点(
1234
1234
1234)决定。由前四位置确定鞍圆的这些点分布在运动刚体上特定区域,如上图所示
区域I中的点,鞍圆拟合位置均对应 1234 1234 1234四个位置,为 1234 1234 1234四位置鞍圆区域。
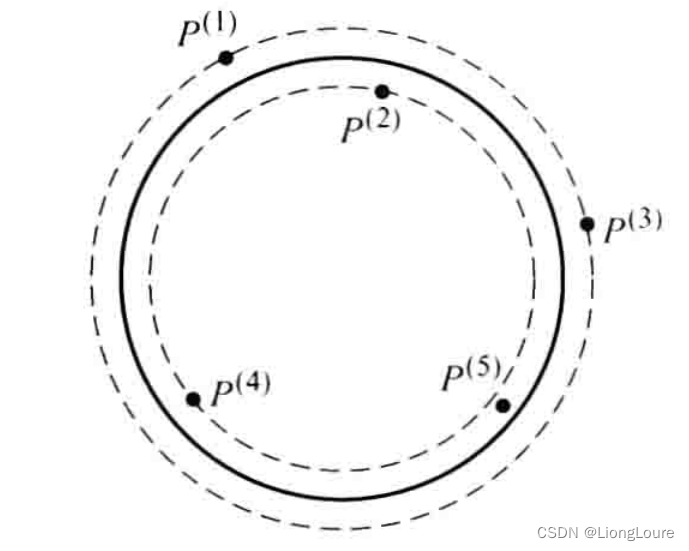
此区域还有另一种情况,五位置鞍圆由 P ( 1 ) ∼ P ( 4 ) {{P}^{(1)}}\sim{{P}^{(4)}} P(1)∼P(4)所确定,但并不是该四位置鞍圆,如下图所示。该四位置鞍圆为圆 C 1 {{C}_{1}} C1,由 P ( 1 ) P ( 3 ) − P ( 2 ) P ( 4 ) {{P}^{(1)}}{{P}^{(3)}}-{{P}^{(2)}}{{P}^{(4)}} P(1)P(3)−P(2)P(4)(确定,四位置鞍圆误差为 Δ 1234 = Δ 13 , 24 {{\Delta }_{1234}}={{\Delta }_{13,24}} Δ1234=Δ13,24;而五位置鞍圆为圆 C 2 {{C}_{2}} C2,仍由前四个位置的离散点确定,分布为 P ( 1 ) P ( 3 ) − P ( 2 ) P ( 4 ) {{P}^{(1)}}{{P}^{(3)}}-{{P}^{(2)}}{{P}^{(4)}} P(1)P(3)−P(2)P(4),五位置鞍圆误差为四位置三个分布圆中的次小误差 Δ 12345 = Δ 12 , 34 {{\Delta }_{12345}}={{\Delta }_{12,34}} Δ12345=Δ12,34,不是最小值 Δ 13 , 24 {{\Delta }_{13,24}} Δ13,24。所以,五位置鞍圆并不一定是某一个四位置鞍圆,而是四位置三个分布圆中的一个。
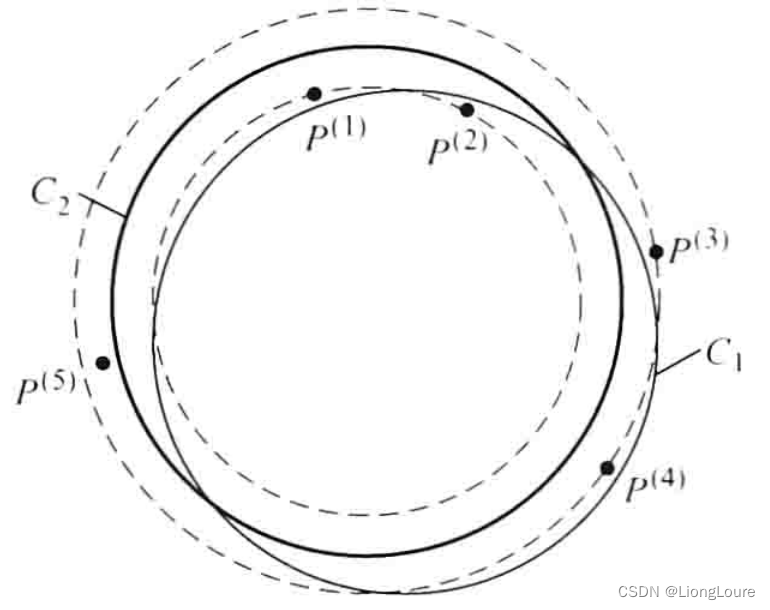
- 2)第五个点
P
(
5
)
{{P}^{(5)}}
P(5)是离散轨迹的四个鞍圆拟合特征点之一,对应第五个离散位置是鞍圆拟合位置。 那么,第五位置需和前四个位置中的三个位置共同构成鞍圆拟合四位置,有四种可能∶
1235
1235
1235、
1245
1245
1245、
1345
1345
1345和
2345
2345
2345。显然,每种四位置组合为离散运动四位置,和前述四位置(
1234
1234
1234)一样,都对应一个四位置刚体上
点-鞍圆误差十二次代数曲面。但在运动刚体上同一点 P P P处,对应离散轨迹五点和五位置鞍圆,也必为某四位置组合,或某四位置分布圆中的一个,而四种组合共有十二个分布圆,五位置鞍圆是十二个分布圆中的一个,使得五位置离散轨迹点 P ( 1 ) ∼ P ( 5 ) {{P}^{(1)}}\sim{{P}^{(5)}} P(1)∼P(5)的最大拟合误差最小。
对于所示五位置鞍圆误差曲面上的若干区域,每个区域刚体上点对应不同的四位置鞍圆的拟合特征位置,例如,区域I对应 1234 1234 1234,区域Ⅱ对应 1235 1235 1235,区域Ⅲ对应 1245 1245 1245,区域Ⅳ对应 1345 1345 1345,区域V对应 2345 2345 2345。由于离散运动刚体上点是连续的,从区域I(1234)变化到区域Ⅱ(1235)时,而边界上点同时属于两个相邻区域的点,自然应该具有两个区域的特性,则该点的离散轨迹上五个点都是拟合特征点,形成与相邻区域对应的两个鞍圆及其误差。 而按照鞍圆定义,一条轨迹只能有一个鞍圆,那么,该五点轨迹对应两个误差相同的分布圆,或者说该轨迹的鞍圆有两个解(误差相等,属于不同的分布圆),以适应相邻区域过渡。将相邻区域的鞍圆误差曲面方程联立,如 Δ 1234 = Δ 1235 {{\Delta }_{1234}}={{\Delta }_{1235}} Δ1234=Δ1235,由分布圆误差公式和四位置鞍圆误差公式解得边界曲线方程。三个或四个区域界限点处,则有该点离散轨迹的五个点对应三个误差都相等的分布圆,鞍圆有三个解。特殊地,边界点对应多个误差相等的分布圆重合(同一个分布圆)时,则此处鞍圆误差曲面可能具有新的特点,如二阶连续(相切地过渡),否则相交;相切过渡边界为三次代数曲线。有关五位置鞍圆误差曲面及其边界曲线的代数与几何性质还需要进一步深入研究。
如前所述,五位置的鞍圆及其误差曲面在理论上可分解为五个四位置的分布圆误差曲面的组合,即多片(区域)十二次代数曲面组合,属于高阶代数曲面,存在多个峰谷;而等高线则跨越不同的四位置点区域,仅表明鞍圆误差相等。从整体上比较五位置与四位置的鞍圆误差曲面,四位置存在一条误差为零的等高线——圆点曲线,相当于河谷;而五位置的等高线则没有,仅有鞍圆误差为零的若干个误差较小的谷底点——Burmester点,相当于把河流变成河床,露出几潭水的河谷。因为在多片(区域)代数曲面组合鞍圆误差曲面时,同一点对应四位置鞍圆误差大的代替误差小的,所以,总体上说,五位置的鞍圆误差曲面要比四位置的数值大,而峰谷少。
2.3.5 多位置鞍圆
由上述讨论可知,对于五位置运动刚体,运动刚体上点在固定坐标系中的离散轨迹对应鞍圆及其误差是由相关的四位置体现的,运动刚体上所有点的鞍圆误差曲面也是由相关四位置对应十二次代数误差曲面的分片组合而成的;对于多位置(五个以上)运动刚体上的点,依据鞍点规划(最大误差最小)的误差评价模型,其离散轨迹曲线与圆的近似程度由该曲线上四个拟合特征点体现,对应四个拟合位置,无论给定多少个位置都是如此,即多位置可分解为相关四位置的组合。因此,给定再多位置的运动刚体,其离散点轨迹的鞍圆及其误差性质与五位置的类似,没有本质区别,仅仅对应的四位置组合更多,按组合有 C n 4 C_{n}^{4} Cn4个区域,在运动刚体上对应的四位置点区域也只是更多些而已,无须再述。对于表2.1中给定的平面运动刚体十个离散位置,刚体平面上点的鞍圆误差曲面及等高线如下图所示。
当运动刚体的位置数目趋于无穷——无限接近位置时,运动刚体上点的轨迹趋于连续曲线,如2.2所述,曲线与圆的接近程度仍然由四个拟合特征点确定,对应运动刚体四个拟合位置。运动刚体上的点连续变化,其轨迹曲线均对应四个拟合特征点,运动刚体上没有像离散位置那样的位置点区域。
在经典的有限分离位置运动几何学中,借助转动极讨论了五位置以下运动刚体上相关点共圆的若干规律,形成了Burmester理论;其实,刚体平面运动存在不变量,是刚体运动变换矩阵的特征向量和特征值,反映了运动的本质,如经典理论中的转动极对应两位置的回转轴;对于多个位置平面离散运动,利用鞍点规划建立四位置相关点共圆模型,猜想也应该存在类似两位置转动极那样的不变量,扩展了平面离散运动几何学内涵,从少位置到多位置,从局部到整体,揭示了平面离散运动刚体上点对应的鞍圆大小、圆心位置和误差分布等,是刚体运动点轨迹与圆比较的表现形式。将其推广到其他曲线比较,以适应机构离散运动几何学研究的需要,如圆对应平面二副杆R-R的约束曲线,而直线对应平面二副杆P-R的约束曲线。其他约束曲线与约束曲面的比较研究与探索,如空间运动的有限螺旋运动与共约束曲面也仅限于少位置,在第5章和第7章将分别介绍球面与空间离散运动几何学与机构鞍点综合。