👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
本文主要介绍了一种基于蚁群算法的时延Petri网(ACOTPN)路径规划算法,它是根据蚁群算法的原理和时延库所Petri网的路径规划原理合成的一种新算法。当ACOTPN运行时,蚂蚁在网中的变迁行走并在变迁与变迁之间留下信息素,在遍历同时不仅更新变迁序列,而且会更新网标识,反过来通过判断网标识是否处于终止标识来决定蚂蚁遍历是否结束。
道路交通作为当今社会生产生活的重要一环,保障城市交通道路的安全畅通,是实现城市人民生活稳步发展的一个先决条件,更是保障社会进步至关重要的一部分。随着经济生活的不断发展,城市交通面对着愈演愈烈的矛盾冲突,一方面是城市发展中城市化进程需求的不断提高,另一方面是大中型城市内机动车密度提升所带来的的道路拥堵、环境污染等问题,能否找到合理平衡交通运输中的矛盾点已成为社会良性发展的关键因素。因此,对于路径规划问题的研究具有很重要的理论意义和现实意义。为了满足在车辆行驶过程中算法计算的高效性,要利用车辆接收到的信息进行实时重计算求出最短时间路径。经典的最短时间路径算法有其局限性,例如在道路情景复杂时对路径规划进行实时计算会出现性能不佳的情况,不同的参数选择会导致不同的结果等。为了更好地解决这些问题,本文利用时延Petri网对城市交通路径进行建模,以资源库所中托肯数的变化来表示城市交通路径的拥挤程度,将复杂的城市交通用简洁的建模方式来表示,从可达图和时延Petri网结构出发分别提出两种最短时间路径规划算法,结合实时返回的道路拥堵信息,为车辆寻求一条最短时间路径。时延Petri网模型作为一类有力的数学工具,广泛应用于交通运输的建模、分析和控制,可以用来分析系统的性能指标,解决实时的路径规划等问题。本文致力于研究以时延Petri网建模的最短时间路径规划问题,主要内容如下:1.将局部城市交通路径利用时延Petri网进行建模,将库所作为道路路径,库所中的时延因素即为路径的通行时间,库所中的托肯作为道路上的车辆,触发变迁代表选择路径,以资源库所中托肯数的变化来表示道路的拥挤程度。2.根据模型计算它的可达图,从可达图出发,优化A*算法的启发式搜索函数,对车辆的最短时间路径进行搜索计算,以资源库所中的托肯数目实时返回路径的信息,使用合适的拥堵粘滞因子,动态变化通行时间,最终为目标车辆选择出一条从初始位置到目标位置的最短时间路径,并得到时延Petri网的最短时间序列,通过实例分析验证算法的可行性和有效性。3.在Petri网模型基础上,从时延Petri网结构出发,利用提出的启发式搜索函数对每辆车进行路径规划,实现将车辆完全分布在Petri网上,并找到各自的最短时间路径。最后将模型转化为图的形式,通过MATLAB编程实现实例的模拟仿真,验证算法的正确性。
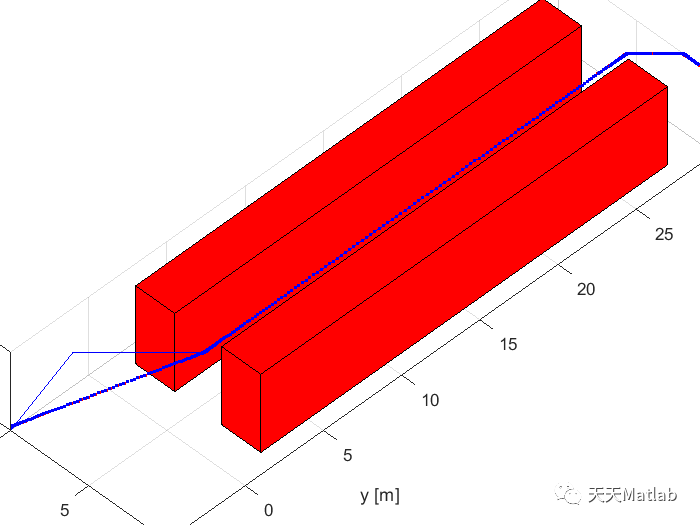
📚2 运行结果
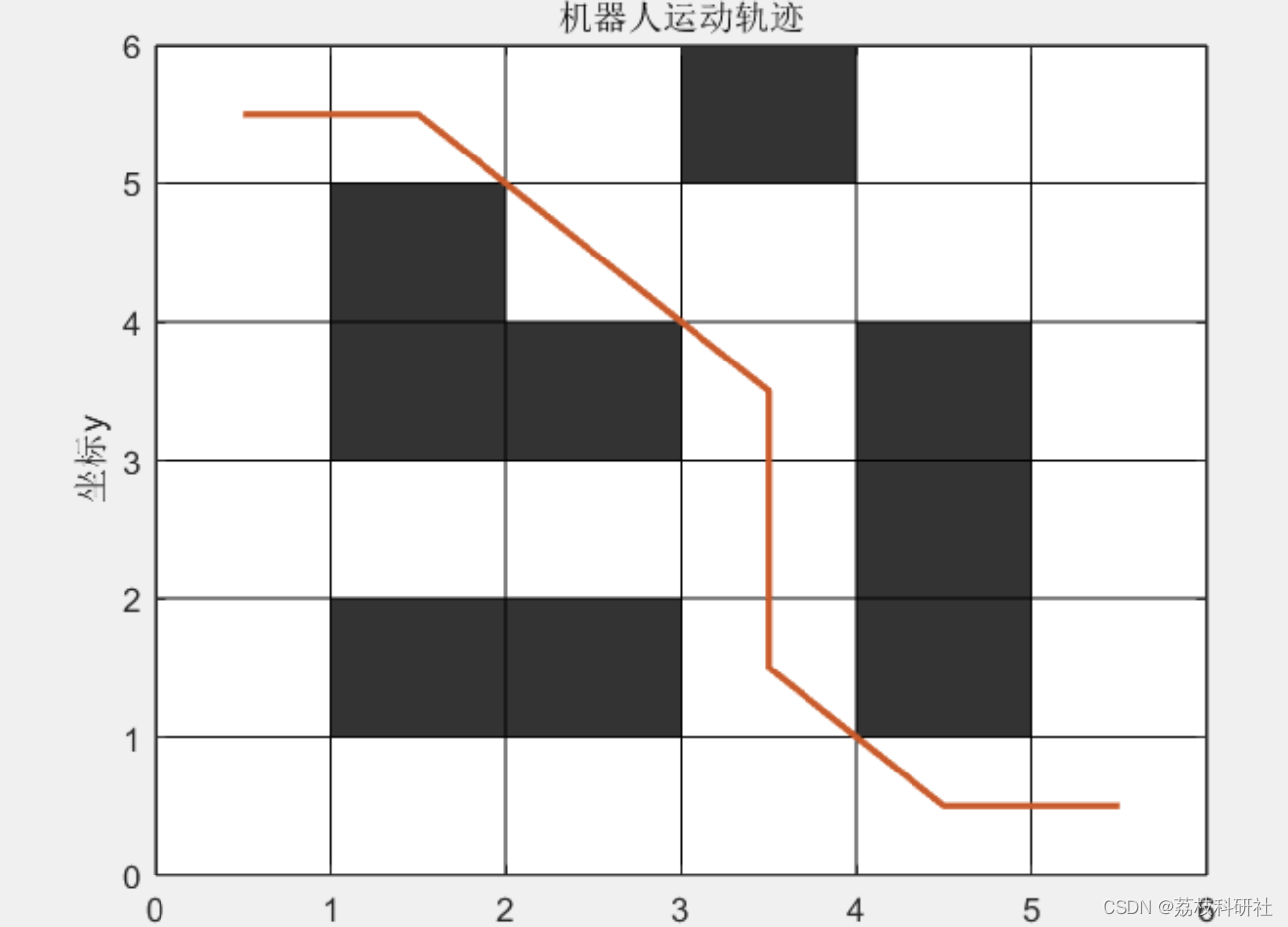
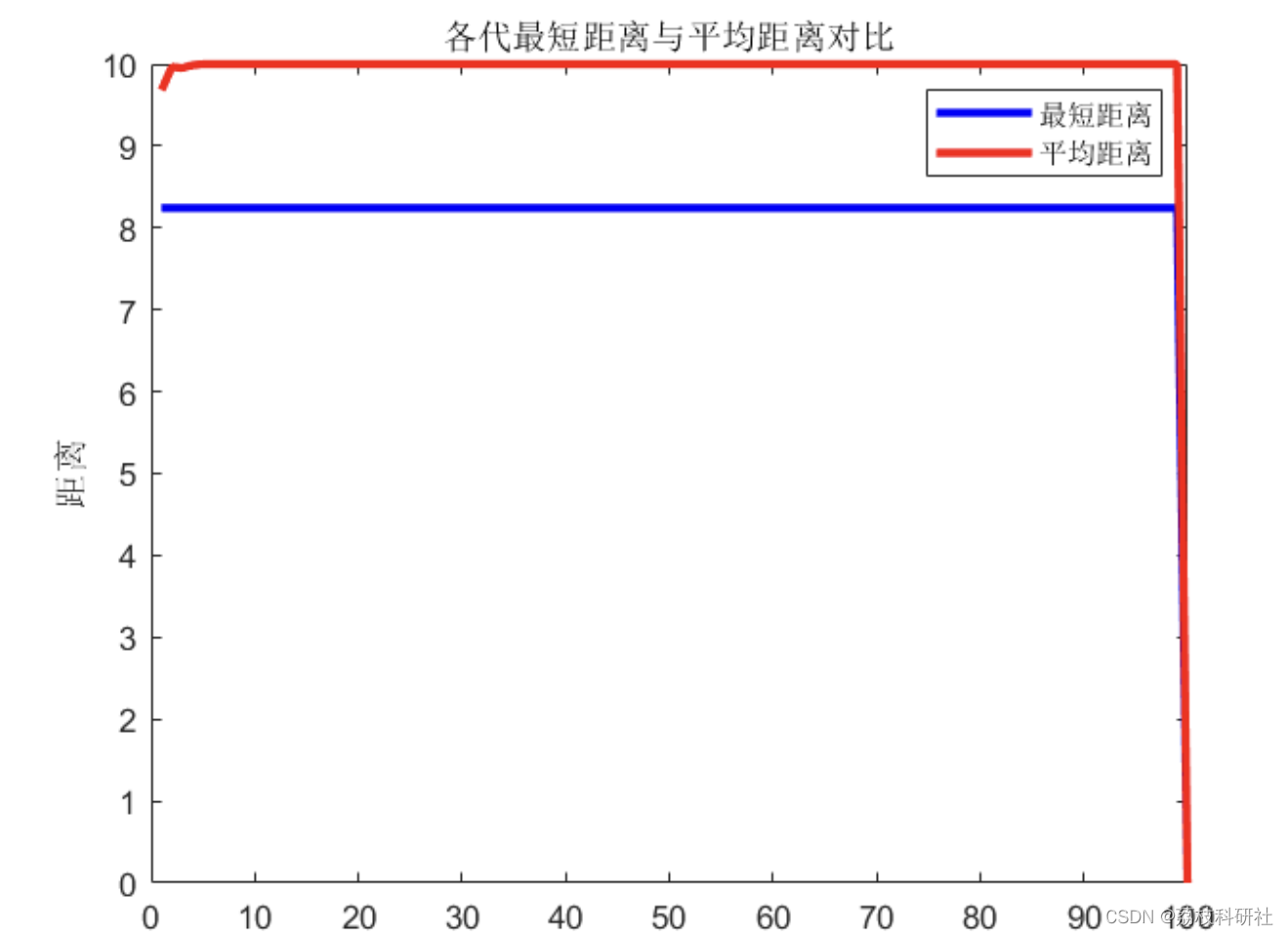
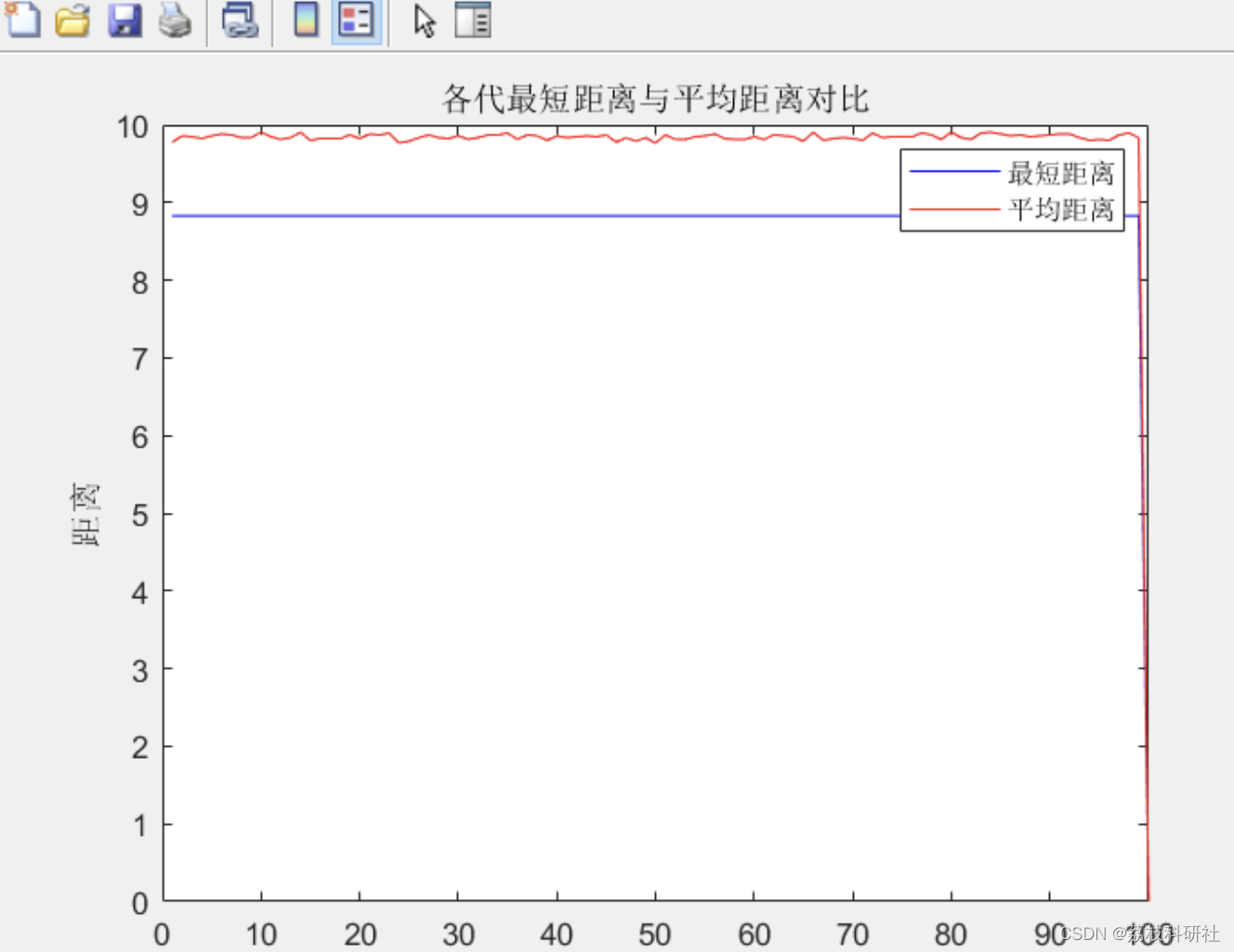
部分代码:
%% 始末节点%%
node_start=1;
node_end=[34,36];
%%% 蚁群定义%%%%%
m=50; % 蚂蚁数量
n=size(nodes_data,1); % 节点数量
alpha=1; % 信息素重要程度因子
beta=5; % 启发函数重要程度因子
Rho=0.5; % 信息素挥发因子
Q=1; % 信息素增加强度系数
%%迭代过程初始化定义%%%%
iter=1; % 迭代次数初值
iter_max=500; % 最大迭代次数
Route_best=cell(iter_max,1); % 各代最佳路径
Length_best=zeros(iter_max,1); % 各代最佳路径长度
Length_ave=zeros(iter_max,1); % 各代路径平均长度
Place_best=cell(iter_max,1); % 各代最佳路径访问的库所
%%将信息素、挥发因子一并放入nodes_data中%%%%%
Delta_Tau_initial=nodes_data(:,1:2);
for i=1:size(nodes_data,1)
nodes_data{i,5}=ones(1,length(nodes_data{i,3})); % 初始信息素均设置为1
nodes_data{i,6}=1./nodes_data{i,3}; % 启发函数设置为距离的倒数
Delta_Tau_initial{i,3}=zeros(1,length(nodes_data{i,3})); % 信息素变化量均为0
end
%% 迭代寻找最佳路径%%%
while iter<iter_max
route=cell(0);
place=cell(0);
for i=1:m % 逐个蚂蚁进路径选择
neighbor_allow=cell(0);
node_step=node_start;
path=node_step;
path_M = 0;
if node_step==node_start
marking=M_1;
else
marking=nodes_data{node_step,4};
%% 始末节点%%
node_start=1;
node_end=[34,36];
%%% 蚁群定义%%%%%
m=50; % 蚂蚁数量
n=size(nodes_data,1); % 节点数量
alpha=1; % 信息素重要程度因子
beta=5; % 启发函数重要程度因子
Rho=0.5; % 信息素挥发因子
Q=1; % 信息素增加强度系数
%%迭代过程初始化定义%%%%
iter=1; % 迭代次数初值
iter_max=500; % 最大迭代次数
Route_best=cell(iter_max,1); % 各代最佳路径
Length_best=zeros(iter_max,1); % 各代最佳路径长度
Length_ave=zeros(iter_max,1); % 各代路径平均长度
Place_best=cell(iter_max,1); % 各代最佳路径访问的库所
%%将信息素、挥发因子一并放入nodes_data中%%%%%
Delta_Tau_initial=nodes_data(:,1:2);
for i=1:size(nodes_data,1)
nodes_data{i,5}=ones(1,length(nodes_data{i,3})); % 初始信息素均设置为1
nodes_data{i,6}=1./nodes_data{i,3}; % 启发函数设置为距离的倒数
Delta_Tau_initial{i,3}=zeros(1,length(nodes_data{i,3})); % 信息素变化量均为0
end
%% 迭代寻找最佳路径%%%
while iter<iter_max
route=cell(0);
place=cell(0);
for i=1:m % 逐个蚂蚁进路径选择
neighbor_allow=cell(0);
node_step=node_start;
path=node_step;
path_M = 0;
if node_step==node_start
marking=M_1;
else
marking=nodes_data{node_step,4};
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]王荣. 基于时延Petri网的最短时间路径规划[D].西安电子科技大学,2020.DOI:10.27389/d.cnki.gxadu.2020.001577.