一.拟合优度度量（可决系数）

拟合度指回归直线与样本数据趋势的吻合程度。

拟合优度检验:对样本回归直线与样本观测值之间拟合程度的检验,。
度量拟合优度的指标:可决系数(判定系数) R*2

1.1总离差平方和的分解

已知由一组样本观测值(Xi,Yi),i=l,2…,n 得到如下样本回归直线:

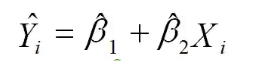
而Y的第i个观测值与样本均值的离差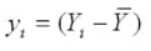可分解为两部分之和

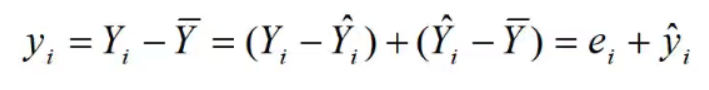
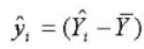是样本回归拟合值与观测值的平均值之差,可认为是由回归直线解释的部分。

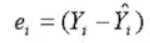是实际观测值与回归拟合值之差,是回归直线不能解释的部分。

如果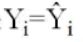即实际观测值落在样本回归"线"上,则拟合最好。
可认为,"离差"全部来自回归线,而与"残差"无关。

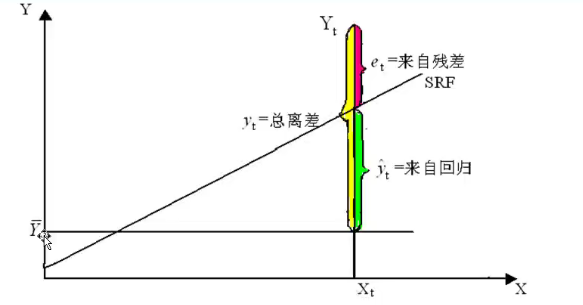
对于所有样本点,则需考虑这些点与样本均值离差的平方和,可以证明:

1.2 TSS=ESS+RSS

Y的观测值围绕其均值的总离差(total variation)可分解为两部分:一部分来自回归线(ESS),另一部分则来自随机势力(RSS)。

在给定样本中，TSS不变，如果实际观测点离样本回归线越近， 则ESS在TSS中占的比重越大， 因此拟合优度：回归平方和ESS/Y的总离差TSS

1.3 红酒数据集实例R2_score实现代码

SSE是残差平方和，SST是总利差平方和
R2通俗地理解为使用均值作为误差基准，看预测误差是否大于或者小于均值基准误差。
R2_score = 1，样本中预测值和真实值完全相等，没有任何误差，表示回归分析中自变量对因变量的解释越好。
R2_score = 0。此时分子等于分母，样本的每项预测值都等于均值。
根据公式，我们可以写出R2_score实现代码

1.事前准备，使用红酒数据集：

from sklearn.model_selection import train_test_split
from sklearn import linear_model
from sklearn.datasets import load_wine
wine = load_wine()
X = wine.data
y = wine.target

2.切分数据集：使用前百分之30。

wine_X_train, wine_X_test, wine_y_train, wine_y_test = train_test_split(X, y, test_size=0.3, random_state=0)

3.每个测试集的所预测的各个类别的概率

y_predict=model.predict(wine_X_test)

4.保存

train_score,test_score=[],[]
train_score.append(model.score(wine_X_train, wine_y_train))
test_score.append(model.score(wine_X_test, wine_y_test))

5.引入R2_score

from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error

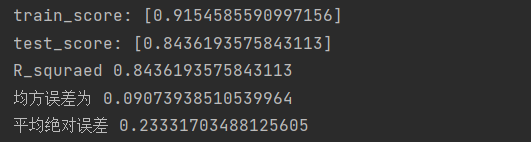
6.结果如下

print("train_score:",train_score)
print("test_score:",test_score)
print("R_squraed",r2_score(wine_y_test,y_predict))
print("均方误差为",mean_squared_error(wine_y_test,y_predict))
print("平均绝对误差",mean_absolute_error(wine_y_test,y_predict))

二. 梯度下降

2.1 损失函数直观图(单特征/变量举例)

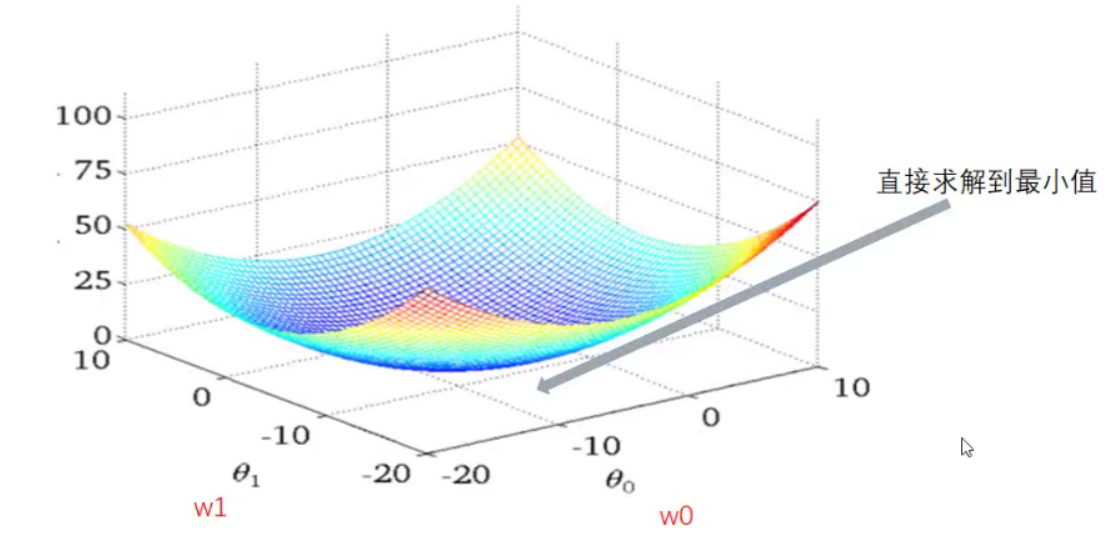
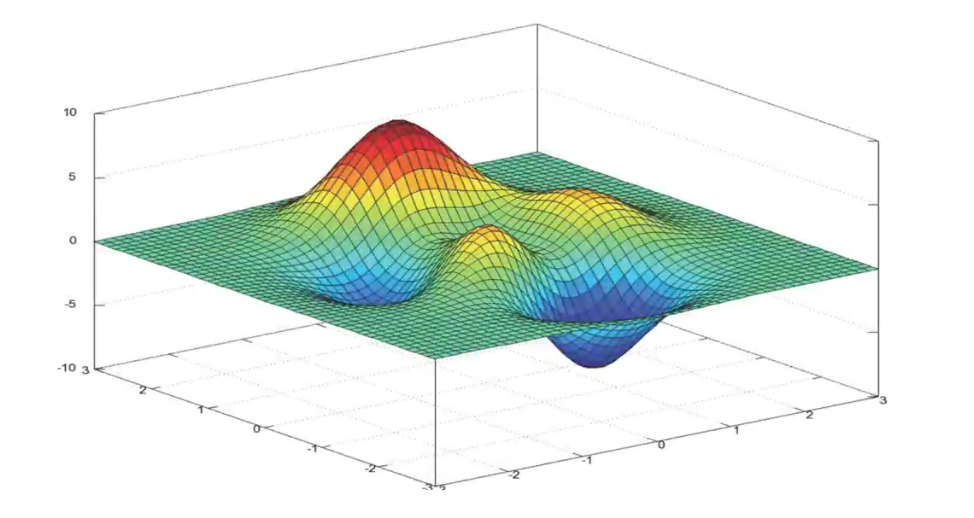
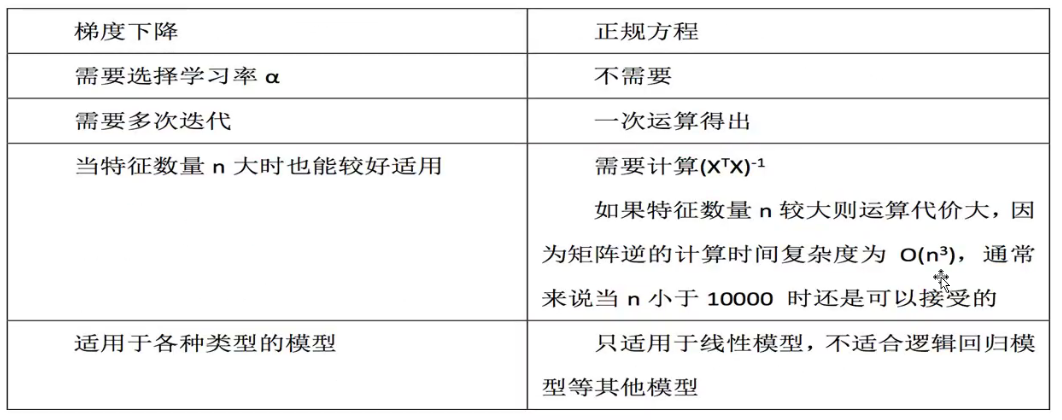
2.2 梯度下降和正规方程的区别

2.3 线性回归模型——梯度下降 （红酒数据集）

1.事前准备，使用红酒数据集：

from sklearn.model_selection import train_test_split
from sklearn import linear_model
from sklearn.datasets import load_wine
wine = load_wine()
X = wine.data
y = wine.target

2.手动进行按列归一化：

wind_X=X.copy()

for i in range(13):
    columu_X = X[:, i]
    wind_X[:, i]=(columu_X-columu_X.mean())/columu_X.std()

3.切分数据集，取前百分之30。

wine_X_train, wine_X_test, wine_y_train, wine_y_test = train_test_split(wind_X, y, test_size=0.3, random_state=0)

4.随机梯度模型：SGDRegressor

model = linear_model.SGDRegressor()

5.输出测试集和训练集分数：

model.fit(wine_X_train,wine_y_train)
print("training score: ", model.score(wine_X_train,wine_y_train))
print("test score: ", model.score(wine_X_test,wine_y_test))

6.结果如下：

2.4 sklearn线性回归正规方程与梯度下降API

1.sklearn.linear_model.LinearRearession()

• 普通最小二乘线性回归

• 正规方程

• coef：回归系数

2.linear_model.SGDRegressor()

• 通过使用SGD最小化线性模型

• 梯度下降

• coef:回归系数

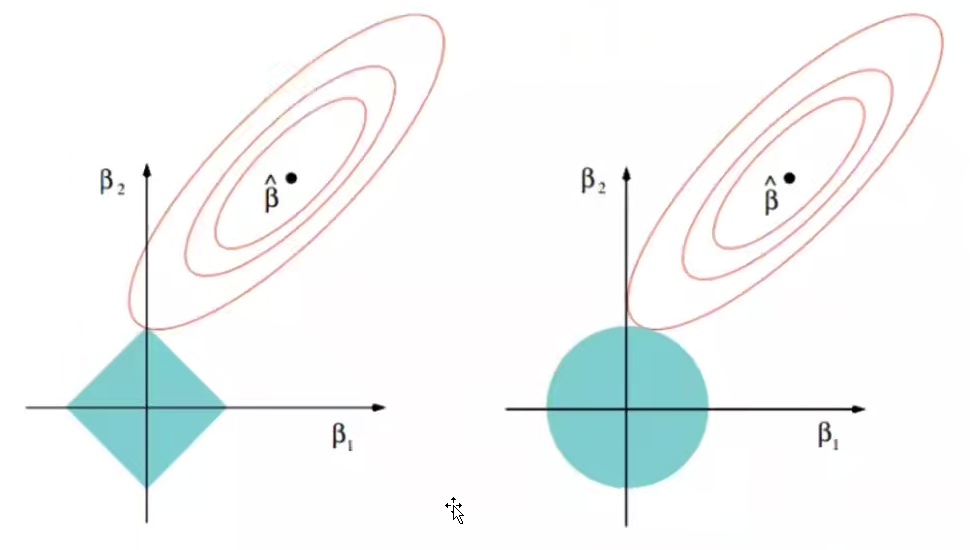
2.5 岭回归

岭回归(Ridge Regression)是种改良的最小二乘法，其通过放弃最小二乘法的无偏性，以损失部分信息为代价来寻找效果稍差但回归系数更符合实际情况的模型方程该模型求解的回归模型的损失函数为线性最小二乘函数，正则化采用L2-范数。称为岭回归。

岭回归（Ridge Regression)与套索回归（Lasso Regression)两个算法不是为了提升模型表现，而是为了修复漏洞而设计的。

1.使用岭回归：

model = linear_model.Ridge()

2.上面代码模型使用岭回归之后，重新运行：

from sklearn.model_selection import train_test_split
from sklearn import linear_model
from sklearn.datasets import load_wine
wine = load_wine()
X = wine.data
y = wine.target


wine_X_train, wine_X_test, wine_y_train, wine_y_test = train_test_split(X, y, test_size=0.3, random_state=0)
model = linear_model.Ridge()
# model = linear_model.Lasso(alpha=0.1)
train_score,test_score=[],[]
model.fit(wine_X_train,wine_y_train)
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
y_predict=model.predict(wine_X_test)
train_score.append(model.score(wine_X_train, wine_y_train))
test_score.append(model.score(wine_X_test, wine_y_test))

print("train_score:",train_score)
print("test_score:",test_score)
print("R_squraed",r2_score(wine_y_test,y_predict))
print("均方误差为",mean_squared_error(wine_y_test,y_predict))
print("平均绝对误差",mean_absolute_error(wine_y_test,y_predict))

3.得到以下结果：

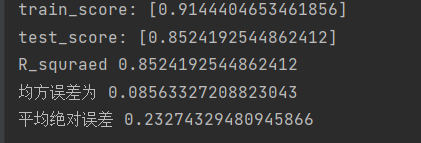
2.6 Ridge Regression

正则化项是参数的L2范数时，回归方法就叫做岭回归。因为权重系数随lambda变化呈山脊状，等于零时为最小二乘。相应损失函数：

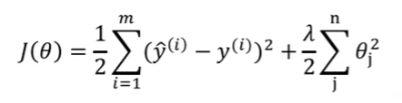
2.7 岭迹图

引入依赖包：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

数据处理

def ridgeCalc(dataSet):
    xMat = np.mat(dataSet.iloc[:, :-1].values)
    yMat = np.mat(dataSet.iloc[:, -1].values).T
    yMean = np.mean(yMat, axis = 0)
    yMat = yMat - yMean
    xMeans = np.mean(xMat, axis = 0)
    xVar = np.var(xMat,axis = 0)
    xMat = (xMat - xMeans)/xVar
    numTestPts = 30
    wMat = np.zeros((numTestPts,xMat.shape[1]))
    for i in range(numTestPts):
        ws = ridgeRegres(dataSet, np.exp(i-10))
        wMat[i,:]=ws.T
    return wMat

手动计算岭回归：

def ridgeRegres(dataSet, lam=0.2):
    xMat = np.mat(dataSet.iloc[:, :-1].values)
    yMat = np.mat(dataSet.iloc[:, -1].values).T
    xTx = xMat.T * xMat
    denom = xTx + np.eye(xMat.shape[1])*lam
    ws = denom.I * (xMat.T * yMat)
    return ws

将其进行可视化输出：

ridgeWeights = ridgeCalc(df)
plt.plot(ridgeWeights)
plt.xlabel('log(lambda)')
plt.ylabel('weights')
plt.show()

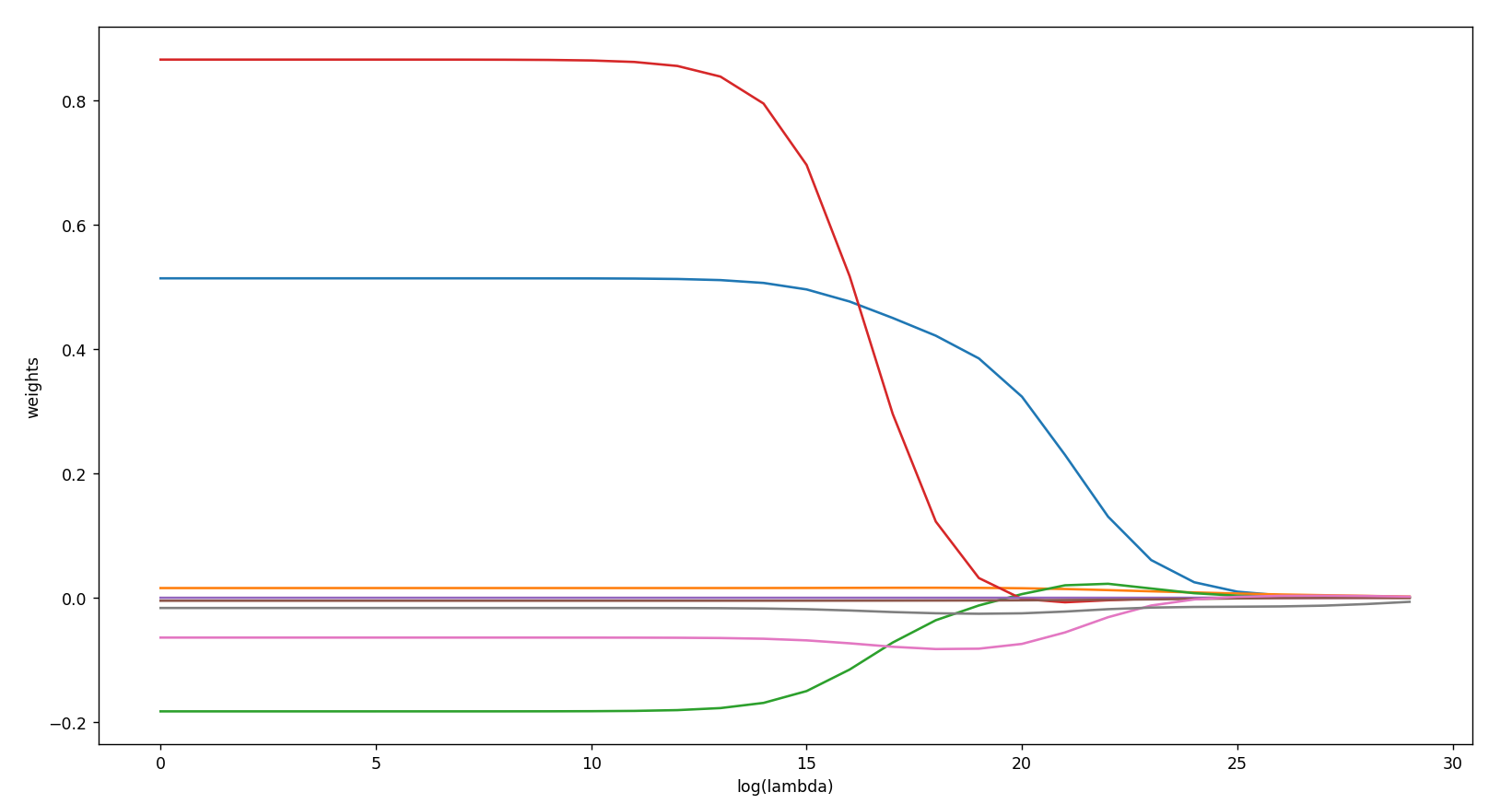
本次程序运行截图，岭回归：